Diyelim ki bir seçim arifesindesiniz; örneğin bir ev alacaksınız ve seçenekleri sıraladınız. Gezdiğiniz 3. evin ardından kararınızı vermiş gibisiniz. Sonucunda bu ev tüm beklentilerinizi neredeyse karşılıyor. Ertesi gün anlaşmayı yapmaya hazırsınız. Ancak akşam olduğunda aklınıza bir şey takıldı. Ya listenizdeki bir sonraki ev, almayı planladığınızdan daha iyiyse?

Aynı durum iş değiştirme ve hatta ikili ilişkilerinizde de karşınıza çıkacaktır. Bu durumda matematik ve psikoloji arasında köprü kuran bir problem olan optimal durma problemini ve beraberinde yüzde 37 kuralını bilmek işinize yarayabilir.
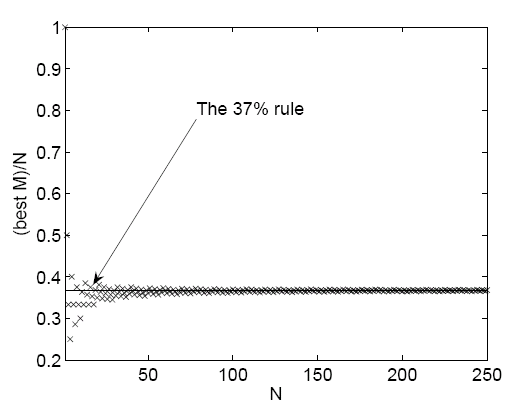
Yüzde 37 kuralı bir karar verirken toplam seçenek grubunuzun % 37’sine bakmanızı ve baktıklarınızdan sonra gelen en iyi seçenekte karar kılmanız gerektiğini söyler. Yani eğer 100 tane seçeneğiniz varsa 37 tanesini değerlendirdikten sonra daha fazlasına bakarak zaman kaybetmeden kararınızı veriniz. Çünkü muhtemelen en doğru seçenek budur.
Yüzde 37 Kuralı Ve Sekreter Problemi
%37 kuralının ortaya çıkışı sekreter problemi denilen ünlü bir matematik problemine dayanıyor. Bu problemde kısaca şu şekildedir. Bir şirketiniz var ve işlerinizin yoğunluğundan dolayı yardımcı bir sekreter almanız gerekiyor.
Başvurular yoğun, siz de adaylar arasından en iyisini işe almak istiyorsunuz. Bunun için adaylar ile tek tek görüşüyorsunuz. Eğer bir adayı reddederseniz onu tekrar görüşmeye çağıramıyorsunuz çünkü başka bir iş bulmuş olma ihtimali yüksek. Peki bu durumda en iyi sekreteri işe alma olasılığınızı en yükseğe çıkarmak için adayların kaçıyla görüştükten sonra karar vermelisiniz?
Matematikçiler bu problem için en ideal çözümün 1/e oranı olduğunu bulmuşlardır. Hesap makinesi ile hesaplarsanız 1/e sayısının %37’ye çok yakın bir sayı olduğunu görebilirsiniz. ( Olasılık hesaplamalarını merak ederseniz yazının sonundaki bağlantılara göz atabilirsiniz)
Matematik Duygusal İlişkilerde de İşinizi Kolaylaştırabilir!
Şimdi bu problemi biraz magazin boyutuna taşıyalım ve aynı oranı matematiksel anlamda ideal evlilik yaşını bulmakta kullanalım. Kulağa biraz duygusuz gelse de sayılar pek yalan söylemez. Diyelim ki toplum kurallarına uygun yaşamayı seven birisiniz. O zaman size dayatılan genelde 18-40 yaş arasında evlenmenizdir. Yani 22 sene içinde bir seçim yapmak zorundasınız.
Bu 22 sayısının %37 sini alıp 18’e eklerseniz 26,14 yapar. Bunun anlamı şu en ideal seçim yapacağınız yaş 26 yı biraz geçince. Bu yaştan önce karşılaşılan romantik partnerler arasında muhtemelen çok iyi olanlar da var ama teoriye göre bu zamandan sonra iyi opsiyonlar giderek ‘bulunamaz’ veya ‘uygun değil’ hale geliyorlar. Bu da mükemmel eş bulma şansını düşürüyor.
Evlilik Yaşı Formülü

Ne diyelim elbette bir teori ancak bu bilgiyi destekleyen başka bir çalışma daha var. New South Wales Üniversitesi tarafından yürütülen çalışmanın sonuçlarına göre, evlenmek için en mükemmel yaş, 4 maddeli birkaç basit matematik işlemiyle bulunabiliyor. Çalışmalar sırasında formülü uygulayanların yüzde 40’ında doğru sonuç alındığı belirtildi.
- Evlenmek istediğiniz en geç yaşı yazın ve bunu “n” harfiyle adlandırın. Örneğin n=39
- İlk kez bir partneriniz için “Bu kişiyle evlenirim” dediğiniz yaşı yazın ve bunu “p” harfiyle adlandırın. Örneğin p=20
- Şimdi n’den p’yi çıkartın ve sonucu 0.368 ile çarpın. (39-20) x 0,368 Sonuç: 6.992
- Elde ettiğiniz sayıyı, p’ye ekleyin. 20 + 6.992 Sonuç yaklaşık olarak 27
- Bu arada 0,368 katsayısının hemen hemen %37 ye denk geldiğine dikkat edelim. Var bir hikmet bu 37’de.
Yüzde 37 kuralı vereceğimiz çoğu kararda bize en uygun çözümü sunar
Bahsettiğimiz gibi gündelik hayatta %37 kuralını uygulayabileceğimiz birçok problem ile karşılaşırız. Fakat her zaman bu stratejiyi uygulamamıza gerek olmayabilir. Bazı durumlarda önceden edindiğimiz bilgileri uygulamak daha iyi bir strateji olabilir.
Örneğin daha önceden 3 yıl yaşadığınız bir şehre kısa süreliğine geri geldiğinizi varsayalım. Bir öğlen vakti karnınız acıktı ve bir restorana gitmeye karar verdiniz. 3 yıl bu şehirde yaşadığınız için elbette ki bir favori restoranınız var.
Peki, bu durumda yeni bir şeyler mi deneyeceksiniz yoksa favori restoranınıza mı gideceksiniz? Bu durumdaki en ideal çözüm favori restoranınıza gitmektir. Şehirden kısa bir süre sonra ayrılacağınız için yeni şeyler deneyerek veri toplamak anlamsızdır.
Ev bulmak, birini işe almak gibi birçok problemde %37 kuralını strateji olarak kullanabilirsiniz. Matematik size mükemmel neticeyi garantilemez. Fakat uygulayabileceğiniz en iyi strateji de budur. Göz atmak isterseniz: Yem Etkisi: Üçüncü Seçeneğin Varlığı Seçimlerimizi Nasıl Etkiler?
Kaynaklar ve ileri okumalar:
- A mathematical theory says the perfect age to get married is 26, yayınlanma tarihi: 30 Ocak 2020; Bağlantı: http://www.businessinsider.com
- Secretary problem; Bağlantı: https://en.wikipedia.org
- How many people should you date before settling down? Follow the 37% rule; yayınlanma tarihi: 21 Nisan 2022; Bağlantı: https://bigthink.com/
- Matematiksel hesaplamalar için: Strategic dating: The 37% rule; Yayınlanma tarihi: 1 Mart 2017; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel



