Bilgisayarlar son derece hızlı bir biçimde değişmeye devam ediyor. Ancak tüm değişikliklere rağmen değişmeyen tek şey matematik altyapıları. Biz görmesek de arka planda hala sıfırlar ve birler çalışıyor. İlk günden beri, karmaşık verileri anlamak için, bilgisayarınızın bunları ikili sayı sistemine çevirmesi gerekiyor.

Muhtemelen 10 tabanına yani onluk sayı sistemine aşinasınızdır. Onluk sayı sistemi 0 ile 9 arasında değişen on basamaktan yararlanır. Bu sayı sisteminde her basamak bir öncekinden on kat daha fazla değerdedir (1, 10, 100, vb.).
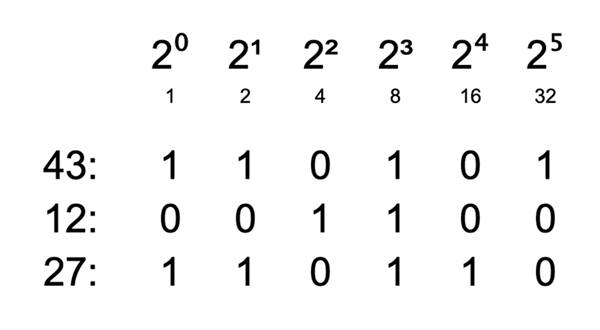
İkili sayı sistemi için de durum aslında benzerdir. Her rakam bir öncekinden iki kat daha değerlidir. İkili sayı sisteminde ilk rakam ondalık sisteme göre düşünürsek 1 değerindedir. İkinci rakam 2, üçüncü rakam 4, dördüncü 8 biçiminde devam eder. Bu sayıların hepsini toplamak da bize ikilik sistemdeki sayının onluk sistemdeki karşılığını verir. Örnekleri aşağıda görebilirsiniz.
İkili Sayı Sistemi İle Nasıl Tanıştık?
İkilik düzenin çıkışı antik çağlara uzanır, fakat bu düzeni detaylı olarak incelediğini bildiğimiz ilk kişi Gottfried Leibniz’tir. Kendisi Evet – hayır, açık – kapalı gibi hayatın ve tüm düşüncelerin ikili önermelere indirgenebileceğini düşünürdü. Sonrasında sayıları birler ve sıfırlardan oluşan, sonu gelmeyecek gibi gözüken listeler olarak yazmaya başladı.
İkilik düzenin “açık-kapalı” mantığı, birkaç yıl sonra Fransız bir ipek dokuyucusu mucit olan Joseph Jacquard’ın dikkatini çekti. Sonunda dokuma tezgahlarında bir yenilik yapmaya karar verdi. Geliştirdiği delikli kartlar ile gelecekte bilgisayar devrimine yol açacak kişilerden biri oldu. Ama 0 ve 1’in müthiş gücünü tam olarak anlayışımızı George Boole’a borçluyuz.

G. Boole (1815-1864) Mathematical Analysis of Logic (1847) adlı kitabında, mantığın metafizikten çok matematiğin bir dalı olduğunu öne sürerek, sembolik mantığı ortaya attı. Sonrasında da insan düşünce mantığını belli işlem operatörleri ile göstererek, mantıksal düşünme işlemlerini sembolleştirdi. Boole mantığı, oldukça az sayıda beklenmedik şeyin bit ve bayt olarak haritalanmasına izin verir.

Bilgisayarlar Bilgiyi Nasıl Ölçer?
Bilgisayarınızdaki her sayı bir elektrik sinyalidir ve bilgisayarların ilk zamanlarında elektrik sinyallerini çok hassas bir şekilde ölçmek ve kontrol etmek çok daha zordu. Yalnızca negatif yük ile temsil edilen “açık” durum ile pozitif bir yük ile temsil edilen “kapalı” durum arasında ayrım yapmak daha mantıklıydı. Bu nedenle, ilk oda büyüklüğündeki bilgisayarlar, sistemlerini oluşturmak için ikili sistemi kullandılar.
Programlar, bilgisayarın çalışması ve belli komutları yerine getirmesi için insanlar tarafından oluşturulan mantık algoritmalarıdır. Programlardaki komut dizileri, ikili sayı sistemine göre kodlanırlar. Bu ikili sistem mantık devrelerinde 0=yanlış, 1=doğru, ya da bir elektrik devresinde 0=elektrik akımı yok, 1=akım var anlamına gelir.

PC’de verilerin ölçülmesinde farklı terimler kullanılır. “Bit” en küçük veri elemanıdır. Temelde ikili sayı sistemindeki rakamları içerir, yalnızca 0 ve 1 değerini alırlar. “Byte” ise sayısal kodlamada kullanılan ve anlamlı bilgi içerebilen en küçük parçadır. Her bir byte 8 bit’ten oluşur. Örneğin, S harfi 0011 0111 ile temsil edilir. 1 kilobyte 1024 byte, 1 megabyte 1024×1024 byte ve 1 gigabayte 1024x1024x1024 byte’a karşılık gelir.

Modern bilgisayarlar, ikili ile hesaplamalar yapmak için transistör olarak bilinen şeyi kullanır. Bir transistörün işlevini şu biçimde düşünebilirsiniz. Bir bahçe hortumundan akan suyu düşünün. Bu suyun akışını kesmek için ortasına bir yere ayağınız ile basmanız yeterlidir. Şimdi bu akan su örneğini elektron yani elektrik akışı ile değiştirelim. Bu sistemde az evvel ayağın yaptığı işin bir kapı yapacaktır. Kapı açık ise 0, kapalı ise de 1 olarak adlandırılacaktır.
Üçlü Sayı Sistemi Kullansak Olmaz mı?
Transistör ilk icat edildiğinde, mantık kapıları ve toplayıcı gibi bilgisayar bileşenlerini yapmak için transistörlerin tek tek bağlanması gerekmekteydi. Ancak daha sonra milyarlarca ve milyarlarca transistörü eşzamanlı olarak tek bir silikon plakasına ya da çipine yerleştirmek mümkün olunca, bilgisayarlarda bir devrim gerçekleşti.
“Neden sadece 0 ve 1?” Bir rakam daha ekleyemez miyiz? Başka bir rakam eklemek, farklı akım düzeyleri arasında ayrım yapmamız gerektiği anlamına gelir. Bunun sonucunda sadece “kapalı” ve “açık” değil, aynı zamanda “biraz açık” gibi durumlar ortaya çıkabilir.
Bilgisayarlarımızda yer alan elektronik devreler 0 olarak yorumlanabilen “voltaj düşük” durumu ile 1 olarak yorumlanabilen “voltaj yüksek” durumu gibi iki farklı durumdan birinde bulunabilen basit sistemlerin birbirlerine bağlanmasıyla inşa edilir.

Birden fazla voltaj seviyesi kullanmak isterseniz, onlarla kolayca hesaplamalar yapmanın bir yoluna ihtiyacınız olacaktır. Aslında 1958 yılında Sovyet matematikçi Sergey Sobolev ve bilgisayar bilimci Nikolay Brusentsov, Setun adında üçlü sistemi kullanan bir bilgisayar geliştirdiler. Sonrasında bu bilgisayardan düzinelerce üretilmeye devam etti.
Peki üçlü sistem neden ikili sistemin yerini almadı? Bunun birincil nedeni gelenekti. Her ne kadar Sovyet bilim insanları üçlü sistemi kullanan bilgisayar üretse de dünyanın geri kalanı ikili hesaplama üzerine uzmanlaşmaya odaklanmıştı. Bu yüzden üçlü sistem, ikilinin yerini alamadı.
Kaynaklar ve ileri okumalar
- How Boolean Logic Works; Bağlantı: How Boolean Logic Works
- Why Computers Use Binary Numbers; Bağlantı: Why Computers Use Binary Numbers
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel