Geometride alan konusu işlenirken üçgen, dikdörtgen ve daire gibi temel şekillerin alanını öğretiriz. Ancak hesaplanması gereken alan daha karmaşık bir şekil olunca standart bir uygulama olarak şekli daha küçük temel parçalara bölerek bu alanların toplamından aranan alanı bulmaya çalışırız. Ancak kimi zamanlarda elimizdeki şeklin alanını parçalara bölerek hesaplamak da kolay olmaz. Bu noktada Pick teoremi yardıma yetişebilir.
Bu teorem 1899’da onu keşfeden Avusturyalı matematikçi Georg A. Pick’in (1859–1942) adını taşır. Ve kesinlikle parçalara bölerek yapılan alan hesaplarından çok daha kolay bir hesaplama biçimini bizlere gösterir. Bu yöntemi daha çok seveceğinizi düşünüyoruz.
Georg Alexander Pick (10 Ağustos 1859 – 26 Temmuz 1942), Holokost sırasında öldürülen Avusturyalı bir Yahudi matematikçiydi. Kendisi hayatını Theresienstadt toplama kampında kaybetti. Ölümünden önce kendisi de anlaşılan buluşandan oldukça mutlu olmuştu. Adı ile anılan teoremi keşfettiği zaman duygularını şu şekilde ifade etmişti.
“Uzun zamandır çok ilginç bir şeyi aydınlatmak için bekliyordum. En sonunda zarifliği ve basitliği ile dikkatimi çeken, geometri ile ilintili bir şey bulabildim. Hiç zaman kaybetmeyecek, doğrudan gerekli tanımlamaları ve teoremin kendisini derinlemesine araştıracağım.”
Pick Teoremi Nedir?
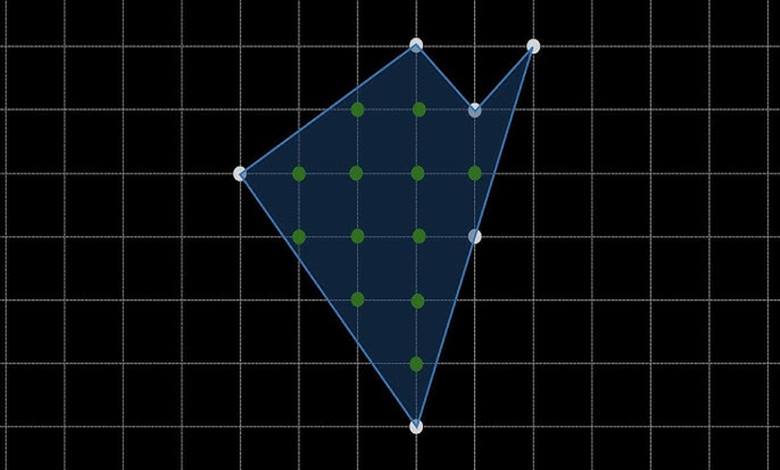
Bundan böyle alan bulmak için sadece nokta saymak yeterli olacaktır. Bir örnek üzerinden gidelim. Aşağıdaki mavi kenarlı çokgenin ( sağ tarafta gözüken) alanı kaç birim karedir?
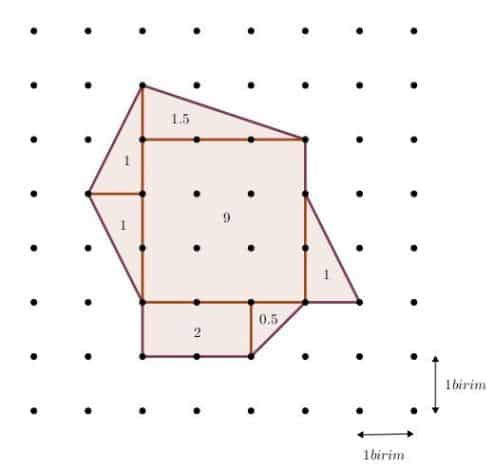
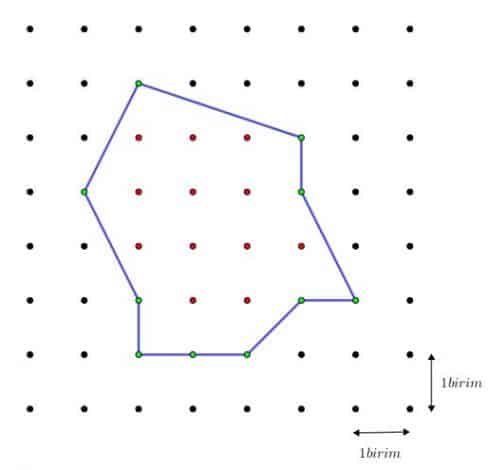
Böyle bir soruyla karşılaştığımızda ilk aklımıza gelen çözüm az evvelde dediğimiz gibi şekli alanını kolaylıkla hesaplayabileceğimiz çokgenlere ayırarak bunları tek tek toplamaktır. Geleneksel çözümle şekli içten parçalara ayırarak alanları toplamak suretiyle; Alan=1+1+2+1+9+1,5+0,5=16 birim kare olur.
Pick tarafından ortaya atılan yöntemle ise şu şekilde bulabiliriz. Çokgenin içindeki noktaların sayısı 12, çokgenin kenarları üzerindeki noktaların sayısı ise 10 dur. Alan= İç noktalar + Kenar üzerindeki noktaların yarısı -1 kadardır. Buna göre Alan= 12+5-1=16 birim kare olur.
Peki nasıl olur da herhangi bir çokgenin alanı sadece noktalar sayılarak bulunabilir? Teoremin işlemesi için çokgenin köşeleri noktalar üzerinde olacak ve çokgenin bir kenarı diğer kenarını kesmeyecek. Bu şartlar sağlandığı sürece bu teoremi kullanabiliriz. Bu kısıtlamaların teoremin güzelliğinden ve şaşırtıcılığından bir şey eksilteceğini düşünmüyorum. Umarım aynı fikirdeyizdir.
Pick Teoremi Neden Doğrudur?
Elimizde var olan çokgeni temel üçgenlere ayıralım ( Temel üçgen köşeleri noktalarda olan, iç bölgesinde ve kenarlarında başka noktalar barındırmayan üçgenlerdir.)
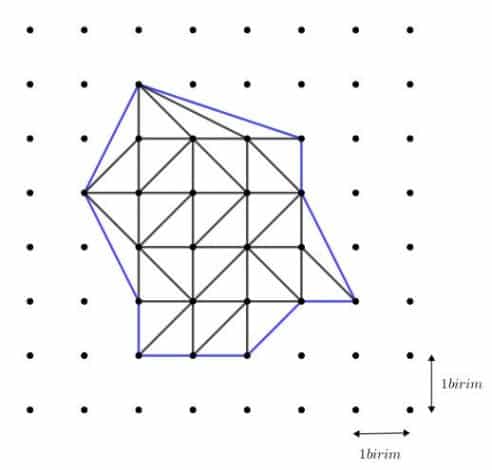
Çokgen N tane temel üçgenden oluşmuş olsun. Bu üçgenlerin iç açıları ölçüleri toplamı N.180 olacaktır. Şimdi bu açı toplamını bir de üçgenlerden faydalanarak yapalım. Yukarıdaki şekle dikkatlice bakarsak çokgenin içindeki noktaların (bunlara iç noktalar diyelim ve sayısını İ harfiyle gösterelim) etrafında oluşan her bir açı aynı zamanda içerideki üçgenlerin bir açısına denk gelmektedir. O halde her bir iç noktadan 360 derece gelecektir.
İ tane olduğundan toplam 360İ derece gelir. Çokgenin köşeleri ve kenarlar üzerindeki noktalara bakarsak köşe hariç her bir noktadan 180 derece gelecektir. Köşe noktaları da buna dahil ederek her birinden 180 derece gelecek şekilde hesaplayıp sonrasında fazlalık olanları çıkarmak suretiyle bu temel üçgenlerin iç açıları ölçüleri toplamına ulaşabiliriz. Köşe noktalarındaki fazlalık açıların toplamı bu çokgenin dış açıları ölçüleri toplamıdır. Bu da tüm çokgenler için sabit ve 360 derecedir.
Dolayısıyla kenar ve köşelerden toplam 180.K-360 derece gelir (K kenar ve köşe üzerindeki noktaların toplam sayısını göstersin). O halde N.180 = 360.İ + 180.K – 360 her tarafı 360’a bölersek; N/2= İ + K/2 – 1 formülü ortaya çıkar.
Sonuç Olarak;
Biraz daha toparlarsak bir temel üçgenin alanı 1/2 birim karedir. Tüm çokgen N tane temel üçgenden oluştuğuna göre çokgenin alanı N.1/2 birim kare olmuş olur. Buradan da çokgenin alanının; Alan: İ + K/2 – 1 olduğu sonucuna ulaşmış oluruz.
Yazımızın sonunda alan hesaplaması ile ilgili ilginç ve efektif bir başka teorem hakkında bilgi edinmek isterseniz bu yazımıza göz atmalısınız. Gauss Ayakkabı Bağcığı Yöntemi İle Alan Hesaplamasını Öğrenelim!
Kaynaklar ve ileri okumalar:
- Ball, K. (2017). Garip Eğriler, Tavşanları Saymak ve Diğer Matematiksel Keşifler. (Boğaç Karçıka)(1.baskı) Ankara: Tübitak Yayınları
- Sundström, Manya and Lars–Daniel Öhman. “Two beautiful proofs of Pick’s theorem.” (2011).
- Dubeau, François & Labbé, Sébastien. (2005). A general form of Pick’s theorem. International Journal of Pure and Applied Mathematics. 18.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel