Doğa düzensiz, karmaşık ve kaotiktir. Ancak daha yakından baktığınızda, en büyük sarmal gökadalardan en küçük salyangoz kabuğuna kadar her türlü farklı ölçekte desenler, diziler ve simetriler fark etmeye başlayabilirsiniz. Birçok yerde görülen popüler bir desen Fibonacci dizisi ve beraberinde Fibonacci spiralidir.

Eğer bir bitkinin yaprakların, bir anansın pullarını ya da bir çam kozalağını dikkatlice incelerseniz, farkında olmadan doğadaki matematiksel desenlerin muhteşem örneklerine tanık olursunuz. Çünkü verdiğimiz bu üç örnekte de Fibonacci spirali belirgin bir biçimde karşımıza çıkacaktır.
Fibonacci spirali gerçekten de bitkilerde son derece yaygındır ve Leonardo da Vinci’den Charles Darwin’e kadar bilim insanlarını tarih boyunca büyülemiştir. Aslına bakarsanız günümüzde Fibonacci spiralleri ile uyumlu olmayan çok az sayıda bitki vardır. Bitkilerde bu durum o kadar yaygındır ki, bunun evrimsel bir özellik olduğu düşünülmektedir.

Fibonacci spirali nedir?
Spiraller doğada sıklıkla karşımıza çıkar. Çoğu durumda, bu spiraller Fibonacci dizisiyle ilişkilidir. Fibonacci dizisi, her sayının kendisinden önceki iki sayının toplamı olduğu bir sayı dizisidir. 0 ve 1’den başlayarak, dizinin ilk 10 sayısı 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 biçimindedir.
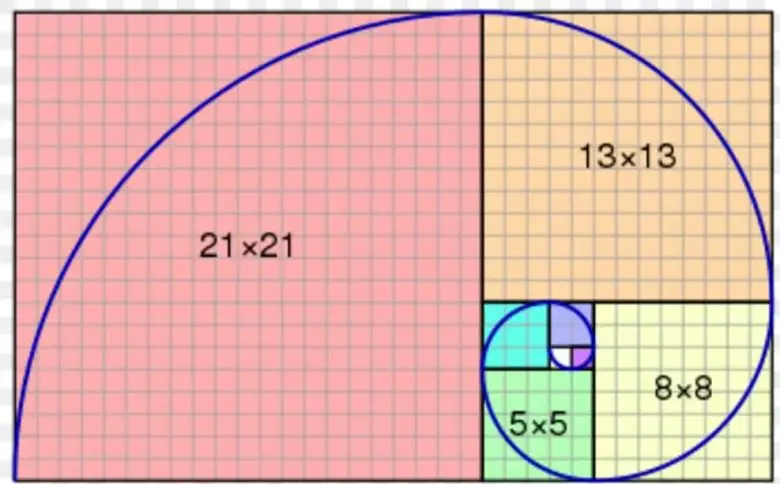
Fibonacci dizisindeki herhangi bir ardışık sayı çiftinin birbirine oranı kabaca 3/2 = 1.5, 5/3 = 1.6 biçimindedir. Seride ilerleyip daha büyük sayıları birbirine böldüğünüzde sonuç altın orana yaklaşır. Bu nedenle Fibonacci ve altın oran birbiriyle çok yakından bağlantılıdır.
Bazı bitkiler, her zaman Fibonacci dizisindeki sayılarla aynı sayıda büyüme noktasına sahip olacak şekilde dallanır. Buna bir örnek ananastır. Bir anansın pullarını dikkatlice incelerseniz 8, 13 ve 21 sayısına uyacak biçimde pulların dizilimine rastlarsınız.
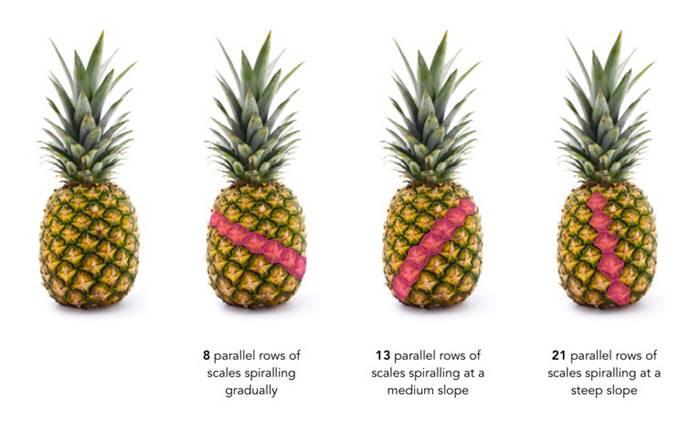
Benzer bir durum çam kozalakları için de geçerlidir. Bir çam kozalağı alıp incelerseniz ilk başta yalnızca tek yöndeki spiralleri görebilirsiniz. Ancak yakından baktığınızda hem saat yönünde hem de saat yönünün tersine spiraller görebilirsiniz. Hemen hemen her durumda spirallerin sayısı Fibonacci dizisindeki tam sayılar olacaktır.
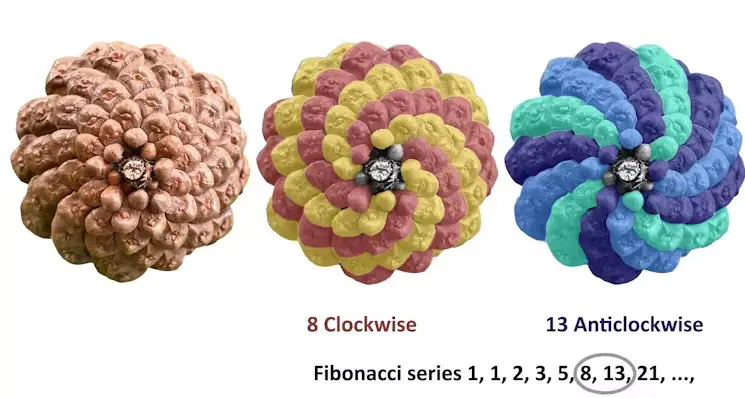
Bu istisnai bir durum değildir. 6.000 çam kozalağının incelendiği bir çalışmada, incelenen kozalakların %97’sinde Fibonacci spiralleri bulunmuştur. Üstelik Fibonacci spiralleri sadece çam kozalaklarında karşımıza çıkmaz. Ayçiçeğinde çiçeğin ortasından dışarıya doğru genişleyen spiraller bulacaksınız. Bu spirallerin toplam sayısı genellikle saat yönünde ve saat yönünün tersinde sırasıyla 34 ve 55 veya 55 ve 89 olacaktır.

Bir Bitkinin Büyüme Biçimi Fibonacci Spirali İle Neden ve Nasıl Bağlantılıdır?
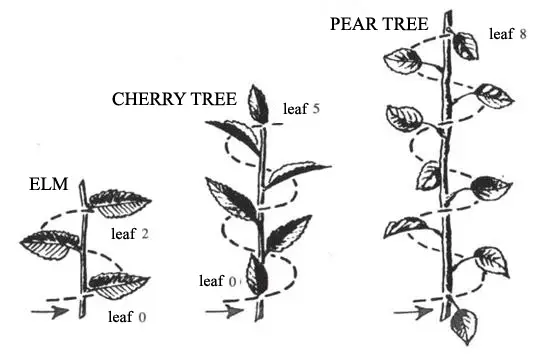
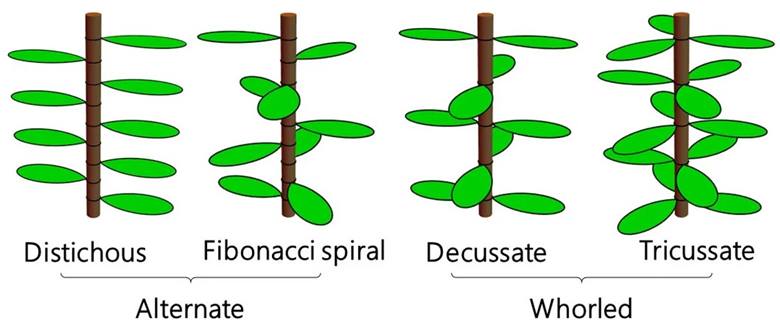
Fibonacci spirali yaprak ve çiçek gibi diğer bitki organlarında da yaygındırlar. Birçok bitkide, gövdeden filizlenen tek tek yapraklar olduğunu fark edeceksiniz. Bu yapraklar genellikle gövdeden farklı açılardan dışarı çıkar. Sonrasında da gövde yukarı doğru hareket ettikçe yapraklar bir spiral oluşturur. Her yaprağın bir öncekinden dönme açısı ise genellikle 137 ile 139 derece arasındadır.
Yapraklarda en sık ikili, üçlü, beşli dizilişler yer alır. Aslında tam da bu nedenle dört yapraklı yoncayı kolaylıkla bulamazsınız. Çünkü 4 sayısı yukarıda gördüğünüz sayı dizisinin bir elemanı değildir. 650’den fazla bitki türünden 12.000 spiral üzerinde yapılan bir araştırma, bu bitkilerin %90’ından fazlasında Fibonacci spirallerinin oluştuğunu göstermiştir.
Fibonacci spiralleri bitkilerde neden bu kadar yaygın?
Bu sorunun cevabını bilim insanları uzun süredir vermeye çalışıyorlar. Filotaksis bitkilerin yaprak düzenlemesini konu edinen bilim dalına verilen isimdir. Yaprak desenleri çalışmasının merkezinde yer alan varsayımlardan biri de farklı dizilimlerle, yaprakların kişisel alanlarını koruduğudur. Yani yeni büyüyen yapraklar mevcut yaprakların büyümesini engellemeyecek biçimde dizilmelidir.
Aslında her şey bitki bir tohumken başlar. Her yaprak ve taç yaprağı önce küçük bir tomurcuk gibi görünür. Tomurcuklar büyüdükçe kendisini bir öncekinden olabildiğince uzağa konumlandırmaya çalışır. Bunu muhtemelen büyüyebilmesi için gerekli alan ve ışığı elde etmek için yapar.
Bu noktada bir açı çok uygundur. Bu açı 360 derece bölü altın oran sonucunda elde edilen yaklaşık 222,5 derecedir. Saat yönünde 222,5 derece, saat yönünün tersine 137,5 derece ile aynı miktarda dönüşü temsil eder. Ayrıca, her tomurcuk bir öncekinden 137.5 derece döndürülmüş olarak ortaya çıkarsa, şemada gösterildiği gibi altıncı tomurcukta ilginç bir şey olduğu ortaya çıkıyor.
Dördüncü ve beşinci tomurcukların her ikisi de öncülleri ile aralarında en az 50 derece açıklık varken ortaya çıkan altıncı tomurcuk, ilk tomurcuktan yalnızca 32,5 derece uzaktadır. Bu, altıncı tomurcuğun güneş ışığına ve besinlere diğer tomurcuklardan biraz daha az erişimi olduğu anlamına gelir. Bu da büyüme ihtimalini azaltır.

Yukarıdaki görseldeki yaprakların her biri bir öncekinden tam olarak saat yönünde (222,5°) dönüş olacak şekilde numaralandırılmıştır. Gördüğünüz gibi 3. 5. ve 8. yapraklar farklı sıralarda yer almakta ve birbirini etkilememektedir.
Fibonacci Spiralleri İle Uyumlu Olmayan Bitkiler
Bir araştırma, bu bakış açısına meydan okudu. Çalışmada araştırmacılar soyu tükenmiş kulüp yosunu türü Asteroxylon mackiei’nin bitki fosillerini incelediler. Şaşırtıcı bir şekilde, bu türde gözlemlenen sarmalların aynı kurala uymadığını fark edilecekti.
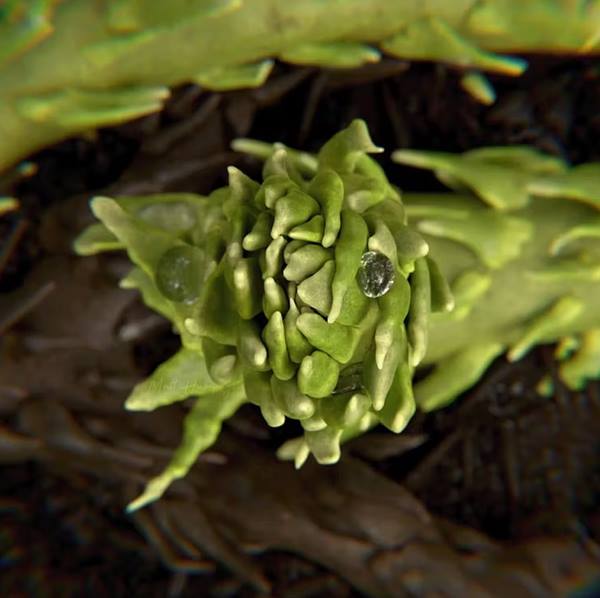
Bu bulgular kara bitkilerindeki Fibonacci spirallerine dair anlayışımızı değiştiriyor ve tüm yapraklı bitkilerin Fibonacci modelini takip eden yapraklar yetiştirmeye başladıkları ve bunun evrimsel bir avantaj sağladığı görüşünü bozuyor. Ayrıca bitkinin diğer bitki gruplarından farklı bir evrimsel geçmişi olduğunu gözler önüne seriyor.
Sonuç olarak
Son bulguların bu açıklama ile uyumlu olmaması doğadaki simetrinin bozulduğu anlamına elbette gelmiyor. Ancak anlaşılan doğada keşfedilecek daha çok fazla şey var ve biz mevcut bilgilerimizle her şeye henüz bir yanıt bulamıyoruz.
Kaynaklar ve ileri okumalar
- How a 400 million year old fossil changes our understanding of mathematical patterns in nature. Yayınlanma tarihi: 16 Temmuz 2023. Kaynak site: Conversation. Bağlantı: How a 400 million year old fossil changes our understanding of mathematical patterns in nature
- Smith, Richard & Guyomarc’H, Soazig & Mandel, Therese & Reinhardt, Didier & Kuhlemeier, Cris & Prusinkiewicz, Przemyslaw. (2006). A plausible model of phyllotaxis. Proceedings of the National Academy of Sciences of the United States of America. 103. 1301-6. 10.1073/pnas.0510457103.
- Alexander J Hetherington, Siobhán L Bridson. Anna Lee Jones, Hagen Hass, Hans Kerp, Liam Dolan (2021) An evidence-based 3D reconstruction of. Asteroxylon mackiei, the most complex plant preserved from the Rhynie chert eLife 10:e69447
- Leaves and sporangia developed in rare non-Fibonacci spirals in early leafy plants.Science380,1188-1192(2023).DOI:10.1126/science.adg4014
- Ridley, J.N.. (1982). Packing efficiency in sunflower heads. Mathematical Biosciences – MATH BIOSCI. 58. 129-139. 10.1016/0025-5564(82)90056-6.
- Are These 10 Natural Occurrences Examples of the Fibonacci Sequence? Yayınlanma tarihi: 4 Eylül 2024. Kaynak site: Discover Magazine. Bağlantı: Are These 10 Natural Occurrences Examples of the Fibonacci Sequence?
Matematiksel





