Bir şeyler içmek isterseniz, bunun için Klein şişesi kullanmanızı tavsiye edeceğimiz bir kap değildir. Uzaktan bakıldığında size bir şişe gibi görünebilir. Ancak bu şişenin herhangi bir hacmi yoktur. Yani aslında içine koyduğunuz herhangi bir sıvıyı tutamaz. Bu nedenle içine döktüğünüz her şey eninde sonunda tekrar dışarı çıkacaktır.

19. yüzyıl matematik için yaratıcı bir dönemdi. Bunun nedeni yeni bir araştırma alanı olan topolojinin ve beraberinde birçok yeni geometrik şeklin ortaya çıkmasıydı. Bu hareketliliğin başında August Möbius ve Johann Listing gibi matematikçiler yer alıyordu. 1858’de, ikisi de Listing’in ilk keşfettiği söylenen Möbius şeridi üzerine çalışmalar yapmaya başladı.
19. yüzyıl Alman matematikçisi August Möbius’un adını taşıyan bir Möbius şeridini kolayca yapmanız mümkündür. Ortaya çıkan şekil ise, karmaşık geometrik şekillerle ilgili anlayışımızı geliştiren bazı beklenmedik özelliklere sahiptir. Felix Klein ise iki Möbius şeridinden oluşan bir şekil olan Kleinsche Flasche’yi (Klein şişesi) tanımlar. Gelin şimdi bu iki şekli biraz daha yakından inceleyelim.
Möbius Şeridi Nasıl Yapılır?

Normalde bir yüzeyin iki tarafı olur: İçi dışı ya da önü arkası. Ancak Möbius şeridi oluşturulduktan sonra yalnızca bir yüzeye sahiptir. Aslında Möbius şeridi en basit tek taraflı yüzeydir ve bir kağıt şeritten yapılması kolaydır. İsterseniz hemen deneyebilirsiniz.
İnce uzun dikdörtgen biçiminde bir kağıt alın. Sonrasında bir yüzünü kırmızı noktalar diğer yüzünü ise yeşil noktalar ile boyayın. Şimdi şeridin iki ucunu alın ve bükün. Yani, kırmızı noktalı taraf yeşil noktalı tarafla birleşecek şekilde 180 derece çevirin. Ardından iki ucu birbirine yapıştırın. Bu bir Möbius şerididir. Bu şeridin yüzeyinde parmağınızı gezdirirseniz kırmızı ve yeşil noktaların her birine dokunabilirsiniz.
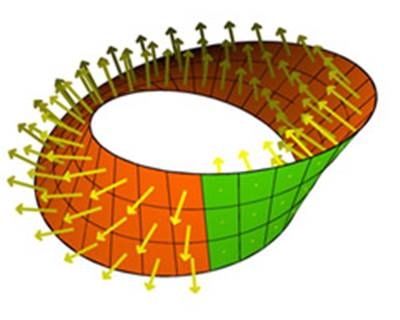
Elinizdeki şeridi yapıştırdığınız yerden ayırıp, bir kere daha kendi etrafında çevirirseniz aynı sonucu elde edemezsiniz. Ancak 3. defa çevirdiğinizde yine içi dışı aynı olan tek bir yüzeye sahip olursunuz. Genel olarak çift sayıda büküm her zaman iki taraflı bir yüzey üretecektir. Ancak tek taraflı bükümler ise size tek taraflı bir yüzey verecektir.
Basitliğine rağmen Möbius şeridi gerçek bir matematiksel keşifti. Topoloji, şekillerin sürekli eğilme ve esneme altında değişmeyen özelliklerini araştıran matematik disiplinidir. Yüzeylerin yönlendirilebilirliği hakkında akıl yürütme, topolojide yüzeyleri ve manifoldları anlamanın ve sınıflandırmanın anahtarlarından biridir. Möbius şeridi, üç boyutlu uzayda oluşturulabilen en basit, yönlendirilemeyen, iki boyutlu yüzeydir. ( Daha fazla detay okumak isterseniz: Yeni Başlayanlar İçin Topoloji: Nedir Ve Neden Önemlidir?)
Klein Şişesi Nedir?
Klein şişesi 1882’de Felix Klein tarafından keşfedildi. O zamandan beri de popüler matematiksel şekiller arasında varlığını koruyor. Klein şişesi de, Möbius şeridinin tuhaf özelliklerini taşıyan 3 boyutlu geometrik bir nesnedir.
Normal olarak bir şişenin bir iç bir de dış yüzeyi olması gerekir. Ancak bu Klein şişesi için geçerli değildir. Bu şişenin de tek bir yüzü vardır yani aslında iç yüzeyi ve dış yüzeyi birdir. Herhangi bir hacme sahip olmaması bu nedenledir. Ayrıca Klein şişesinin, kendi gövdesini delip “içine” giren, oradan da “dibine” açılan bir de boynu vardır.
Felix Klein 1880’de Leipzig’de profesör olduğunda bu şişeyi derslerde kullanılacak bir geometrik model olarak tasarlamıştı. Bu nedenle günlük yaşamda bir işleve sahip değildir. Ancak artistik bir biblo olmanın ötesinde önemli bir matematiksel değer taşır.

Klein şişesi yalnızca dört boyutlu uzayda bulunur, ancak bir Klein şişesinin modeli üç boyutlu olarak yapılabilir. Ancak bu model orijinal modelden farklıdır çünkü bir noktada şekil kendine temas etmek zorundadır. Ancak dört boyutlu uzayda durum bu biçimde değildir.
Klein Şişesi Nasıl Yapılır?
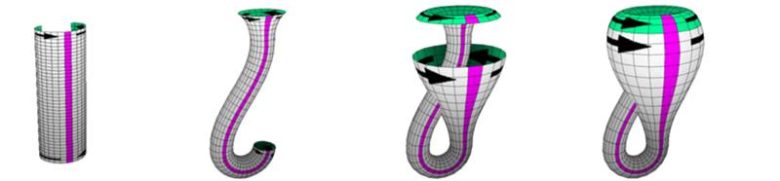
Möbius Şeridini yaparken, dikdörtgen biçimindeki şeridi uçlarından 180 derece ters olacak şekilde yapıyorduk. Klein Şişesi de bir silindiri aynı biçimde 180 derece ters olacak şekilde birleştirilerek elde edilir. Aşağıdaki kısa animasyonda standart bir Klein şişesinin nasıl yapıldığını görebilirsiniz.
Tekyüzlülük Ne Anlama Gelir?
Möbius şeridini veya Klein şişesini incelerken, yönlendirilebilirlik ve tek taraflılık önemlidir. Doğadaki çoğu yüzey iki taraflıdır. Örneğin, bir küre iki taraflıdır; bir torus, bir çubuk kraker ve daha genel olarak, katı bir hacmi çevreleyen tüm yüzeyler iki taraflıdır. Doğada genellikle tek taraflı yüzeyler görmeyiz. Bu nedenle Möbius tarafından bulunan tek taraflı yüzeyin soyut bir matematiksel yapı olduğunu söyleriz.
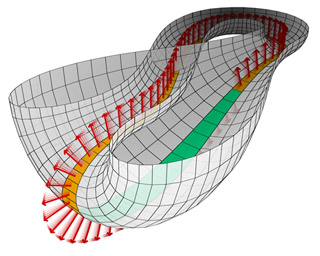
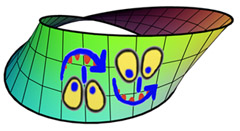
Yukarıdaki görselde Klein şişesindeki Möbius bandı boyunca dik oklar (normal vektörler) çizerek tek taraflılığını vurguluyoruz. Bu okları nereye çizerseniz çizin aynı yönü gösterecektir. Üzerine çizilen bir şekil, yüzey üzerindeki bir yol boyunca basitçe hareket ettirilerek ayna görüntüsüne dönüştürülemiyorsa, bir yüzeyin yönlendirilebilir olduğu söylenir.
Şimdi aşağıdaki görsele bakın. Sağda gördüğünüz gülen suratı Möbius şeridi etrafında hareket ettirseniz, sonunda şeklin ters dönmüş hali ile karşılaşırsınız. Bu da size şeklin yönlendirilemez olduğunu söyler. Tüm bunların elbette günlük hayatınızda size görünür bir faydası yoktur. Ancak çok boyutlu yüzeyler ile uğraşan bir matematikçi iseniz aynı şey söylenemez.
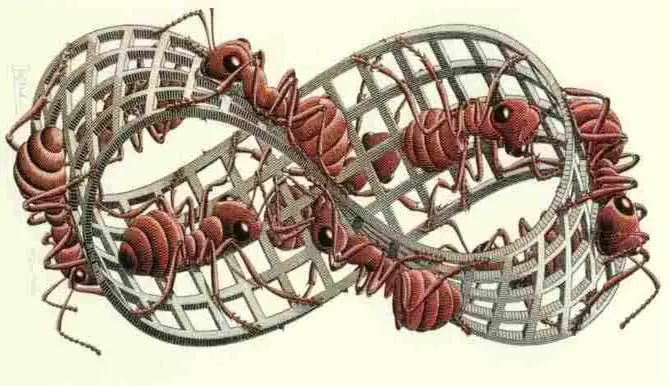
Klein şişesinin tuhaf özellikleri sayısız topoloji problemine olduğu kadar, sanat yapıtlarına, bulmacalara da ilham kaynağı olmuştur. Bu eser Alan Bennett’in İngiltere’nin Bedford Bilim Müzesi için yaptığı Klein şişesi dizisinden biridir. Eser birbirine geçmiş 3 Klein şişesinden oluşmaktadır.

Kaynaklar ve ileri okumalar:
- The Math Book: Big Ideas Simply Explained; Yayıncı: DK; ISBN-10 : 1465480242
- Imaging maths – Inside the Klein bottle; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










