Matematikte hakkında en çok tartışma yapılan sayı sıfır sayısıdır dersek muhtemelen yanılmış olmayız. Tartışmalardan birisi de sıfır sayısının doğal sayı olup olmadığı ile ilgilidir.

Bu tartışmanın nedeninin anlamak için öncelikle sıfır sayısının tarihi hakkında kısa bir bilgi edinmelisiniz. Aslında bunun sebebini anlamak da son derece kolaydır. Zamanda geriye gidip insanların sayılarla uğraşmaya başladıkları zamana bakarsak, sıfır ile ilgili bir kavramın olmadığını görürüz. Kimi uygarlık 23 ile 203’ü birbirinden ayırmak için iki sayı arasına bazı semboller ekleseler de, eklenen bu sembol daha çok yer tutucu görevi görmüştür.
Sonucunda matematiğin kökenleri sıfır sayısının yokluğunda atılmıştır. Sıfırın sayı olarak kullanımına da MS 7. yüzyılda Hintli bir matematikçi olan Brahmagupta (598–668) öncülük etmiştir. Ancak sıfır sayısı Avrupa’da ancak 300 sene sonra kabul görmeye başlamıştır. Kimi bölgelerde ise bu daha uzun bir zaman almıştır.

Örneğin 1299 yılında İtalya Floransa’da sıfır kullanımı yasaklanmıştı. 1500’lerde bile durum geçerliliğini koruyordu. Avrupalılar nihayet 1600’lerde İngiliz matematikçi John Wallis’in sayı doğrusuna sıfırı dahil etmesiyle sıfırı kabul ettiler.
Tüm bunları önceden bilmeniz aslında birazdan sizlere aktaracağımız kafa karışıklığının nedenini daha iyi anlamanızı sağlayacaktır. Bu karışıklık başta da dediğimiz gibi sıfır sayısının bir doğal sayı olup olmaması ile ilgilidir.

Sıfır Bir Doğal Sayı mıdır?
Herhangi bir ders kitabına göre doğal sayılar sıfırdan başlar. Aslına bakarsanız aynı durum yabancı dilde yazılmış ders kitaplarında da geçerlidir. Bu durumda sıfır bir doğal sayıdır biçiminde öğreniriz. Öte yandan bazı matematik kitaplarında veya akademik makalelerde sıfırın bir doğal sayı olarak ele alınmadığına da rastlamanız olasıdır. Peki hangisi haklı? Sıfır bir doğal sayı mı yoksa değil mi?
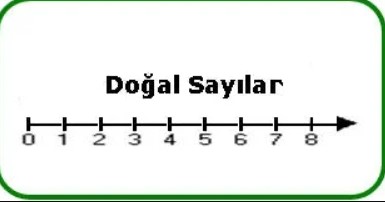
Aslına bakarsanız her iki kitap ve her iki fikri savunanda haklıdır. Bu temelinde hangi matematiksel yapıyı esas aldıkları ile ilgilidir. Sonucunda başta aktardığımız kısa tarihsel perspektiften de anladığınız gibi sıfır sayısı matematiğe 1, 2, 3 gibi sayılardan çok sonra dahil oldu. O dahil olduğunda da matematiğin temelleri halihazırda vardı.
Aslında sıfırın doğal sayı olup olmadığı doğal sayıların nasıl tanımlandığı ile ilgilidir. Doğal sayı, doğada yaygın olarak ve açıkça görülen bir sayıdır. Bu nedenle, negatif olmayan bir tam sayıdır ve N harfi ile gösterilir.
Doğal Sayılar Nasıl Tanımlanır?
Doğal sayının bir tanımı kümeler aracılığı ile yapılmaktadır. Bunun için kardinaliteye yani kümenin eleman sayısına bakılır. Sonuçta 1 elemanlı, 2 elemanlı, 3 elemanlı kümelerimiz olduğu gibi boş kümeyi de hesaba katarsak 0 elemanlı kümemiz de vardır. Bu tanımdan yola çıkarsak da N={ 0, 1, 2, 3…} kümesini elde ederiz. Yani bu durumda sıfır bir doğal sayı olur.
Ancak doğal sayıları tanımlamanın başka yolları da vardır. Aslına bakarsanız Küme teorisinde, doğal sayıları oluşturmak için birkaç yol önerilmiştir. Yukarıda çok basite indirgeyerek aktardığımız kardinaliteye bakarak doğal sayılar kümesini oluşturma yöntemi Gottlob Frege ve Bertrand Russell tarafından kullanılmıştır. Ancak sınırları bu yazının kapsamını zorlayacağı için dahil etmediğimiz başka doğal sayılar kümesini inşa etme yöntemi de vardır.
Bildiğimiz anlamda doğal sayılara yazılı olarak rastlayabileceğimiz ilk örnek, John Bonnycastle’ın 1782’de yazdığı bir matematik kitabıdır. Burada doğal sayılar kümesini 1 den başlayarak tanımlamıştır. Dedekind ve Peano da sayı teorilerine 0 ile değil 1 ile başlamışlardır. Sıfır sayısının doğal sayılar kümesine dahil edilmesi muhtemel modern matematik ve küme teorisinin gelişmesi ile olmuştur.
Sonucunda Dedekind’in küme teorisinde boş küme yoktu. Bu durumda elinizde boş küme yoksa sıfıra ihtiyaç duymuyor olmanız da olasıdır. Ancak Cantor’un küme teorisi versiyonu boş bir kümeye sahipti. Devamında gelen Hilbert, Frege, Russell ve Zermelo ve 20. yüzyılın geri kalan matematikçileri Cantor’un versiyonunu izledi. Bu durumda artık sıfır sayısı bir doğal sayı olmuştu.
Sonuç olarak;
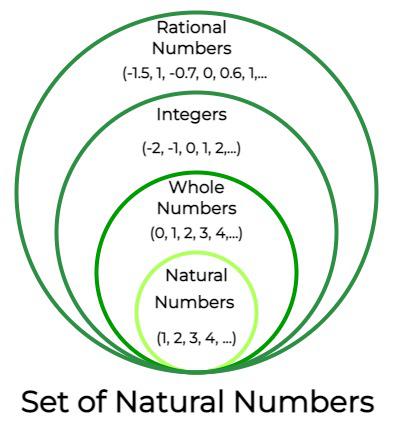
Sonucunda sıfır sayısının bir doğal sayı olup olmaması, doğal sayının tanımını nasıl yaptığınızla ilgilidir. Bu durumda her iki cevapta doğrudur. Hatırlamak da fayda var. Matematik, evrenin dilidir derken matematikçiler kuralların evren tarafından belirlendiğini anlatmaya çalışmazlar. Bu kuralları yine matematikçiler belirlemiştir. Önemli olan, tanımların doğru ve açık bir şekilde yapılması ve tutarlı bir matematiksel sistem inşa edilmesidir.
Ancak ülkemizde Milli Eğitim Bakanlığı doğal sayılar kümesine sıfırı dahil eder. Siz yine de bu bilgiyi doğru kabul edin. Öte yandan farklı biçimde tanımlayan bir yazıya ya da görsele denk gelirseniz de arka plandaki fikri öğrenmiş olun.
Sıfır sayısı ile ilgili bir başka tartışmayı da bu yazıdan okuyabilirsiniz. Sıfır Sayısı Çift mi, Tek mi Yoksa İkisi de Değil mi?
Kaynaklar ve ileri okumalar
- Is zero a natural number? Bağlantı: https://www.youtube.com/
- Natural number; Bağlantı: https://www.techtarget.com/
- Why is 0 a whole number but not a natural number? Bağlantı: https://www.quora.com
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel