Matematikçiler alışık olduklarımızdan farklı çalışan sayılara ihtiyaç duyar. Bunlardan biri de p-sel sayılardır.

Günümüzde sayılardan bahsettiğimiz zaman bir çok kişinin aklına doğal sayılar, tam sayılar gibi günlük hayatımızda kullanmaya alışık olduğumuz sayılar gelecektir. Ancak matematik konusunda çalışmalar yapan bir akademisyenseniz ve özellikle cebirsel geometri veya sayılar teorisi gibi konularda araştırmalar yapıyorsanız bu gibi temel sayı kümeleri size yeterli gelmeyecektir.
Bu kişiler alışık olduklarımızdan çok daha farklı biçimde çalışan sayılara da ihtiyaç duyarlar. Bunlardan birisi de p-sel sayılardır.
Öncelikle konunun popüler matematik yazıları yazan bir web sitesinde kısaca açıklanamayacak kadar karmaşık olduğu gerçeğini hatırlatarak işe başlayalım. Amacımız size ne olduğunu, ne ile ilgili olduğunu ve ne işe yaradığını anlatmak. Daha ileri düzey bir arayış içindeyseniz bu kaynağa göz atabilirsiniz.
P-sel Sayılar (P-adic numbers) Ne Anlama Gelir?
P-sel sayılar bir genellemedir. Buradan 3-sel sayılar, 5-sel sayılar biçiminde farklı sayı kümeleri elde edebilir ve onların özellikleri ile çalışabilirsiniz. “P” harfi de tahmin ettiğiniz gibi “Prime” yani asal sayılardan gelmektedir.

P-sel sayılar ile ilgili yapılan çalışmalar bugüne kadar matematikçilerin pek çok defa, matematiğin Nobel Ödülü kabul edilen Fields Madalyası almasını sağlamıştır. Aslında meşhur Fermat’ın son teoreminin 358 yıl sonra gelen çözümü de P-sel sayılar yardımı ile olmuştur.
Günümüzde topoloji düğümlerin veya geometrik şekillerin sınıflandırılması ile temelinde ilgilidir. Sayı teorisyenleri daha çok asal sayıların dağılımı gibi şeyleri araştırır. İkisi de oldukça kapsamlı matematik alanlarıdır. Ancak kendimizi biraz daha basit ilişkilerle sınırlandırırsak, başka bir modeli ele alabiliriz.
Dediğimiz gibi p-sel saylardaki P harfi prime yani asal sayı anlamına gelir. Ancak birazdan göreceğiniz bazı örneklerin asal olmadığını fark edeceksiniz. Aslında bunlar P-sel sayıların bir alt sınıfı olan 10-sal sayılardır. Buradaki 10 sayısı 10’luk sayma sisteminden gelmektedir. Şimdi p- sel sayıları anlayabilmek için öncelikle işe otomorfik sayılardan başlamamız gerekecektir.
Otomorfik Sayılar Nedir?
Genel olarak karesi alındığında kendisi ile biten sayılara “Otomorfik Sayılar” denir. Bunlardan bazılarını aşağıda görüyorsunuz. Görünen o ki, 0 ve 1 dışındaki tüm otomorfik sayılar ya 5 ya da 6 ile bitmektedir.
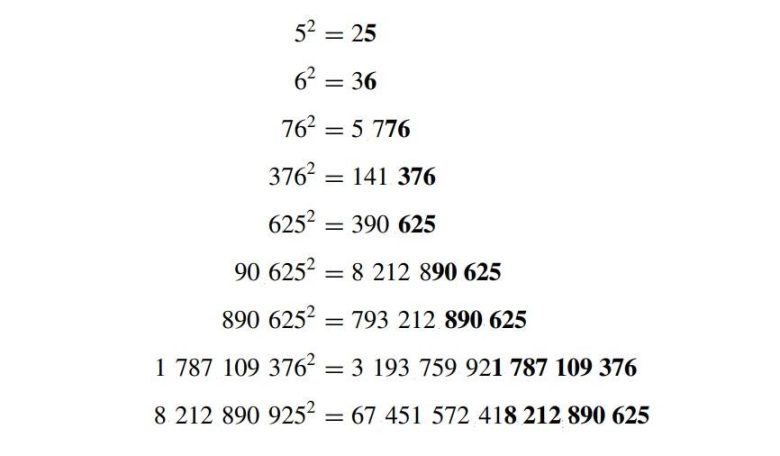
Ancak 5 sayısı özellikle heyecan vericidir. Çünkü sadece karesi değil ( 25), karesinin karesi de otomorfik bir sayıdır. Bu da doğal olarak otomorfik sayılar dizisinin süresiz olarak devam edip etmediği sorusunu gündeme getirir. Başka bir deyişle, 5’in tekrarlanan karesi her zaman otomorfik bir sayı mı üretir?
Aslına bakarsanız üçüncü kareden sonra model çöker. Çünkü 390,6252 = 152.587.890.625 biçimindedir. Dolayısıyla 390.625 otomorfik olamaz çünkü sayı tamamen karesinde yer almamaktadır. Fakat dikkatli bakarsanız son beş rakamın yani 90.625’in sonuçta yer aldığını görebilirsiniz. Ve bu sayının karesini alırsanız 8.212.890.625 sonucunu elde ederseniz.
Dolayısıyla 90.625 otomorfik bir sayıdır. Bu, devam edip 8.212.890.625‘in karesini hesaplayabileceğiniz anlamına gelir. Karesi 67.451.572.418.212.890.625 biçimindedir ve bu da 8.212.890.625’in de otomorfik sayı olduğu anlamına gelir.
Sürece bu biçimde devam edebilirsiniz. Sayının karesini alın ve sonuç otomorfik olmazsa , tekrarlanan son rakamlarla hesaplamalara devam edin. Bu, aşağıdaki gibi bir sonucu size verecektir. Gördüğünüz gibi bu, giderek daha büyük bir otomorfik sayıyla sonuçlanır.

Aslına bakarsanız bu sürece istediğiniz kadar devam ettirebilirsiniz. Sonuçta elde edeceğiniz sonsuz büyüklükteki sayıyı yazamasanız bile son basamaklarının …918,212,890,625 biçiminde olduğunu biliyor olacaksınız. Peki tüm bu sayılar ne anlama gelir?
P-sel Sayılar İle Ne Yapabiliriz?
19. yüzyılın sonlarında matematikçi Kurt Hensel, p -sel sayılar olarak adlandırılan kavramı geliştirdi. Sonsuz büyüklüklerdeki sayıları genelde π = 3,14159… gibi, virgülden sonra devam eden basamaklarla görmeye alışkınız. Bu sayılar virgülden önce sonsuz sayıda basamağa sahip olan sayılardı.
Oysa ki virgülden önce sonsuz sayıda basamağa sahip olan sayılar da vardı ve bu sayılarla da normal sayılarla yaptığımızı gibi işlemler yapmamız mümkündü. Kurt Hensel p-sel sayıları sonsuz bir seri olarak düşündü. Mesela …890625 = 5 x 100 + 2 x 101 + 6 x 102 + 0 x 103 + 9 x 104 + 8 x 105 + …. biçiminde ifade edilebilir.
Bu şekilde ifade edersek, bu garip sayılar ile nasıl işlem yapılabileceğini kabaca anlamış olursunuz. Bu durumda örneğin 3-sel sayılar x0 x 30 + x1 x 31 + x2 x 32 + x3 x 33 + x4 x 34 + x5 x 35 + .. biçiminde ifade edilecekti. . ( Burada xi nin katsayıları 0, 1 veya 2 olmalıdır. )
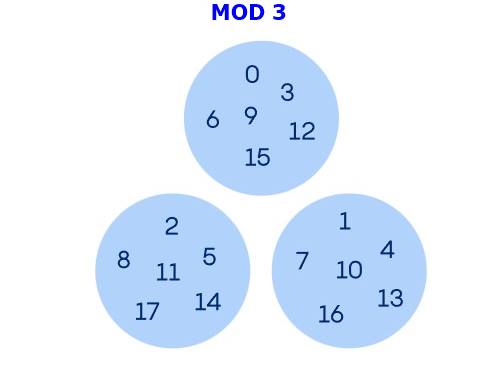
P-sel sayılar modüler aritmetikle de ilgilidir. Nasıl bir ilişkisini anlamak için yukarıdaki sayılara göz atalım. Her bir kutucuğun içinde 3 ile bölündüğünde aynı kalanı veren sayıları görüyorsunuz. Benzer bir biçimde mod 9 veya mod 27 içinde kalanlar sınıflarını yazmamız mümkündür. Bu durumda aşağıdaki gibi bir sonuç elde ederiz.
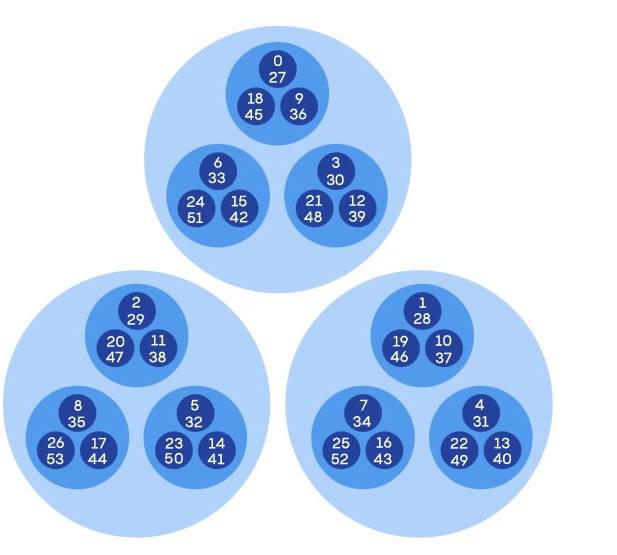
Bir p-sel sayının boyutu asal çarpanlarına ayırma ile belirlenir. İçinde daha fazla “p” olan sayılar daha küçüktür. Örneğin 3- sel sayılara göre 486 “küçük”tür çünkü asal çarpanlarına ayırırsanız içinde birçok 3 vardır (486 = 2 x 3 x 3 x 3 x 3 x 3). Bu sayılar ile işlem yapmanın da olası olduğundan bahsetmiştik. Ancak elbette bu işlem sonuçları oldukça ilginç olacaktır.
Örneğin 486 + 486 = 972 yapar. Reel sayılarda 972, 486’dan büyüktür. Ancak 3-sel sayılarda 972, 486 ile aynı büyüklüktedir. Çünkü hem 972 hem de 486 asal çarpanlarına ayrıldığında aynı sayıda 3 içermektedir.
Sonuç olarak
P-sel sayılar ilk bakışta son derece karmaşık görünse de yaygın olarak kullanılmaktadır. Aslında sayı teorisyenleri çalışmalarının çoğunda bu tuhaf değerleri kullanır. Örneğin matematikçiler 3x3 + 4y3 + 5z3 = 0 gibi polinom denklemlerinin ne zaman rasyonel çözüme sahip olduğunu bilmek isterler. Bu genellikle zor bir sorudur. Ancak p-sel sayılar yardımı ile çözümler bulmak nispeten kolaydır.
Matematikçilerin bu soruyu yanıtlamak için kullandıkları araçlardan biri 1920’lere dayanan Hasse ilkesidir. Bu ilke, bir polinomun gerçel sayılarda ve tüm p-sel sayılarda bir çözümü varsa, bu polinomun rasyonel sayılarda da bir çözümü olduğunu öne sürer.
Fermat’ın ünlü son teoremi 358 yıl boyunca çözülmeye bekleyen en ünlü problemlerden biridir. Aslında bu problemin çözülebilmesi için yeni sayı sistemlerinin geliştirilmesi gerekmiştir. Bu sayı sistemi ise p- sel sayılardır. Konu başta da dediğimiz gibi bir web sitesinde açıklanamayacak kadar karmaşıktır. Ancak aşağıdaki video da size bu konuda fikir verecektir.
Kaynakla ve ileri okumalar
- Simple Math Creates Infinite and Bizarre Automorphic Numbers. Yayınlanma tarihi: 11 Ocak 2024. Kaynak site: Scientific American. Bağlantı: Simple Math Creates Infinite and Bizarre Automorphic Numbers
- An Infinite Universe of Number Systems. Yayınlanma tarihi: 19 Ekim 2020. Bağlantı: An Infinite Universe of Number Systems
- Fried, Michael. (1980). A Note on Automorphism Groups of Algebraic Number Fields. Proceedings of The American Mathematical Society – PROC AMER MATH SOC. 80. 386-386. 10.1090/S0002-9939-1980-0580989-8.
- Mathematicians Use Numbers Differently From The Rest of Us. Kaynak site: Youtube.
Matematiksel