Andrew Wiles ve Fermat’ın Son Teoreminin İspatlanma Hikayesi

Bu yazı, dünyanın en büyük matematik problemini kendine takıntı haline getirmiş bir adamın hikâyesidir. Bahsettiğimiz kişi Profesör Andrew Wiles, uğraştığı son problem ve yazının konusu da Fermat’ın Son Teoremidir.

Wiles’ın tarihte bir yer edinmesine neden olan sorunun öyküsü, 1637’de Pierre de Fermat’ın şaşırtıcı derecede basit bir varsayımda bulunmasıyla başlar. Fermat, bir kitabın sayfa kenarına bir teorem önerisi not etmiş ve ardından da ispatı yazacak yeri olmadığını ama ispatı yaptığını söylemişti. Fermat’ın iddiası aşağıda gördüğünüz gibiydi.

Matematikçilerin kalbini çalan şey bu iddia ve söz konusu problemin basitliği oldu. Kuşaklar boyunca matematikçiler, ispatı keşfetmek için boşuna uğraştı; bütün ömrünü teoremle boğuşarak geçiren ve eli boş ölüp giden birçok matematikçi de oldu.

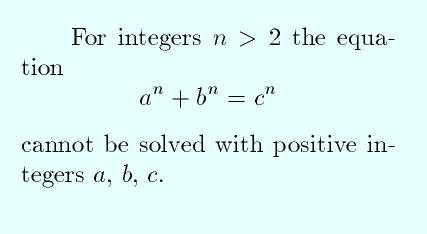
Teorem, ileri sürülen binlerce yanlış kanıtla birlikte, kanıtlanmasının inanılmaz derecede zor, hatta imkansız olduğu yönünde kısa sürede ün kazandı. Hatta teorem Guinness Dünya Rekorları’na “en zor matematik problemi “olarak da girdi.

Andrew Wiles, halk kütüphanesi raflarından tesadüfen çekip çıkardığı bir kitaptan Fermat’nın Son Teoremi hakkında bir şeyler öğrendiğinde on yaşındaydı. Ancak oldukça basit göründüğü için hemen çözülecekmiş gibi gözüken bu problemi çözmenin Ay’a roket fırlatmaya çalışmaktan daha kolay olmadığını kısa sürede anlayacaktı.

Wiles ilerleyen süreçte, 1974’te Oxford Üniversitesi’nden lisans derecesi ve 1980’de Cambridge’den doktora derecesi aldı. Wiles, bir yetişkin olarak yedi yıl boyunca problem üzerinde gizlice çalıştı. Başarı olasılığı konusunda öyle büyük bir tereddüt yaşıyordu ki teorem üzerinde çalıştığını kız arkadaşına bile, evlenmelerine kadar söylemedi. O sıralarda aynı zamanda eliptik eğrilerin aritmetiği üzerinde çalışmalar yapıyordu. Ancak bu eğrilerin, Fermat’ın son teoremi ile ilintili olduğundan haberi yoktur.

Eliptik eğriler ve modüler formlar arasındaki ilişki nedir?

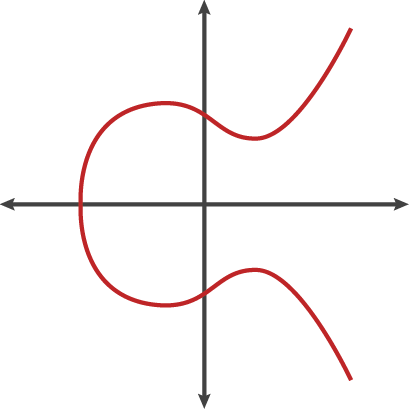
Wiles problem üzerinde uğraşırken, daha önce hiç bir araya gelmemiş matematiksel teknikleri harmanladı. Bunlar eliptik eğriler ile modüler formlardı. Eliptik eğriler ne elips ne de eğridir. Eliptik bir eğrinin denklemi y² = x³ + ax + b biçiminde olur ve bunlar kübik denklemlerin çözüm uzaylarıdır.

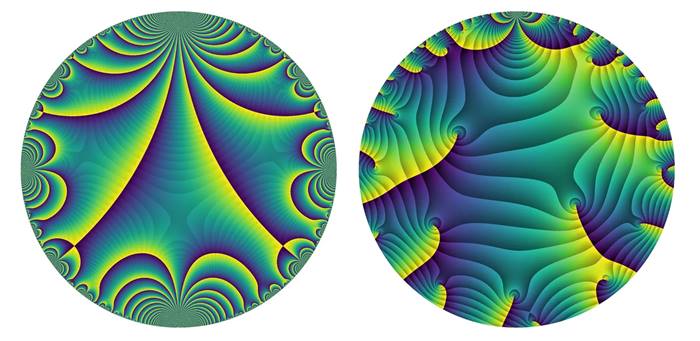
Modüler form ise, belirli karmaşık sayıları alan ve başka bir karmaşık sayı veren bir tür fonksiyondur. Modüler formlar barındırdıkları simetriler ile matematikçilerin ilgisini çeker. Her türlü problemde ortaya çıkarlar ve Sicim teorisi ve kuantum fiziğindeki modelleri incelemek için bile kullanılırlar. Bunlar, sayı teorisindeki en büyük açık sorulardan birini çözen Andrew Wiles’ın kanıtında da önemli bir bileşendi.

1950’lerden beri Taniyama-Shimura varsayımı, her eliptik eğrinin bir modüler formla bir biçimde eşleştirilebileceğini belirtir. Tuhaf modüler formlar, eliptik eğrilerin dünyasıyla bağdaşmıyor gibi gözükürr. Ancak Taniyama ve Shimura’nın öne sürdüğü hipotez bunları bağlar.

1985 yılında Alman matematikçi Gerhard Frey Fermat’ın son teoreminin eliptik eğrilerle bağlantılı olabileceğini düşündü. Daha sonra Ken Ribet, Fermat’ın son teoremi ile Taniyama-Shimura varsayımı arasında bir bağlantı kurdu. Fermat’ın son teoremi yanlış olsaydı Taniyama-Shimura-Weil varsayımı da yanlış olurdu. Tam tersi, doğru olursa da Fermat haklı olmalıydı.

Fermat’ın son teoremini kanıtlamak için Wiles, Taniyama-Shimura varsayımını kanıtlamak zorundaydı. Ancak bu durum birçok matematikçinin imkansız olduğunu düşündüğü bir görevdi. Wiles, bunu kanıtlamanın tek yolunun Princeton’daki evinde gizlice çalışmak olduğuna karar verdi. Etrafının ilgisini çekip aklını karıştırmamak için bu gizlilik ve yalnızlık gerekliydi.

Andrew Wiles Fermat’ın Son Teoreminin Kanıtı İle Abel Ödülü Aldı

1993 yılına gelindiğinde, modülerlik varsayımının özel bir durumunun kanıtını elde etmeye çok yaklaşmıştı. Fermat’ın son teoremini kanıtlamak için ihtiyacı olan tek şey buydu. Çalışmasını Haziran 1993’te Isaac Newton Enstitüsü’nde bir dizi konferansta sundu.

Haber, saatler içinde dünyanın dört bir köşesinde manşetlere taşındı. Sonucunda bu tarihsel bir andı. İnsanlığın en zorlu entelektüel problemlerinden biri üzerinde harcadığı onca çabanın ardından, Andrew Wiles bir anda uluslararası bir şöhret haline gelmişti.

Ne yazık ki Wiles için bu hikayenin sonu değildi. Wiles bir hata yapmıştı. Çalışmasını değerlendiren matematikçiler, izlediği mantıkta bir boşluk yakalamıştı. Yaptığı cesurca duyurunun üzerinden altı ay geçmişti ki ispat, geçerliliğini yitirmişti. Wiles ve eski öğrencisi Richard Taylor sorunu çözmek için bir yıl daha çalıştı. Bir yıllık düzeltme çabasının ardından tam vazgeçmeye hazırken hatasını buldu.

Sonuç olarak

Yaptığı hatalarla yılmayan matematikçi, bitiş çizgisini geçmiş ve böylece hayatının kumarından kazançlı çıkmıştı. Andrew Wiles’ın ispatı Annals of Mathematics dergisinde 1995 yılında yayımlandı. Bu başarısının ardında yatan şey çocukluk hayalleri ve bitmek bilmeyen tutkusuydu.

Fermat’ın son teoreminin ve çözümünün etkileri matematik dünyasında yankılanmaya devam ediyor. 2001 yılında aralarında Taylor’un da bulunduğu bir grup araştırmacı, Wiles’ın çalışmalarından ilham alan bir dizi makalede modülerlik varsayımının tam kanıtını sundu. Eliptik eğriler ve modüler formlar arasındaki bu köprü, Fermat’ın son teoreminin çok ötesine geçti. Bu sayı teorisinde yeni bir çağın başlangıcı anlamına da geliyordu.

Peki son olarak Fermat’ın iddia ettiği gibi son teoreminin ispatı gerçekten var mıydı? Günümüzde matematikçiler sorunun cevabını bildikleri için bunun pek de olası olmadığını düşünüyorlar. Fermat muhteşem olmasına rağmen bazen yanılıyordu. Belki de kendisini bir kanıt bulduğuna inandırmıştı. Ancak bu kanıtının modern incelemelere dayanması olası olamazdı.

Kaynaklar ve ileri okumalar:

• Castelvecchi, D. Fermat’s last theorem earns Andrew Wiles the Abel Prize. Nature 531, 287 (2016). https://doi.org/10.1038/nature.2016.19552
• Proving Fermat’s last theorem. 2 mathematicians explain how building bridges within the discipline helped solve a centuries-old mystery. Yayınlanma tarihi: Kaynak site: Conversation. Bağlantı: Proving Fermat’s last theorem. 2 mathematicians explain how building bridges within the discipline helped solve a centuries-old mystery
• Fermat’s last theorem and Andrew Wiles; yayınlanma tarihi: 1 Haziran 2008. Bağlantı: Fermat’s last theorem and Andrew Wiles/

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel