Günlük hayatımızı sürdürmek için logaritmaya pek de ihtiyaç duyulmuyor gibi gözüküyor. Peki durum gerçekten bu mu? Gelin logaritma nedir, ne değildir bir kere daha anımsayalım.

Çok da uzun olmayan bir zaman önce, karmaşık hesaplamaları yapmak için, hesap makinelerinde log() düğmesi yoktu ve matematikçiler işlemleri elle yapılmak zorundaydı. 16. ve 17. yüzyılların bilimsel devriminde, güvenilir bir hesaplama aracının olmaması ilerlemenin önüne bir engeldi.
Günümüzde bize sadece derslerde ezberlenmesi gereken bir dizi sıkıcı kurallar gibi gelse de logaritma insanlığın teknoloji ile tanışmadığı dönemlerde hesaplama yapabilmenin tek yoluydu. Ancak logaritma ilk icat edildiği zamanlarda günümüzdekinden çok daha farklı biçimde kullanılıyordu.

Logaritma Nedir?
Günümüzde logaritmayı üstel fonksiyonun tersi olarak tanımlasak da, başlangıçta logaritmalar bir hesap tablosu gibi görülüyordu. Yani logaritma bir nevi ilkel hesap makinesi idi. Temel olarak logaritmalar çarpmayı toplamaya, bölmeyi de çıkarmaya, n’inci dereceden kök bulma işlemini 1/n ile çarpmaya çevirmeye yarıyordu.
Hesap makinesi öncesi dönemde bu çok değerliydi. Astronomik hesaplamalar çok büyük sayıların çarpılmasını ve bölünmesini gerektiriyordu, bu da hesap makinesi olmadan yapılması oldukça zor bir şeydi. Üstelik günümüzde e tabanında logaritma ( ln) olarak tanımladığımız doğal logaritmalar, e sayısı keşfedilmeden on yıllar önce kullanılmaya başlanmıştı.
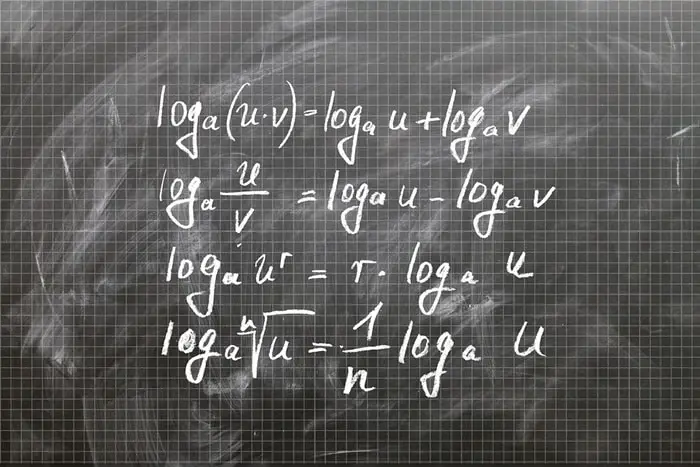
Şimdi gelin logaritma ile bir işlem yapalım. Örneğin 89 ile 62’yi çarpalım. 89’un logaritması 1.949’dur. 62’nin logaritması ise 1.792’dir. O halde logaritmalar toplamı 1.949 + 1.792 = 3.741 yapar. Logaritması 3.741 olan sayı ise 5518’dir. Bu da aynı şekilde logaritma tablolarından faydalanarak bulunur. O halde, 89 x 62 = 5518 ‘dir.
Logaritmayı Kim Buldu?
İnsanlar Arşimet’ten beri, 2 ile başlayıp ardışık iki katına çıkarılarak elde edilen dizi (2, 4, 8, 16, 32, 64, 128,… .) ile 1, 2, 3, 4, 5, 6, 7, … biçimindeki sayma sayıları arasında bir ilişki olduğunun farkındaydı. Günümüzde İlk diziye geometrik dizi diyoruz çünkü ardışık sayılar aynı orana sahiptir. İkinciye ise aritmetik dizi deriz, çünkü ardışık sayılar aynı farka sahiptir.

İnsanlar, geometrik dizideki iki sayıyı çarpmanın (veya bölmenin) aritmetik dizideki karşılık gelen sayıları toplamaya (veya çıkarmaya) karşılık geldiğini de zaman içinde fark ettiler. (Bizim için bunlar sadece üs alma yasalarıdır.) Bu, geometrik dizideki zor işlemleri aritmetik dizideki daha kolay işlemlerle değiştirebileceğiniz anlamına da geliyor.
Sonunda İskoçyalı matematikçi John Napier bu işe kafa yormaya başladı. Napier, geometrik dizideki sayılarla, karşılık gelen bir aritmetik dizideki sayıları ilişkilendiren bir tablo oluşturmak istedi. Bunun için basit bir mantık yürüttü. Aşağıdaki tabloda soldaki sütun, ikinin katlarından oluşan geometrik diziyi, ikinci sütun ise ortak farkı 1 olan aritmetik diziyi göstermektedir.
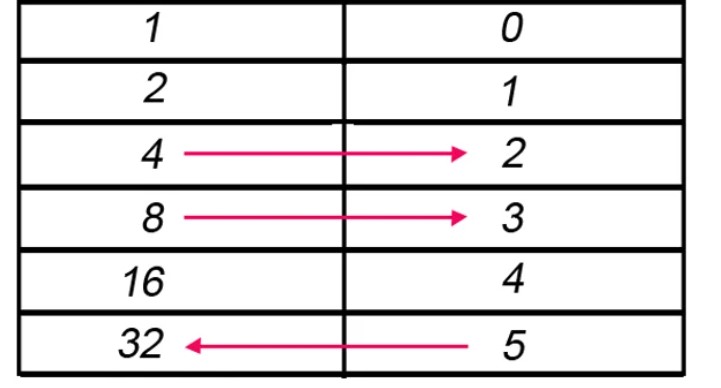
4 ve 8’i çarpmak için, ikinci sütundaki karşılık gelen terimleri toplayabiliriz. Bu bize 2 + 3 = 5’i verir ve 5’e karşılık gelen terimi kontrol ettiğimizde, çarpımının 32 olduğunu görebiliriz. Bu şekilde çarpmayı toplamaya çevirerek basitleştirdik. Benzer şekilde, bölmeyi de çıkarmaya çevirebiliriz.
Doğal Logaritma Nedir?
Napier aritmetik diziyi gösteren ikinci sütunda karşılık gelen sayılara yapay sayılar adını verdi. Ancak daha sonra bunu iki Yunanca kelimeden türettiği ( Logos+Arithmos – Orantılı sayı) bir kelime ile yani logaritma olarak isimlendirdi.
Yukarıda verdiğimiz örnek, algılanması kolay sayılardan oluşsa da fazla da pratik değildir. Çünkü geometrik dizimizi ikinin katlarını içerecek biçimde sınırlarsak, sayıların arasında giderek daha fazla boşluk olacaktır. Örneğin 2 ile 4 arasında 3 sayısı yok. Bu durumda 3 sayısının logaritmasını bulmamız mümkün değildir. Boşlukları doldurmanın bir yolu, bir sayısına çok yakın bir taban seçmektir.
Napier bu konu üzerine çok kafa yordu. Sonunda 0,9999999 gibi bir sayı seçti ve ilk sayıyı 1 yerine 10 milyon olarak aldı. Hesaplamalarını yaparken de kendi zamanında mevcut olan sinüs tablolarını kullandı. Ancak yine de 90 sayfalık bir logaritma listesi derlemesi 20 yılını alacaktı. Çalışmalarının sonuçlarını 1614 yılında yayımladı.

Kitap bilim camiası tarafından coşku ile karşılandı ve kısa sürede logaritmaların farklı versiyonları ortaya çıkmaya başladı. 1618 yılında, Napier’in kitabının çevirilerinden birinde, Napier’in öğrencilerinden biri olana William Oughtred tarafından yazılmış olan kitapta var olan tablolarda ilginç bir ilişki göze çarpıyordu.
Bu tabloda var olan sayılar günümüzde kullandığımız doğal logaritmanın karşılığına denk gelen sayılara yakından benziyordu. 1622 yılında John Spedell kendi logaritma tablolarını yayınladı. Benzer biçimde bu tablodaki sayılar da doğal logaritma ile uyumlu idi.
Her iki matematikçi de logaritma ve üstel sayılar arasındaki herhangi bir bağlantıyı bilmeden doğal logaritmaya benzeyen sonuçlara ulaşmışlardı. Bunu yapmak için de geometrik artışı 0’dan küçük değil, 1,000001 gibi sıfırdan çok az büyük bir sayı seçmişlerdi. Aynı zamanda aritmetik artışı da 0,000001 gibi çok küçük bir ortak farkla sınırlamışlardı.
Matematikçiler farkında olmasalar da doğal logaritmayı, daha e sayısının ne olduğunu anlamadan hesaplamışlardı.
Logaritmaya Ne İşe Yarar?
1960’lardan itibaren hesap makinesi ve bilgisayarın hayatımıza girmesiyle logaritmayı elle hesaplamaya ihtiyaç azalsa da birçok fiziksel ve biyolojik sürecin davranışı logaritmik olduğu için logaritma halen matematiğin içinde önemini korumaktadır.

Günümüzde logaritma tabloları artık kullanılmasa da kendileri bilgisayarlarımızda var olmaya devam ediyor. Bilgisayarda sayıları çarpmak istediğimiz zamanlarda arka planda bir program çalışır. Bu programın sonuç verme süresi karmaşıklık ve hesaplama miktarı ile artar.
Saniyede milyonlarca sayının çarpılması gereken ve hızın kritik olduğu bir uygulamada bu bir sorun haline gelir. Bu nedenle bilgisayar belleğine bir program çalıştırmak yerine yalnızca değerleri araması gereken ve performansı artıran logaritma tabloları eklenir.
Logaritmaların bilimde birçok kullanımı vardır. Aslına bakarsanız üstel büyümenin olduğu hemen her yerde logaritma bir biçimde işe karışacaktır. Bu nedenle günümüzde tabloları kullanmaya gerek kalmasa da arka plandaki fikri bilmek hala gereklidir.
Kaynaklar ve ileri okumalar:
- What Are Logarithms? Yayınlanma tarihi: 22 Mayıs 2015. Kaynak site: Live Science.. Bağlantı: What Are Logarithms?
- The making of the logarithm; yayınlanma tarihi: 14 mart 2014; Kaynak site: Plus math. Bağlantı: The making of the logarithm
- Roegel, Denis. (2010). Napier’s ideal construction of the logarithms.
- Evans, John Ellis. “Why Logarithms to the Base e Can Justly Be Called Natural Logarithms.” (1939).
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel









Teşekkürler.