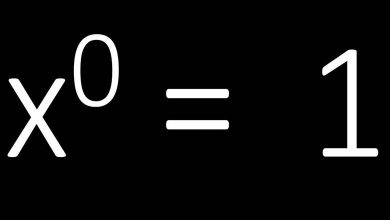“Sonsuzun karekökü nedir?” sorusu ilk bakışta saçma görünebilir. Ancak sürreel (gerçeküstü) sayılar perspektifinden bakıldığında, bu sorunun bir cevabı vardır.

1970’lerin başında, ünlü matematikçi Donald Knuth, eşiyle birlikte Norveç’te tatildeydi. Keyifli bir zaman geçirirken, bir gece aniden tarif edilemez bir yazma isteğiyle uyandı. Bu durumu eşiyle paylaştıktan sonra, Oslo’da kendisine bir otel odası ayarladı ve burada ünlü kitabı “Surreal Numbers: How Two Ex-Students Turned On to Pure Mathematics and Found Total Happiness” adlı eserini yazdı.
Knuth, sürreel sayıların mucidi değildi, ancak bu kavram üzerine kapsamlı bir çalışma yayımlayan ve terimi popüler hale getiren kişi oldu. Günümüzde, bu kitabı sürreel sayılar üzerine yazılmış temel eserlerden biri olarak kabul edilir.

Gerçeküstü Sayılar Nedir?
COVID-19 nedeniyle hayatını kaybeden efsanevi matematikçi John Horton Conway, bulmacalar ve oyunlar icat etmekten çocuksu bir zevk alırdı. Matematiğe olan tutkusu büyük ölçüde bu oyunlara ve bulmacalara duyduğu ilgiden besleniyordu. Kıyamet algoritmasını (haftanın gününü zihinden hızla hesaplamanın bir yöntemi) ve ünlü Game of Life’ı icat eden de oydu.
Conway’in matematik dünyasına en büyük katkılarından biri de gerçeküstü sayılar oldu. İlk olarak 1972 civarında, Go masa oyununu analiz ederken keşfettiği bu sayılar, matematiksel evreni genişleten devrim niteliğinde bir kavramdı. Birkaç basit kuraldan yola çıkarak, hem sonlu hem de sonsuz tüm sayıları oluşturmanın yeni bir yolunu keşfetti. Sonuç olarak ortaya çıkan sistem, gerçeküstü sayı sistemi olarak adlandırıldı.
John Conway’in ortaya koyduğu gerçeküstü sayılar, adlarını hak edecek kadar sıra dışıydı. Bu sayı sistemi içinde, sonsuzu sonsuz ile toplamak ve hatta sonsuzun karekökünü almak bile mümkündü.
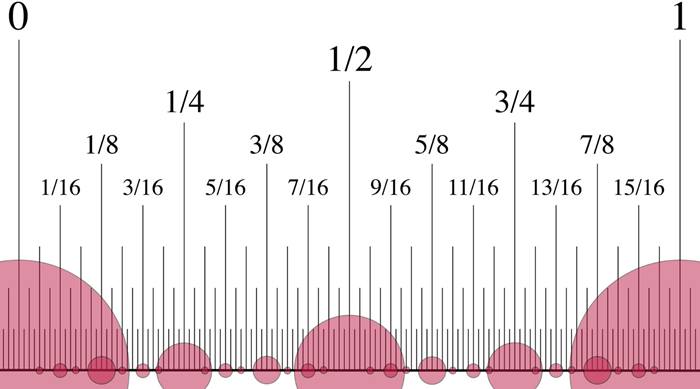
Gerçeküstü sayıların oluşturulması başlangıçta fazla da ilginç değildir. İki sayı seçersiniz ve ortasındaki sayıyı bulursunuz. Örneğin 0 ile 1 sayılarının ortasında 1/2 ve 0 ile 1/2 sayılarının ortasında 1/4 vardır. Bu işlemi devam ettirdiğinizde olağan dışı bir durum ortaya çıkar. Yeterince büyük sayılara ulaşıldığında, gerçek sayılar kümesinde bile bulunmayan yeni değerler oluşmaya başlar

Conway, gerçeküstü sayılar için iki temel kural belirledi. Her sayı, iki küme (ML ve MR) ile tanımlanır ve şu biçimde gösterilir. x = {ML : MR} (Burada ML soldaki, MR ise sağdaki küme anlamına gelir.)). İlk kural, soldaki kümenin elemanlarının her zaman sağdaki kümedekilerden daha küçük olmasıydı. Soldaki kümenin tüm elemanları, sağdaki kümedeki her şeyden küçük olmalıdır. Ayrıca, 0 bu iki küme arasında bir sınır görevi görür.
Gerçeküstü Sayılar Nasıl Oluşturulur?
Donald Knuth, gerçeküstü sayıları tanımlarken farklı bir gösterim biçimi kullanmayı tercih etti. Kitabında, 0 sayısını şu şekilde tanımladı: 0={ : }. Bu tanıma göre, diğer sayıların gösterimi şu şekildedir.
- 1 = {0: }
- -1 = { :0}
- {0:1} ise, 0 ile 1 arasında kalan sayı yani 1/2
- {1: } = 2
- {–1:0} = –1/2
- { :–1} = –2
Bu yöntemi devam ettirdiğinizde, tüm tam sayıları ve paydaları 2’nin kuvvetleri olan kesirleri elde edebilirsiniz. Ancak şu ana kadar diğer kesirleri, köklü sayıları ve π gibi irrasyonel sayıları üretemedik. İşte burada gerçeküstü sayıların en heyecan verici özellikleri devreye giriyor: ω ile tanışıyoruz.
Matematikte sonsuzluk, sayılabilen ve sayılamayan olmak üzere ikiye ayrılır ve ω sembolü, sayılabilir bir sonsuzluğu temsil eder

- Sayılabilen sonsuzluk: Doğal sayılar (1,2,3,…) bu gruba girer. Eğer sonsuz bir zamanınız olsaydı, bu sayıları teker teker sayabilirdiniz.
- Sayılamayan sonsuzluk: Gerçek sayılar (R) bu gruba girer. Herhangi bir yöntemle tek tek saymak mümkün değildir, çünkü iki sayı arasında sonsuz tane başka sayı bulunur.
İşin İçine Sonsuzluk Karışınca Gerçeküstü Sayılar Garipleşmeye Başlar
Artık irrasyonel sayılara geçebiliriz. Örneğin, √2, gerçeküstü sayı sisteminde şu şekilde yazılır.
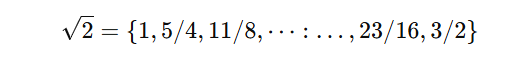
Bu yöntemle, π gibi diğer irrasyonel sayıları da tanımlamak mümkündür. Ancak gerçeküstü sayıların en ilginç özellikleri de tam olarak bu noktadan sonra ortaya çıkmaya başlar. Şimdi sonsuzluk kavramını tanımlayalım. Bunu yapmak için, Sayma sayılarını (1, 2, 3, …) soldaki kümeye yerleştirip, sağdaki kümeyi boş bırakalım. Bu durumda sonsuzluk şu şekilde olacaktır.
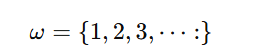
Bu ifade, tüm doğal sayılardan büyük olan bir sayıyı temsil eder. Sağ küme boş olduğu için, buraya eklenen her şey sonsuzdan daha büyük olacaktır. Eğer bu kavram size ilginç geldiyse, daha da garip bir keşif yapabiliriz. Şimdi soldaki kümeye yalnızca 0’ı ekleyelim ve sağ tarafta 1, 1/2, 1/4 gibi değerler bulunsun. Böylece ε (epsilon) adı verilen yeni bir sayı elde ederiz.
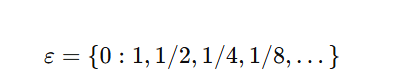
Bu epsilon, sonsuzluğun tersi olsun. Öyle küçüktür ki, onu temsil edecek hiçbir gerçek sayı yoktur. Bunun anlamı şudur: Gerçek sayılar kümesinde tanımlanamayan sonsuz küçük bir sayı elde ettik! Bu durumda sonsuz küçük bir sayı ile bir rasyonel sayıyı toplamak artık mümkündür.
Ayrıca ω + 1 ve ω – 1 gibi iki yeni sonsuzluklar da elde edebiliriz. Diğer bir deyişle sonsuzluk ile işlem yapmaya başlarız. Hayal gücümüz yardımı ile ortaya çıkan sayılar artmaya devam eder. Bu sayıları toplu halde resmetmeye çalışsak aşağıdaki gibi gözükecektir.
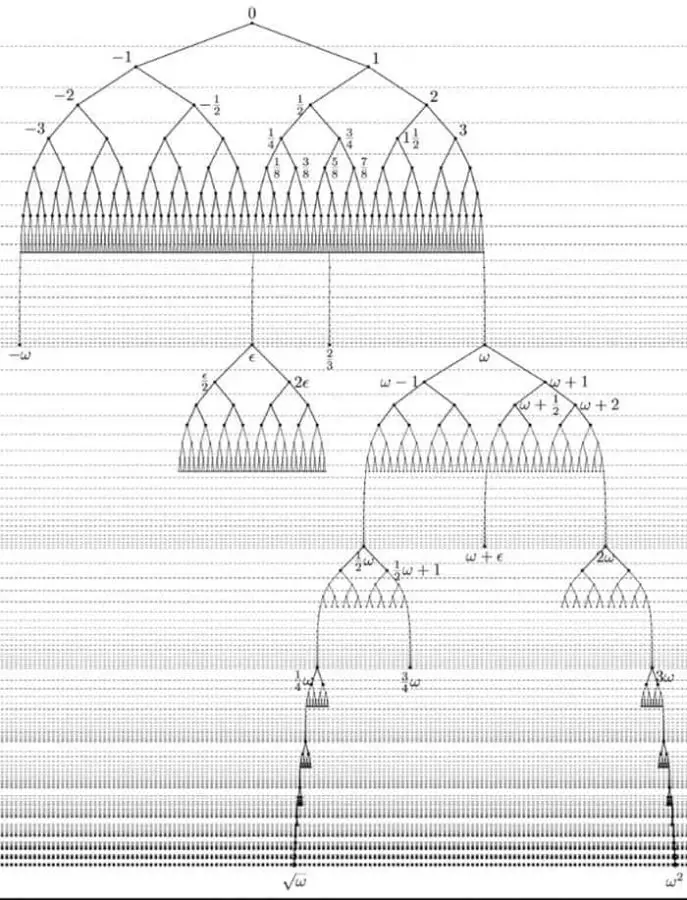
Sonuç Olarak
Bu yazı, gerçeküstü sayılara giriş niteliğindedir, ancak bu sayı sistemi daha pek çok sürpriz barındırmaktadır. İlginç bir şekilde, gerçeküstü sayıların sayısı, gerçek sayılardan çok daha fazladır, ancak bu sayılar sürekli bir yapı oluşturmaz. Eğer gerçeküstü sayıları bir sayı doğrusu üzerinde göstermeye çalışsaydık, aralarında boşluklar kalırdı. Bunun nedeni, mevcut sayıların arasına her zaman daha küçük sonsuz küçüklerin eklenebilmesidir.
Her ne kadar gerçeküstü sayılar soyut ve alışılmadık görünse de, Donald Knuth, bu sayı sisteminin dünyamızı tanımlamak için bildiğimiz diğer sayılar kadar uygun olduğuna inanıyordu. Ona göre: “Eğer insanlar yüz yıl boyunca bunu okulda öğrenmiş olsaydı, sayıların bu şekilde olduğunu düşünürlerdi.”
Sayıların insan zihninin bir ürünü olduğunu bildiğimize göre, Knuth’un bu sözünün doğru olabileceğini düşünmemek için bir sebep yok. Aslında, fizikçiler gerçeküstü sayıları teorilerine dahil etmeye çalıştılar. Ancak şimdilik, bu girişimler somut bir sonuç vermedi. Yine de, matematik ve fizik sürekli gelişen alanlardır ve gelecekte bu sayı sisteminin nasıl bir rol oynayacağını tahmin etmek zor.
Kaynaklar ve ileri okumalar
- Knuth, Donald Ervin. “Surreal numbers : how two ex-students turned on to pure mathematics and found total happiness : a mathematical novelette.” (1974).
- Surreal Numbers Are a Real Thing. Here’s How to Make Them. Yayınlanma tarihi: 14 Şubat 2024. Kaynak site: SCientific American. Bağlantı: Surreal Numbers Are a Real Thing. Here’s How to Make Them
- Nieto, Juan. (2016). Some Mathematical and Physical Remarks on Surreal Numbers. Journal of Modern Physics. 7. 2164-2176. 10.4236/jmp.2016.715188.
Matematiksel