Modüler aritmetik ifadesini daha önce hiç duymamış olabilirsiniz, ancak onu her gün en ufak bir zorluk çekmeden kullanıyorsunuz.

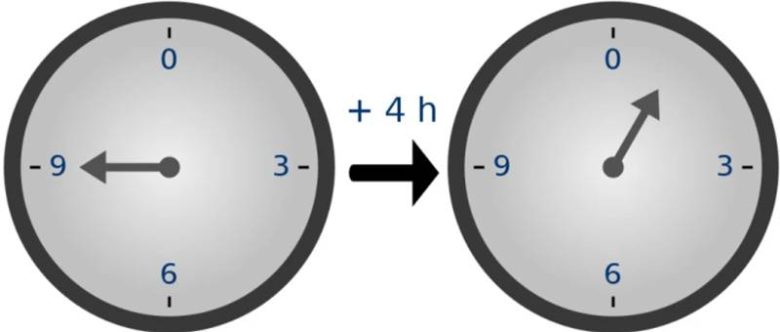
Bu sistemde sayılar, modül adı verilen belirli bir büyüklüğe ulaştıklarında başa döner. Farkındaysanız saatleri hesaplarken de 12’ye kadar sayar ve sonra tekrar birden başlarız. Örneğin sabah saat 08:00 iken 6 saat sonra saatin kaç olacağını bilmek istediğimizi düşünelim. Bulacağınız cevap 14:00 olacaktır. Yani öğleden sonra 2.
Bu esnada yaptığınız aslında bir modüler matematik hesaplamasıdır. Modülünüz ise 12 sayısıdır. Bunu da 8+6=14 ve 14≡2 (mod 12) biçiminde gösterebiliriz. Modular aritmetik ile yaptığımız işlemlerin diğer aritmetik işlemlerden farkını göstermek için sembol olarak denklik sembolünü “≡” kullanmamız önemlidir.
Benzer bir durum, haftanın günleri için de ortaya çıkar. Diyelim ki bugün günlerden Perşembe. Bugünden 1000 gün sonra haftanın hangi günü olacaktır? Bu sorunun cevabını bulmak için tek tek günleri saymanıza gerek yoktur. Yapmanız gereken sadece 1000 sayısını yediye bölüp kalanı bulmaktır. Bu işlemi yaparsanız kalanınız altı olur. Bu durumda sadece altı gün saymanız yeterlidir. Bu işlemi yaparsanız bugünden 1.000 gün sonra, günlerden Çarşamba olacağını kolayca bulabilirsiniz.
Yukarıdaki işlemde farkında olmadan modüler aritmetik kullanmış olursunuz. Günleri hesaplarken modülünüz yedi idi. Benzer bir mantıkla modülü 12 alarak ayları da hesaplayabilirsiniz. Kısacası biz fark etmesek de zaman ile ilgili hemen hemen her hesaplamada modüler aritmetik kullanırız.
İki sayı a ve b, 10’a bölündüğünde aynı kalanı veriyor ise, bu sayıları a ≡ b (mod 10) biçiminde yazabiliriz. Daha genel olarak, a ve b sayıları m’ye bölündüğünde kalanları aynıysa a ≡ b (mod m) biçiminde gösterilir. Genel olarak, a ≡ b (mod m) gösterim biçimi, ( a – b )’nin m’ye bölünebildiği veya m’nin katı olduğu anlamına gelir.
Her Taşın Altından Gauss Çıkıyor
Modüler aritmetik, Carl Friedrich Gauss tarafından başyapıtı Disquisitiones Arithmeticae adlı eserinin ilk sayfasında tanıtıldı. Gauss bu kitabı henüz 21 yaşındayken tamamladı ve üç yıl sonra 1801 yılında da yayınlandı. Bu çalışma, önceki birçok çalışmayı bir araya getirerek sayı teorisinde devrim yarattı.
Latince yazılmış son matematiksel metinlerden biriydi. Bu kitaptan önce sayılar kuramı, birbirinden ayrı duran teorem ve varsayımlardan oluşuyordu. Gauss, bu sonuçları derleyip toparladı, boşlukları doldurdu, eksik ve yanlış kanıtları düzeltti ve kendi katkılarıyla konuyu pek çok açıdan geliştirdi.

Modüler Aritmetik Ne İşe Yarar?
Modüler aritmetik, sayı teorisinin temel taşı olduğu saf matematikte yaygın olarak kullanılmaktadır. Ama aynı zamanda birçok pratik uygulamaya da sahiptir. Örneğin Uluslararası standart kitap numaraları (ISBN) her biri bir tire ile ayrılmış, değişken uzunlukta beş kısma bölünmüştür ve son bölüm kontrol basamağı olarak bilinir. Bu kontrol basamağı modüler aritmetik yardımı ile hesaplanır.

Bu kadar da değil. Kredi kartı ile alışveriş yapmak istediğiniz zamanlarda bir çoğumuz kart numaramızı yanlış gireriz. 1954’te IBM’de çalışan bir bilim insanı olan Hans Peter Luhn tarafından tasarlanan Luhn Algoritması yaptığımız bu hataları bulup düzeltmemize yarar.
Bu sistem de temelde modüler aritmetik üzerine kuruludur. Aslında şifreleme ile ilgili hemen hemen her uygulama modüler aritmetikten bir biçimde yararlanmaktadır.
1967’de matematikçi Robert Langlands, matematiğin iki ana ve görünüşte bağlantısız alanı olan sayı teorisi ve harmonik analiz arasında bir dizi bağlantı olduğunu ortaya koydu. Sayı teorisi, tam sayıların, özellikle asal sayıların matematiğidir. Harmonik analiz dalga formlarının matematiksel olarak incelenmesidir.
Fark ettiğiniz gibi bu alanlar birbirinden ayrık gibi görünmektedir. Ancak Langlands Programı birbirinden ayrık gibi gözüken bu iki yapıyı birbirine bağlar. Langlands’ın varsayımları, sayı teorisindeki problemlerin harmonik analiz dilinde yeniden çerçevelenmesine izin vermeleri bakımından önemlidir. ( Konu hakkında detaylı bilgiyi bu yazıda bulabilirsiniz.)
Bu bilgiyi bu yazıya eklememizin nedeni de temelde Langlands Programının modüler aritmetik ile bağlantılı olmasıdır. 1994’te Andrew Wiles, Fermat’ın son teoremini çözmek için Langlands’ın varsayımlarından birini kullanmıştır.
Son Olarak Ufak Bir Ek Bilgi
Matematikte bazı şeyleri ezberleriz ancak arka plandaki fikri genelde fazla da sorgulamayız. Bunlardan bir tanesi 9 ile bölünebilme kuralında karşımıza çıkar. İlkokul yıllarından beri bildiğimiz bir bilgi, verilen bir sayının 9 ile bölünüp bölünemediğini kontrol etmek için rakamları toplayıp sonucun 9’un katı olup olmadığına bakmaktır. Tahmin etmiş olabileceğiniz gibi bu işlemin de aslında modüler matematik ile ilişkisi vardır. Nasıl mı?
12345678 sayısını ele alalım. 9’a tam bölünür mü? Hemen rakamlarının toplamına bakalım. Toplam 36 yapıyor. Bu sayı 9 ile tam bölündüğü için verdiğimiz sayı da tam bölünüyor. Çünkü aslında şu işlemi yapıyoruz. 12345678 = 1.107 + 2.106 + 3.105 + 4.104 + 5.103 + 6.102 + 7 .10 + 8
Ancak, 10 ≡ 1 (mod 9); 102 ≡ 1 (mod 9); 103 ≡ 1 (mod 9) ve genel olarak 10k ≡ 1 (mod 9) olduğu bilgisine sahibiz. Bu durumda, 12345678 ≡ (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 ) (mod 9) biçiminde düşünebiliriz. Oldukça basit ancak son derece faydalı bir düşünce…
Kaynaklar ve ileri okumalar:
- Modular arithmetic: you may not know it but you use it every day. Yayınlanma tarihi: 2 Kasım 2017; Bağlantı: https://www.irishtimes.com/
- Fun With Modular Arithmetic; https://betterexplained.com/
Matematiksel