Bir Tarihin Hangi Güne Denk Geldiğini Nasıl Hesaplarız?

Bazen bir tarihin haftanın hangi gününe geldiğini bilmeniz gerekir. Elbette bunun için telefonunuzu açıp takvime bakmanız mümkündür. Ancak basit bir algoritma ve elbette matematik sayesinde bunu aklınızdan da söyleyebilirsiniz.

Lewis Carroll, Alice Harikalar Diyarında gibi edebi eserler yazmadığı zamanlarda matematikle uğraşıyordu. Çalışmalarından bir tanesi de bir takvim algoritmasıydı. Carroll, takvim algoritmasını kafasında uygulayarak belirli bir tarih için haftanın gününü yaklaşık 20 saniyede hesaplayabiliyordu.

Uzun yıllar sonra Scientific American köşe yazarı Martin Gardner, Carroll’un takvim algoritmasını okudu. Daha sonra Gardner, arkadaşı John Horton Conway’e Carroll’un algoritmasından bahsetti ve Conway’e daha basit bir algoritma bulabileceğini iddia etti.

Dünya çapında bir matematikçi olan Conway gerçekten 1973 yılında çok daha basit bir algoritma geliştirdi. Algoritmasına “kıyamet kuralı” (doomsday rule) adını verdi. Daha sonra bu kuralın adı günümüze kıyamet günü algoritması olarak ulaştı. İlk okunduğunuzda biraz zor gibi gelse de biraz pratik ile hızlı bir biçimde siz de haftanın istediğiniz gününü hesaplayabilirsiniz. Ayrıca bu konu okulda modüler matematik öğretirken de eğlenceli bir çalışma olacaktır.

Kıyamet günü algoritması basittir ve yalnızca temel aritmetik içerir. Dahası, çok az ezber gerektirir. Ayrıca ekleyelim, kıyamet günü algoritmasının kıyametle hiçbir ilgisi yoktur. Sadece bu seçim, Conway’in belirli bir yılda haftanın belirli bir gününün ilginç bir özelliğini keşfettikten sonra takvim algoritmasını adlandırma tercihidir.

Takvimimiz Her 400 Yılda Bir Kendini Tekrar Eder

Çoğu zaman bir yıl 365 günden oluşur. Ancak kimi zamanlarda bir yılda 366 gün olur. Bu yılları da artık yıl olarak isimlendiririz. 2024 sayısı 4’e kalansız biçimde bölündüğü için bir artık yıldır. Sonrasında 2028, 2032 yılları da artık yıl olacak ve bu ilişki 2100 yılına kadar devam edecektir.

Ancak 2100 yılında bizden sonra gelen nesil 4 ile bölünebilmesine rağmen bu fazladan günü eklemeyecektir. Artık yılları 4’e bölünebilen yıllar olarak düşünüyoruz. Ancak 1582’de Papa III. Gregory’nin yeni takvimimiz için getirdiği bir istisna vardır.

Gregoryen takviminde sonu çift sıfır ile biten yılların hepsi, 4 ile bölünmelerine rağmen, artık yıl değildir. Örneğin 1900 artık yıl değildi benzer biçimde 2100 de olmayacaktır. Ancak 2000 yılı artık yıldır. Çünkü bir diğer kural da 400’e bölünebilen yılların artık yıl olmasıdır.

Bunun bir sonucu olarak Miladi takvim ya da Gregoryen takvimi, her 400 yılda bir kendini tekrar eder. Yani her 400 yılda bir takvim haftanın aynı günü ile başlar. Her normal yılda, 1 Ocak günü bir gün ileri kayar. Ancak artık yıllarda iki gün ileri kayacaktır. Örneğin 6 Haziran 2023 günü Çarşamba ise, 6 Haziran 2024 günü Perşembe olacaktır. Ancak arada artık yıl varsa 1 değil, 2 günlük kaydırma yapma gerekecektir.

Kullandığımız takvimde dört yüz yıllık bir süre içinde 97 artık yıl ve 303 normal yıl vardır. Bu da 303+97+97=497 yapar. Bu sayı 7’nin tam katıdır. ( Burada 7 sayısı bir haftanın içindeki gün sayısıdır.) Bunun bir sonucu olarak da 1 Ocak her 400 yılda bir aynı güne denk gelir. Şimdi tüm bunları toparlayalım.

Bir Tarihin Hangi Güne Denk Geldiği Nasıl Hesaplanır?

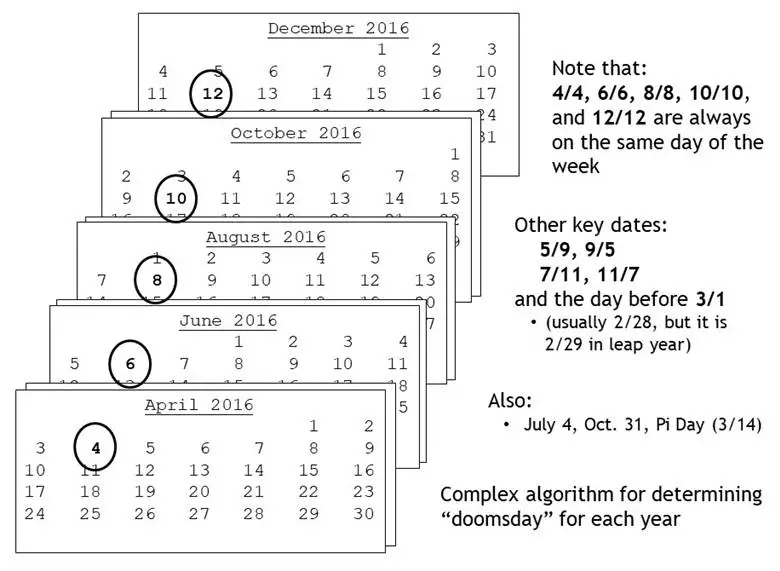
Kıyamet günü algoritmasının ardındaki temel fikir, belirli tarihlerin herhangi bir yıl içinde her zaman haftanın aynı gününü paylaşmasıdır. Örneğin 2023 yılında 4 Nisan, 6 Haziran, 8 Ağustos, 10 Ekim ve 12 Aralık günlerinin hepsi Salı gününe denk gelir.

İsterseniz takvime bakıp kontrol edebilirsiniz. 2024 yılında da bu tarihlerin hepsi Perşembe gününe denk gelecektir. Bu nedenle 4/4, 6/6, 8/8, 10/10 ve 12/12 tarihlerini merkez gün olarak kabul edilir. Bu tarihler akılda tutulmalıdır. Tarih hesaplamak için ilk olarak yüzyılların merkez günlerini bulmamız gerekiyor. Referans olarak da en yakın yüzyıl seçilir. Şu an en yakın yüzyıl 2000 yılı. Bu nedenle onu referans olarak seçelim.

2000 yılının Merkez Günlerine (4/4, 6/6 …) bakarsanız bu tarihlerin Salı günü olduğunu göreceksiniz. Aşağıdaki çizelgede diğer merkez günleri görebilirsiniz. Çizelgede Pazar: 0, Pazartesi:1, Salı:2, Çarşamba:3, Perşembe:4, Cuma:5, Cumartesi:6 biçiminde numaralandırılmıştır.

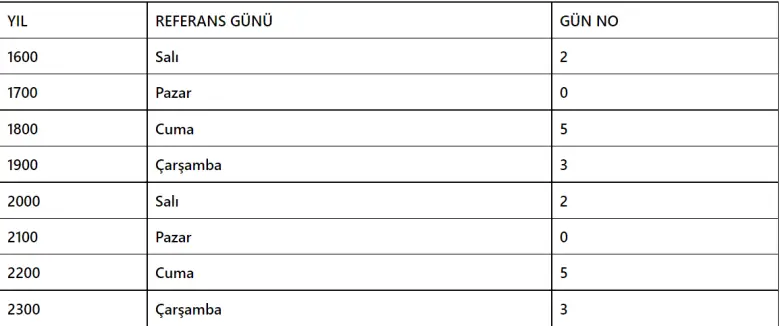
Bu sayılara 7’nin katları ilave edildiğinde gene aynı güne denk gelmelidir. Örneğin Cuma gününün kodu 5’tir. 7’nin katı olan 21 eklediğiniz de 21+5=26 ayın 26’sı da Cuma günü olmalıdır.

Bu durumda 400 yıl geri gidersek 1600 yılının merkezi günü de Salı günüdür. 1610 yılı için merkez günleri bulalım. Bu durumda 10 yıl geçtiğinde 10 günlük kayma olacaktır. Ancak unutmayalım aynı zaman da 4 yılda bir artık yıl olduğu için toplam 12 gün kaydırmamız gerekiyor. ( 4. ve 8. yıl için 2 yıl kaydırdık).

Hangi Tarihin Hangi Güne Denk Geldiğini Bulmaya Çalışalım

Şimdi gelin 29 Ekim1923 tarihinin hangi güne denk geldiğini bulalım. Referans olarak yine merkez günü Salı olan 2000 yılını alalım. 1923 ile 2000 yılı arasında 77 yıl var. Bu 77 yıl içinde de 77/4=19 kez artık yıl var. Bu durumda toplam 77+19=96 gün geriye gitmemiz lazım.

Bunu tek tek saymamıza gerek yok. 96 sayısının içindeki haftaları atalım ve geriye kalana bakalım. Bunu yapmak için 96 sayısını 7’ye bölüp kalanı bulmamız yeterlidir. Geriye kalan sayı 5 olacaktır. Bu durumda merkez günümüzden geriye 5 gün gitmemiz gerekiyor.

Ulaşmak istediğimiz 29 Ekim tarihine en yakın merkez gün 10/10 yani 10 Ekim olacaktır. 2000 yılında 10 Ekim tarihinin Salı günü olduğunu biliyoruz. Ancak 5 gün geriye gittiğimiz zaman 1923 yılında 10 Ekim Çarşamba günüdür.

Şimdi yapmamız gereken şey Çarşamba gününün üzerine 19 gün saymaktır. Bunun için de tek tek saymaya gerek yok. 19 günün içindeki haftaları atıp kalan sayıyı eklememiz yeterli. 19’un 7 ile bölümünden kalan 5 olduğuna göre Çarşamba gününe beş ekleyerek Pazartesi gününe erişiriz. Bu durumda 29 Ekim 1923 tarihi Pazartesi gününe denk gelmiştir.

Son olarak aklınıza şöyle bir soru gelebilir. Tamam 4/4, 6/6, 8/8, 10/10 ve 12/12 tarihlerini ezberlemek kolay ama ya aradaki aylar için ne yapmalı? Belki fark etmişsinizdir 5/9, 9/5, 7/11 ve 11/7′de aslında hep aynı güne denk gelir. Mesela 2023 yılı için bugünler Salıdır. O zaman diğerlerinin yanında bu tarihleri de akılda tutmak iyi olacaktır.

Sonuç olarak

Gördüğünüz gibi bir tarihin hangi güne denk geldiğini bulmanız için çok az ezber ve biraz da modüler matematik bilmeniz yeterlidir. Bu arada bu yazıda bahsettiğimiz takvimin hangi güne geldiği hesaplamasına bir çok farklı yaklaşım vardır. Hepsi bir miktar ezber gerektirir ancak sonuçları etkileyicidir.

Kaynaklar ve ileri okumalar

• What Day Is Doomsday? How to Mentally Calculate the Day of the Week for Any Date; Yayınlanma tarihi: 18 Ekim 2011. Kaynak site: Scientific American. Bağlantı: What Day Is Doomsday? How to Mentally Calculate the Day of the Week for Any Date;/
• On what day of the week were you born? Kaynak site: Math Plus Magazine. Yayınlanma tarihi: 1 Mart 2024. Bağlantı: On what day of the week were you born?

Matematiksel