Hepimizin tanıdığı çubuk grafiği, dikdörtgen çubuklar kullanarak verileri temsil etmenin özel bir yoludur. Çubuk grafikleri her yerdedir çünkü anlaşılmaları kolaydır. Gözlerimiz, uzunlukları hızlı bir şekilde karşılaştırabilir ve mesafeleri değerlendirebilir. Ancak bir sorun var. Çubuk grafiklerindeki verileri çoğumuz yanlış anlıyor olabiliriz.
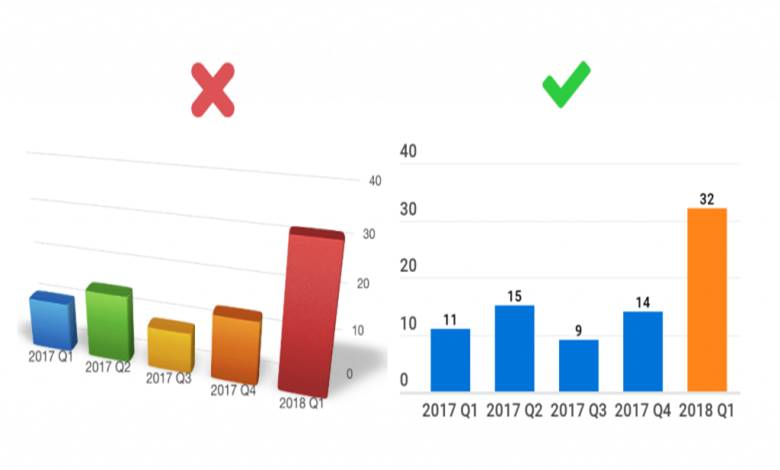
Wellesley College’ın Journal of Vision dergisinde yayınlanan bir araştırma, beş kişiden birinin çubuk grafiklerin göstermeyi amaçladığı verileri yanlış anladığını buldu. Çalışma, tamamen aynı grafiğe bakan kişilerin, temsil ettiği gerçekleri tamamen farklı anlayışlarla algıladığını gösteriyor. Bu çalışma, çubuk grafiklerin net iletişim araçlarından biri olmadığını ortaya çıkardı. İlginç olan bulgulardan biri, yapılan hatanın değişik milletler arasında yaş, cinsiyet, eğitim seviyesinden bağımsız eşit derecede yaygın olarak gözlemlenmesiydi.
Ortak yazar Doç. Dr. Jeremy Wilmer , “Ortalama değerleri gösteren çubuk grafikler siyasette, bilimde, eğitimde ve tıpta olmak üzere her yerde bulunur. İklim değişikliği, halk sağlığı ve ekonomi dâhil olmak üzere çok çeşitli konularda veri iletmek için kullanılır” diyor ve ekliyor. “Bunun gibi alanlarda netlik eksikliği, kamu söylemi üzerinde geniş kapsamlı olumsuz etkilere sahip olabilir.”

Çubuk Grafiklerini Neden Yanlış Anlıyoruz?
Çubuk grafiği temelde veri noktalarının dağılımını göstermek için kullanılmaktadır. Bir çubuk grafiği, sayısal veriyi eşit genişlikte bölmelere gruplayarak gösterir. Her bölme yüksekliği o bölmedeki veri noktası sayısıyla eşleşen bir çubukla gösterilmektedir. Aşağıda aynı gibi gözüken ancak farklı şeyi gösteren iki çubuk grafiği görüyorsunuz.
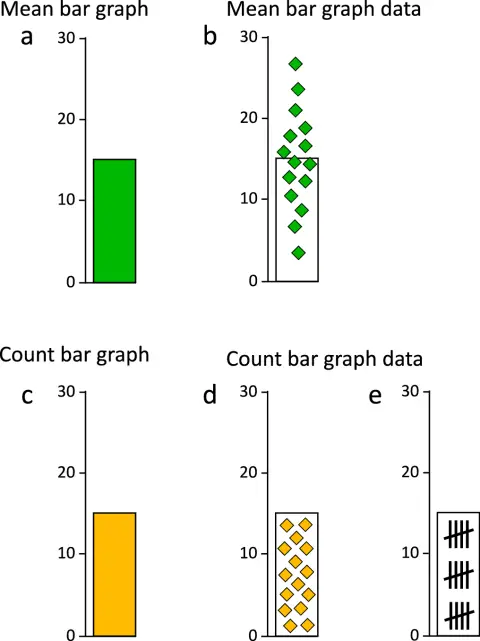
Görsel olarak birbirinin aynı olsa da üst satırdaki çubuk grafiği ortalamalar sonucunda ortaya çıkmıştır. Ortalamayı hesaba katarak çizilen bu grafikte çubuğun ucu ortalamadır. Oysa ki ikinci satırda karşımıza çıkan çubuk grafiği toplamı gösterdiğinden çubuk ucu, verilerin sınırıdır.
Gördüğünüz gibi birden fazla sayının ortalamasını göstermek için kullanılan bir çubuk grafiği ciddi kafa karışıklığına neden olmaktadır. Kendiniz bir uygulama denemek isterseniz, lütfen yanınıza bir kâğıt ve bir de kalem alın. Aşağıdaki maddeleri sırayla takip edin:
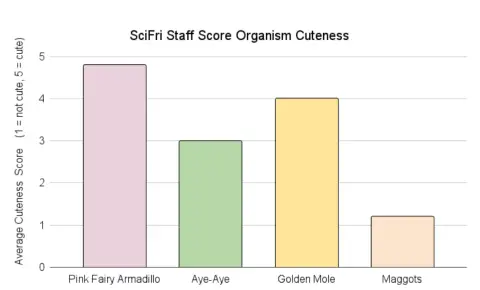
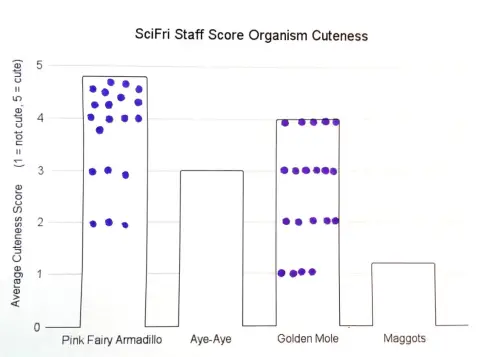
Yukarıdaki grafiğe göz atın. Bu görsel, dört hayvanın ortalama zekâ puanını gösterir. Her çubuğun bir ortalamayı temsil ettiğini unutmayın. Bu grafiği bir kâğıda çizin. En soldaki çubukta, o çubukta gösterilen değeri elde etmek için, ortalaması alınacak olası gözlem noktalarını gösteren 20 nokta çizin. Ardından, sarı çubuğu için de aynısını yapın. Çubuk grafik çiziminiz neye benziyor? Daha çok aşağıda verilen ilk resimdeki A gibi mi yoksa ikinci resimdeki B gibi mi?
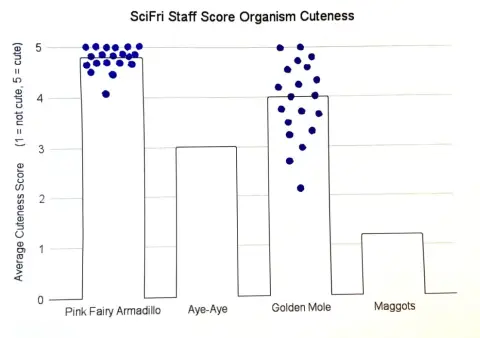
Araştırmacılarda çalışmalarında benzer bir süreç izlemişlerdi. Bir grup, ortalamanın doğru bir yorumunu resmettiler (şekil A). Şekil B’de çubuk uç sınır hatasını yapan diğer grubun çizimlerine aitti. Unutmayın ki bir ortalama değer grafiği, ortalamadan aşağıda ve yukarıda yer alan değerleri içermek zorundadır.
Tarihsel Süreçli Bir Hata
Bu çalışmadan alınacak önemli bir ders var. Bu da kimi durumlarda basitleştirmenin daha fazla kafa karışıklığına yol açabileceğidir. Sonucunda tek gözlem değerlerini, ortalama gibi bir özet istatistikle değiştirmenin tüm amacı, görsel gösterimi basitleştirmek ve okumayı kolaylaştırmaktır. Ancak bu basitleştirme, grafiğin gerçekte gösterdiği ortalama hakkında da kişiyi yanıltmaktadır.
Bilginin hızla yayıldığı ve yanlış anlamaların kamuoyu ve kamu politikası üzerinde derin bir etkisi olabileceği günümüzdeki gibi siyasi ve bilimsel bir ortamda, net veri iletişimi ve sağlam veri okuryazarlığı giderek daha önemli hale geliyor. Araştırmacılar, “Marketlerden doktor ofisine veya oy sandığına kadar, veriler karar alma mekanizmamızı etkiliyor. Çalışmamızın, verilerin anlaşılmasını geliştirmeye ve kurumlar ile bireyler tarafından bilinçli karar verme yolunu kolaylaştırmaya yardımcı olacağını umuyoruz.” diye belirterek konunun önemini hatırlatıyor.
Yazının devamında göz atmak isterseniz: İstatistikler Bilgilerini Yanlış Yorumlamanın 7 Büyük Günahı ve Bunlardan Kaçınma Yolları
Kaynaklar ve ileri okumalar:
- Kerns SH, Wilmer JB. Two graphs walk into a bar: Readout-based measurement reveals the. Bar-Tip Limit error, a common, categorical misinterpretation of mean bar graphs. J Vis. 2021 Nov 1;21(12):17. doi: 10.1167/jov.21.12.17. PMID: 34846520; PMCID: PMC8648051.
- Can You Read A Bar Graph? (Erişim Tarihi: 26.10.2022); https://www.sciencefriday.com/segments/bar-graph/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










