Kurt Gödel ve Eksiklik Teoremi: Cevabı Olmayan Sorular Vardır

Avusturyalı-Amerikalı mantıkçı, matematikçi Kurt Gödel matematiğin hem tutarlı hem de eksiksiz olamayacağını meşhur eksiklik teoremi ile gösterecekti.

Yaşadığımız dünya giderek daha zorlaşıyor ve her geçen gün daha da karmaşıklaşıyor. Yalanlar, gerçekler, tartışmalar ve belirsizlikler denizinde sanki bir kıyıdan diğer kıyıya sürüklenip duruyoruz. Neyse ki en azından matematik var.

Sonuçta matematik mutlak bir kesinlik anlamına gelir. Sorduğumuz her sorunun cevabını er ya da geç matematiğin içinde bulmamız mümkün olacaktır. Keşke, ancak ne yazık ki bu da mümkün değil. Bunun mümkün olmadığı gerçeğini Eksiklik teoremleri ile Kurt Gödel hatırlattı.

20. yüzyılın başlarında David Hilbert, matematik dünyasının çözmesi için 23 problem olduğunu ortaya koydu. Hilbert, matematikte belirsiz sonlardan, kanıtlanmamış öğelerden ve paradokslardan hoşlanmıyordu. Ne de olsa bahsedilen konu matematikti. Ancak ne yazık ki Kurt Gödel onun bu düşüncesinin imkansız olduğunu kanıtlayacaktı.

Kurt Gödel’in Eksiklik Teoremi Nedir?

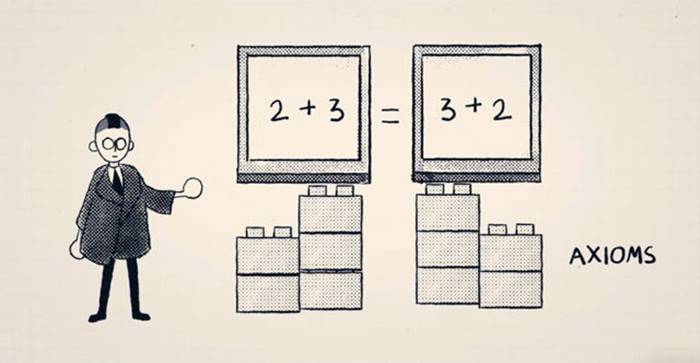
Her matematik önermesinin ispatı, doğru olduğu bilinen diğer önermeler temel alınarak yapılır. Bu ispatlar zincirinde en temelde yer alan önermelere aksiyom denir. Aksiyomlar, tüm matematiği üzerine kurduğumuz, doğru ve tutarlı olduğunu varsaydığımız, ancak ispatlayamadığımız önermelerdir.

Örneğin geometri öğrenirken ‘İki noktadan ancak ve ancak bir doğru geçer’ ifadesini temel bir doğru olarak kabul eder ve sonra karşılaşacak ilgili konularda bu temel veriyi kullanırsınız. Karşılaştığınız yeni durumları bunun üzerine teorem olarak inşa eder ve ispatını buna dayandırırsınız.

İşte bu mantık çok eskiden beri matematikçileri cezbediyordu. Tüm matematiği sağlam temellere oturtmak için “gerekli tüm aksiyomları” tanımlamak yeterliydi. Daha sonra bu aksiyomları kullanarak herhangi bir matematiksel önermenin doğruluğuna ya da yanlışlığına karar verilebilirdi.

Ancak Kurt Gödel, insan zihninin asla böylesine mükemmel bir matematiksel sistemi yaratamayacağını bizlere gösterdi. Sonucunda her zaman doğru olan ancak doğruluğu kanıtlanamayan ifadeler olacaktı.

1931 yılında bir Alman bilim dergisinde kısa ve ilgi çekici olduğu kadar da düşündürücü bir yazı yayınlandı. Yazının başlığı şöyleydi. ‘Uber Formal unentscheidbare Sâtze der Principia Mathematica’( Üzerinde kesin kararlar veremeyeceğimiz matematik prensipleri ve benzeri sistemler). Yazarı ise Viyana Üniversitesinden 25 yaşındaki Kurt Gödel idi.

Bu yazı yayınlandığında, hem yazının başlığı hem de içeriği çoğu matematikçi tarafından bilinmiyordu. Bu alanda yetkin az sayıda bilim insanı olması Gödel’in çalışmasının devrim niteliğinde sonuçlar doğurmasını gölgelemedi. Çünkü çalışma gerçekten temel felsefe alanında geniş ve etkin bir yer kaplıyordu.

Eksiklik Teoremi Tam Olarak Ne Diyordu?

Matematikte yapılması mümkün olan her şeyin büyük bir kutunun içinde olduğunu hayal edin. Matematiğin yapısı gereği bu kutunun içinde adına aksiyomlar dediğimiz, kanıtlanamayan veya çürütülemeyen bir dizi şey de olmak zorundadır.

Şimdi bu kutunun içindeki her şeye bir kod numarası verin. Doğru ya da yanlış olması fark etmez. Her şeyin kendine ait bir numarası olsun. Şimdi bu sayıları kullanarak matematiksel ispatlar hakkında konuşmaya başlayalım. ( Bu sayılara Gödel sayıları denir)

Şimdi, Epimenides yani Yalancı paradoksunu düşünün. “Tüm Giritliler yalancıdır.”cümlesini yorumlayın. Eğer “tüm Giritliler yalancıdır” önermesini doğru kabul edersek, kendisi de Giritli olan Epimenides‘in yalancı olması gerekir. Eğer Epimenides yalancıysa, tüm söyledikleri gibi, “tüm Giritliler yalancıdır” önermesinin de yanlış olması gerekir. Yani doğru söylediğine inanırsak yalan söylediğini anlıyoruz.

Eğer “tüm Giritliler yalancıdır” önermesi yanlış kabul edersek de bu sefer, kendisi de Giritli olan Epimenides’in doğru söylüyor olması gerekir. Şu halde, “tüm Giritliler yalancıdır” önermesi de doğru olmalıdır. Gördüğünüz gibi ortaya bir paradoks çıkıyor.

Gödel Eksiklik Teoremini İspat Ederken Yalancı Paradoksunu Örnek Verecekti

Gödel’in eksiklik teoremiyle başardığı da temel aritmetik kullanarak yalancı paradoksunun bir tür matematiksel versiyonunu oluşturmaktı. “Bu ifade kanıtlanabilir değil” cümlesini ele aldı. Bu cümlenin neden seçildiğini anlayabilirsiniz. Sonuçta bu ifadenin doğru olduğunu kanıtlayabilirseniz, o zaman yanlış olur! 

Yalnızca kanıtlanamazsa doğrudur. Bu haliyle, bu doğal sayılarla ilgili bir ifade değildir. Ancak Gödel, bunun gibi İngilizce ifadelere sayılar atamak için ustaca bir yol tasarlamıştı. Bu sayede de ifadenin doğru olup olmadığını bulmak için yapması gereken kutunun içine koyduğumuz aksiyomları kullanarak bu denklemi çözmekti.

Sonucunda sayı teorisinin aksiyomları içinde yukarıdaki cümleye karşılık gelen denklemin doğru olup olmadığını kanıtlamanın imkansız olduğunu kanıtladı. Sonrasında da “Bu teorinin aksiyomları birbiriyle çelişmez.” cümlesini ele aldı. Bunu sayısal koda dönüştürdü ve sonucun kanıtlanamaz olduğunu bir kez daha kanıtladı. 

Tıpkı yalancı paradoksundaki cümlenin doğru ya da yanlış olduğuna karar verilememesi gibi, Gödel’in eksiklik teoremi de ne kadar yeni aksiyom tanımlanırsa tanımlansın doğruluğuna ya da yanlışlığına “karar verilemeyecek” önermeler olacağını söyler.

Kurt Gödel Çoğu Kişi Tarafından Yanlış Anlaşılacaktı

Gödel’in Eksiklik teoremi matematiğin kusurlu olduğunu ortaya koymaya çalışmamıştı. Onun amacı bu değildi. Bu teorem aritmetiği kucaklayan herhangi bir tutarlı aksiyomatik sistemin eksik olduğunu belirtir. Eksik olmanın anlamı şudur. Mevcut sistem içinde bulunan aksiyomları kullanılarak bazı ifadeler ne kanıtlanabilir ne de çürütülebilir.

Gödel bir sistemin tutarlı olduğunu o sistemi kullanarak kanıtlayamayacağımızı bize gösterdi. Elinizde matematiksel bir önerme varsa ya doğru ya da yanlış olmasını beklersiniz çünkü hem doğru hem de yanlış olamaz.

Eğer bir aksiyom sistemi matematiksel önermelerin her durumda ya doğru ya da yanlış olduğunu gösteriyorsa sistemin “tutarlı” olduğu söylenir. Tutarlı aksiyom sistemleri kullanılarak mantık yürütme yoluyla bir önermenin hem doğru hem de yanlış olduğu sonucuna varılamaz. Bir sistemin doğruluk ve tutarlılığını ancak o sistemin dışındaki bir sistemle karşılaştırarak kanıtlanabilir.

Kaynaklar ve ileri okumalar

• The foundations of mathematics are unproven; yayınlanma tarihi: 30 Nisan 2021; Kaynak site: Big Think. bağlantı: The foundations of mathematics are unproven/
• Gödel and the limits of logic; Yayınlanma tarihi: 1 Haziran 2006; Kaynak site: Plus Maths. bağlantı: Gödel and the limits of logic;
• Gödel’s Incompleteness Theorem – Numberphile; yayınlanma tarihi: 31 Mart 2017; Bağlantı: https://www.youtube.com/

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel