Claude Shannon, bu web sayfası da dahil olmak üzere her türlü mesajın, bir dizi 0 ve 1 olarak iletilebileceğini fark eden ilk kişiydi. Bunun sonucunda da bilgi teorisi çalışma alanının kurucusu olarak adını tarihe yazdıracaktı.
Tek bir makalenin yepyeni bir araştırma alanına kapı açması çok sık rastlanan bir durum değildir. Ancak Claude Shannon’ın 1948’de yayınladığı ‘İletişimin Matematiksel Kuramı’ (The Mathematical Theory of Communication) adlı makalesini yayınladığında olan buydu.
Başlığı ilk başta garip gelebilir, çünkü iletişimi matematiksel olmaktan çok uzak olarak düşünürüz. Ancak Shannon makalesini yazarken, insanların birbirleriyle konuşmasını düşünmüyordu. Bunun yerine, telgraf, telefon, radyo ve televizyon gibi uzun mesafeli bilgi aktarmanın çeşitli yollarıyla ilgileniyordu.
Teorisi bu tür bir iletişim üzerine kuruluydu. Shannon, medya aracılığıyla iletebileceğiniz bilgi miktarını ölçmek istedi. Mesaj göndermenin birçok yolu vardır. Ancak Shannon gibi düşünmek için, bu yöntemlerin her birinin bir mesajı nasıl ilettiğini unutmak gereklidir.
Enformasyon – Bilgi Teorisi Nedir?
En temel haliyle, Shannon’ın bilgi entropisi, bir mesajı kodlamak için gereken ikili basamak sayısıdır. Bugün bu, bir mesajda ne kadar bilgi olduğunu tanımlamanın basit bir yolu gibi geliyor. Ancak 1948’de her türden bilginin bu şekilde sayısallaştırılması devrim niteliğinde bir adımdı.
Çok gürültülü bir yerde konuştuğunuzu varsayalım. Mesajınızın karşınızdaki kişiye iletildiğinden emin olmanın en iyi yolu nedir? Belki de birçok kez tekrarlamaktır. Sonucunda tekrarlama, gürültülü bir restoranda mesajının iletildiğinden emin olmak isteyen herkesin ilk içgüdüsüdür, ancak bu çok da verimli bir yol değildir. Sonucunda tekrarladıkça iletişimi güvenli hale getirirsiniz ancak bu süreçte de hızdan ödün verirsiniz.

Ancak Shannon, bir sinyalin bilgi içeriğini ölçmenin ve bilginin herhangi bir iletişim kanalı üzerinden güvenilir bir şekilde iletilebileceği maksimum hızı hesaplamanın bir yolunu bulmuştu. Üstelik tüm bunları, dünyada 10’dan az bilgisayarın olduğu bir dönemde yapmıştı.
Shannon’ın ifadesiyle bir mesajın bilgi içeriği, mesajın asıl anlamıyla değil, mesajı iletmek için gereken ikili sayı miktarıyla ilişkilidir. Bu açıdan bakınca, bilginin doğası ne olursa olsun -ister Shakespeare sonesi, ister Beethoven’ın Beşinci Senfonisi kaydı- onu iletmeden önce bitlere kodlamak, her zaman en verimli yoldur.
Örneğin bir radyo sisteminde, hem ilk ses hem de havadan gönderilen elektromanyetik sinyal analog dalga formları olsa da, Shannon’ın teoremleri, önce ses dalgasını bitlere sayısallaştırmanın ve sonra bu bitleri elektromanyetik dalgaya eşlemenin en uygun yol olduğunu ima eder.
Bilgi Teorisi Nasıl Çalışır?
İlk olarak Shannon, saniyede bilgiyi temsil edecek minimum bit sayısı için bir formül buldu. Bu sayıya entropi oranı H adını verdi. Bu sayı, kaynağın hangi mesajı üreteceğini belirlemede yer alan belirsizliği niceliksel olarak belirtiyordu.
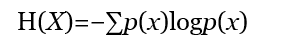
Entropi oranı ne kadar düşükse, belirsizlik o kadar az olur ve dolayısıyla mesajı da sıkıştırmak o kadar kolay olurdur. Örneğin, dakikada 100 İngilizce harf hızında mesajlaşma, her dakika 26100 olası mesajdan birinin gönderilmesi anlamına gelir. Tüm bu olasılıklar 470 bit olarak kodlanabilir. Bunun nedeni 26100 ile 2470 in birbirine yakın olmasıdır.
Shannon, bilgiyi tanımlamanın yanı sıra bir iletişim kanalı üzerinden bilgi gönderme yeteneğini de analiz etti. Bir kanalın aşılamayacak belirli bir maksimum iletim hızına sahip olduğunu buldu. Bugün buna kanalın bant genişliği diyoruz.
Shannon, düşük bant genişliğine sahip bir kanalda bile, iletim hızını kanalın bant genişliği içinde tutarak ve hata düzeltme şemaları kullanarak mükemmel, hatasız iletişimin elde edilebileceğini matematiksel olarak gösterdi.
Sonuç Olarak;
Bu şaşırtıcı sonuç, bitin evrensel bilgi para birimi olarak hüküm sürdüğü modern dijital bilgi çağının temel taşıdır. Günümüzdeki tüm sayısal iletişim teknolojileri; uydu iletişimleri, cep telefonu şebekeleri, internet, hepsi, Shannon’un bilgi teorisine dayanarak geliştirilmişlerdir.
Kaynaklar ve İleri Okumalar:
- Claude E. Shannon: Founder of Information Theory; Yayınlandığı Yer: Scientificamerican. Bağlantı: https://www.scientificamerican.com
- Information Theory: What relationship did Claude Shannon have with Alan Turing? Bağlantı: https://www.quora.com/
- How Claude Shannon Invented the Future. Yayınlanma tarihi: 22 Kasım 2020.; Yayınlandığı Yer: Quantamagazine.; Bağlantı: How Claude Shannon Invented the Future/
- Giannini, Tula & Bowen, Jonathan. (2017). Life in Code and Digits: When Shannon Met Turing. 10.14236/ewic/EVA2017.9.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel








