Bu yazımızda öpüşen sayılardan bahsedeceğiz. Ancak en başta söyleyelim. Konu aklınıza gelen ilk şey ile kesinlikle ilgili değil. Yazının içerisinde kaşınıza çıkacak öpüşme kelimesini temelinde temas etme biçiminde düşünmeniz gerekiyor.

Uzayda sabit noktadan eşit uzaklıktaki noktaların oluşturduğu cisme bildiğiniz gibi küre denir. Öpüşen sayı, merkezi bir küre etrafına birbirlerine ve ortadaki küreye değecek şekilde yerleştirilebilen aynı boyuttaki kürelerin sayısıdır.
Günümüzde bilardo oyununda kissing number ( yani öpüşen/ öpüşme sayısı) kelimesi bilardo toplarının birbiri ile kaç defa temas ettiğini belirlemede kullanılmaktadır. Bu ön bilgiyi verdikten sonra şimdi konumuza geri dönebiliriz.

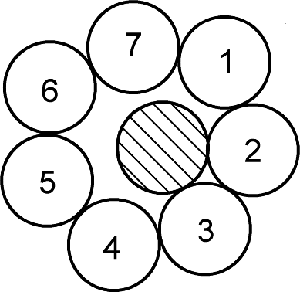
Öpüşen sayılar için iki boyutta elde edeceğiniz sayı altı olacaktır. Bunu bulmak için de cebinizdeki bozuk paralar ile yukarıdaki görseldeki basit deneyi yapabilirsiniz. Gördüğünüz gibi bir daireye sadece altı tane daire temas edebilmektedir. Bu nedenle de bir bilardo masasında en fazla altı top ortadaki bir topa dokunabilir. Yedinciye yer yoktur. Ancak üç ve daha ileri boyutta işler bu kadar kolay olmaz. Şimdi tarih zamanı…
Isaac Newton ve David Gregory Tartışması

1694’te, Cambridge Üniversitesinde o zamanın önde gelen iki bilim insanı olan Isaac Newton ve David Gregory arasında ünlü bir tartışma gerçekleşti. Anlaşmazlıkları yukarıda aktardığımız öpüşme sorunu ile ilgiliydi.
Diğer bir deyişle, Newton ve Gregory, merkezi bir topla temas ettirilebilecek aynı yarıçapa sahip kürelerin sayısı hakkında tartışıyorlardı. Ancak tartışmaları topları değil, merkezde duran bir güneşin etrafında dönen çeşitli büyüklükteki yıldızların dağılımını içeriyordu.
Bu tartışma sırasında, bir kürenin aynı büyüklükteki 13 başka küreyle temasa geçip geçemeyeceği sorusu ortaya çıktı. Ve fikirlerin ayrıldığı yer aslında tam da burasıydı. Newton öpme sayısının 12 olduğunu ileri sürdü. Gregory ise bu sayının 13 olduğunu söyledi.
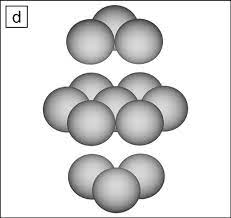
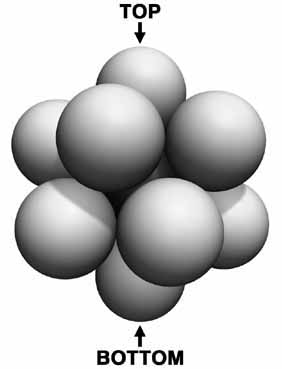
Bu sırada da işin içine Kepler karıştı. Çünkü Kepler üç boyutlu uzayda merkezdeki bir küreye dokunan 12 tane küre olacağını söylemişti. Aşağıdaki şekle bakarak bu 12 küreyi görebilirsiniz. Peki ama neden 13 olmasın ki?
Aslında 12 küreyi paketlemenin başka bir yolu da vardır. Bu paketleme biçiminin nasıl olacağını kafanızda canlandırabilmek için bir futbol topunun üzerindeki siyah karelerin yerleştirilişini düşünün. Bu durumda küreler aşağıdaki gibi görünür.
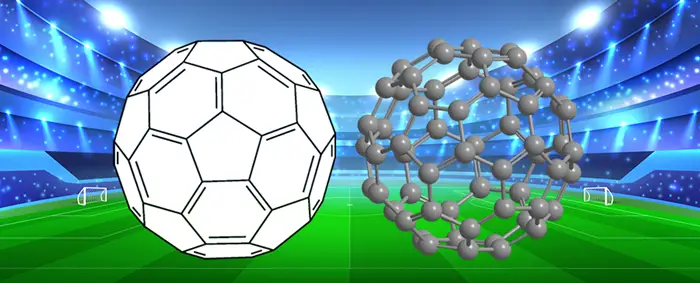
Bu tip bir paketlemeye ikozahedral düzenleme denir. Ancak bu tip bir düzenlemede 12 topun arasında boşluklar kalır. David Gregory bu boşluklara bir topun daha sığabileceğini düşünüyordu.
Öpüşen Sayılar Tartışmasını Kim Kazandı?
En sonunda Newton’un haklı olduğu ortaya çıktı. Bu nedenle, merkezdeki bir topa dokunabilen en fazla sayıda top günümüzde genellikle Newton sayısı olarak adlandırılmaktadır. Ancak yaşamları boyunca bu iki adam doğru cevabı asla bilemediler. Çünkü onların tartışmalarının çözümü ancak 1953 yılında Bartel Leendert van der Waerden tarafından formüle edildi.
Daha yakın zamanda, 2006 yılında, Oleg R. Musin tarafından modern bir ispat daha yapıldı. Detaylarda bulabileceğiniz bu ispatta öpüşen sayının kesinlikle 13 ten az olması gerektiği gösterildi. Anlayacağınız Newton bir kere daha kesinlikle haklıydı. Ancak sadece 3 boyutlu uzayda.
Çünkü 4 boyutlu uzayda öpüşme sayısı 24’tür. Boyut sayısı arttıkça da bu sayı artar. Ancak Newton elbette bunu bilemezdi. Yazının devamında okumaya devam etmek isterseniz: David Hilbert ve Çözülmesi Gereken 23 Matematik Problemi
Kaynaklar ve ileri Okumalar:
- Kissing Numbers – Numberphile; https://www.youtube.com
- George G. Szpiro; Kepler’s Conjecture: How Some of the Greatest Minds in History Helped Solve One of the Oldest Math Problems in the World; ISBN-10: 0471086010
- Musin, Oleg. (2006). The Kissing Problem in Three Dimensions. Discrete & Computational Geometry. 35. 375-384. 10.1007/s00454-005-1201-3.
- Twelve’s Company, Thirteen’s a Crowd; yayınlanma tarihi: 1 Ocak 2003; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel



