Tinder’den çok önce, bir çift ekonomist çöpçatanlık sorununu araştırdı ve romantizmin çok ötesinde uygulamaları olan bir formül buldu. Bu yazıda Gale ve Shapley’in kararlı evlilik problemine göz atacağız.

Aşk ve ilişki durumumuzu algoritmalar aracılığı ile düzenlemek mümkün mü acaba? Sürüp sürmediği bilinmese de araştırmalara göre günümüzde evliliklerin yaklaşık üçte biri internet ortamında başlıyor. Hatta bu iş için kurulu çöpçatanlık siteleri bile mevcut.
Peki bu siteler geri planda kimin için kimin doğru aday olduğunu nasıl bilebiliyor? Tahmin etmiş olabileceğiniz gibi cevap geri planda çalışan eşleştirme algoritmaları. Bu algoritmalar insanların profillerini tarayarak onların beğenilerine ve kişilik özelliklerine göre eşleşmelerini sağlıyor.

2012 yılında Nobel Ödülünü David Gale ve matematikçi Lloyd Shapley tarafından yaratılan bir eşleştirme algoritması aldı. Bu algoritma ile ilgili çalışmalar, ikilinin 1960’larda kolej başvurularıyla ilgili bir problemi çözmek istemesi ile başlamıştı. Her öğrencinin bir yer bulacağı daha da önemlisi ilk seçimlerini kazanamayan öğrencilerin bile mutlu olacağı bir yerleşim mümkün olabilir mi? Bu soru Kararlı Evlilik Probleminin (Stable Marriage Problem) başlangıcıdır.
Kararlı Evlilik Problemi Nedir?
Hemen bir örnek ile algoritmayı aktarmakta çalışalım. Diyelim ki bir çöpçatanlık sitesi işletiyorsunuz. 200 tane müşteriniz var. 100 erkek ve 100 kadın. Her kadın, size tercih sırasına göre sıralı 100 erkeğin bir listesini yaptı. Listenin başında en çok evlenmek istediği kişiler var ve sıralama en aza doğru gidiyor. Sonrasında benzer bir sıralamayı erkekler de yapıyor.
Keşke herkes listede kimi tepeye koyuyorsa, kendisi de o kişinin listesinin en üstünde yer alsa. O zaman ortada çözecek bir problem olmazdı! Ama hayat bundan daha karmaşık. Peki bu durumda çözümün nasıl olmasını istiyoruz? Şimdi her müşteriyi karşı cinsten bir üyeyle eşleştirmeniz ve hepsinin evlendiğinden ve sonsuza dek nispeten mutlu yaşadığından emin olmanız gerekiyor. Elbette bazı müşterileri ilk tercihleri ile evlenemeyecek.
Listedeki bir erkek, iki veya daha fazla kadın tarafından birinci sırada yazıldı ise, birileri daha azıyla yetinmek zorunda kalacak. Amacımız herkesi olabildiğince mutlu bir şekilde eşleştirecek bir formül bulmak. Bunun için eşleştirmemizin kararlı olması gerekiyor.
Kararlı Evlilik Problemi Nasıl Çalışır?

Şimdi üzerinde çalışması daha kolay olacağı için dört kadın ve dört erkek üzerinden bu eşleştirmeyi inceleyelim. Dört kadınımız (A, B, C, D) ve dört erkeğimiz ise (a,b,c,d) olsun. Öncelikle bu sekiz kişiye tercihlerini yazmalarını isteyerek işe başlayalım. Sonra da tercihleri incelemeye alalım. Amacımız herkesin bir eşi olacak biçimde, kadın ve erkeklerin ilk tercihleri olmasa bile ulaşabilecekleri en iyi seçeneğe göre eşleşebilmeleri.
Evlilik tekliflerini kadınlar yapsın. Mesela A’nın tercihleri (b, c, d, a); B’nin tercihleri (c, a, d, b); C’nin tercihleri (c, d, a, b) ve D’nin tercihleri de (c, b, a, d,) biçiminde olsun. Bu arada elbette erkeklerde kendi tercihlerini sıralamış durumda. Sıralamaya bakarsak “c” oldukça popüler.
Bunun sonucunda kendisine B, C ve D den 3 tane evlilik teklifi geldi. Bu durumda şimdi “c” nin listesine göz atalım (B, C, D, A) demek ki mutlu bir çift elde edebildik: (B,c) Sonuçta her ikisi de ilk tercihleri ile eşleşmiş oldu. Şimdi ret cevabı alan iki kadının ilk tercihleri listeden çıkartalım ve ikinci tura başlayalım.
A’nın yeni listesi (b, c, d, a); C’nin listesi (d, a, b); ve D’nin listesi (b, a, d) biçiminde artık. Ve tekrardan evlilik teklifi aşaması var. Gördüğümüz gibi bu turda da şanslı erkeğimiz “b”. Sonuçta iki kişiden teklif aldı yani A ve D. Hemen “b”nin tercihlerine göz atalım.
Onun listesi de (D, A, C, B) biçiminde olsun. Bu durumda yeni çiftimiz (D, b)’ye de mutluluklar dileriz. Şimdi ret edilen A’nın ilk tercihini çıkartalım ve bu biçimde devam edelim. Sonunda algoritma sona erer. Hepsi eşleşir ve sonsuza dek mutlu (ya da en azından bir istikrar içinde) yaşarlar. 4 kişi ile bile soru bu kadar zor iken bir milyon kişi için bu işi listeleme yolu ile çözüme ulaşmak imkansız gibi. Mecburen işin içine algoritmalar karışmalı.
Gale-Shapley Algoritması Başka Nerelerde Karşımıza Çıkıyor?
1980’lerde, Alvin Roth adında bir ekonomist, ekonomiye bir mühendislik disiplini gibi yaklaşmakla ilgileniyordu. Amacı gerçek dünyadaki sistemleri geliştirmek için teorik fikirleri kullanmaktı. Sonucunda Gale-Shapley algoritmasını farklı alanlara uygulamaya karar verecekti.

Algoritma ilk olarak ülke çapındaki hastanelere yeni doktorların atanmasını sağlayan bir sistemin alt yapısına uygulandı. Daha sonrasında da öğrencilerin tercih ettikleri okullara yerleştirilmesinde algoritma başarısını kanıtladı. Roth ve meslektaşları onu yeniden tasarlamadan önce, devlet lisesine atama süreci tam bir karmaşaydı. Yılda yaklaşık 30.000 öğrenci istemedikleri okullara gitmek zorunda kalıyordu. Ancak sonucunda herkesin daha mutlu olduğu atamalar olası olacaktı.
Asıl atılım 2004’te gerçekleşti. Roth, algoritmanın organ nakli hastalarının donör bulmasına yardımcı olacak şekilde kullanılabileceğini de fark etmişti. Roth, uyumsuz donör-alıcı çiftlerinin aynı durumda olan başkalarını bulmasına yardımcı olacak bir değişim sistemi tasarladı.
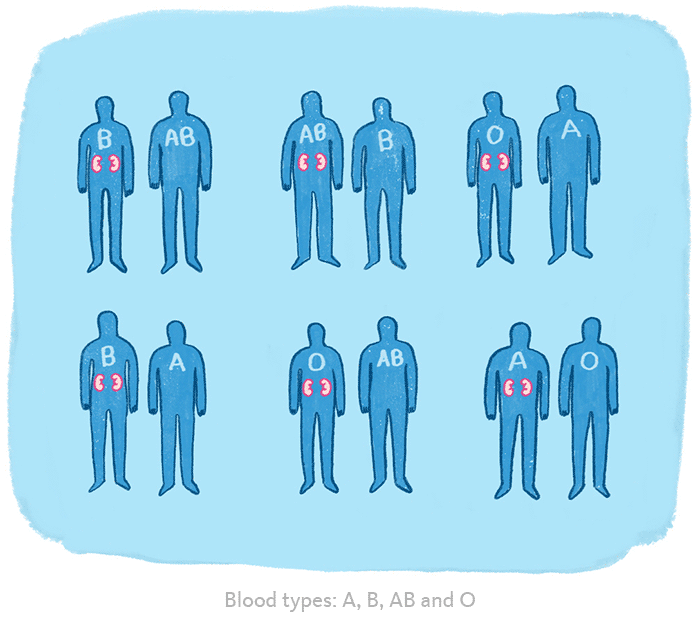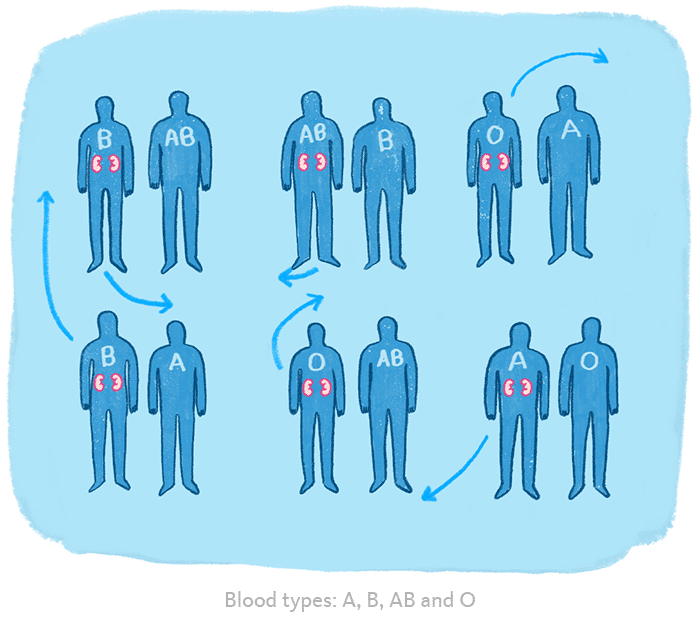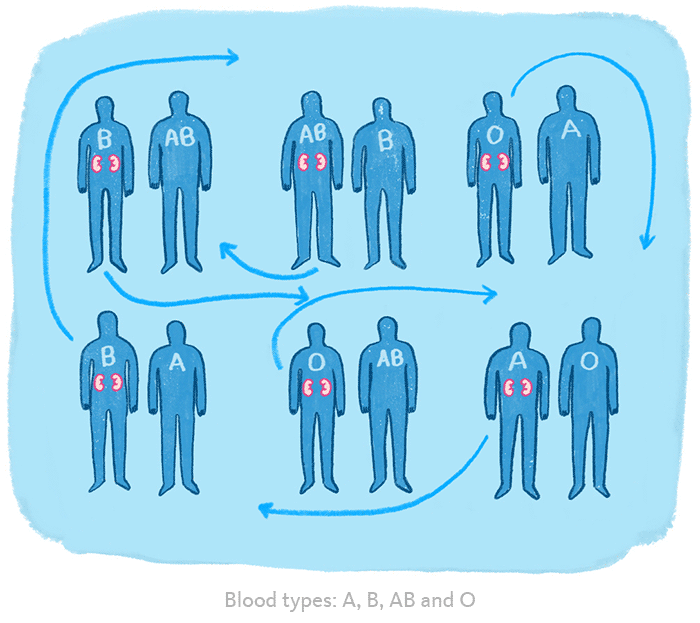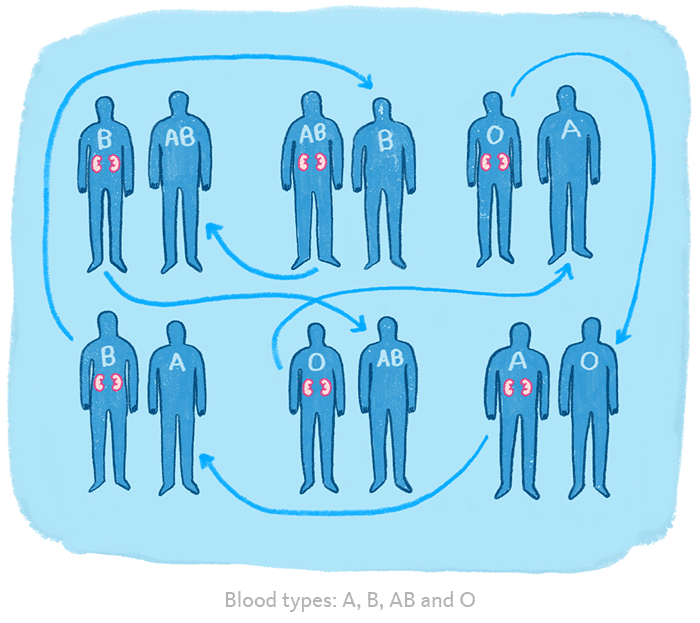
Bunun sonucunda on binlerce kişi uzun zamandır bekledikleri kendilerine uygun olan böbrekleri kavuşacaktı. Bu, Shapley ve Roth’a 2012’de Nobel Ödülü’nü kazandıran atılımdı. (David Gale 2008’de vefat ettiğinden ödülü alamadı.)
Sonuç olarak
Gale ve Shapley çalışmalarına başladıklarında, çalışmaları teorik ve soyuttu. Kararlı evlilik problemi gibi bir şey ile uğraşmaları çok kişiye anlamsız geliyordu. Ancak sonunda çalışmaları ile sayısız insanın hayatını kurtarmayı başardılar. Aynı zamanda herkesi mutlu eden bir çok eşleşme Gale ve Shapley’nin çalışmaları olmadan mümkün olamazdı.
Kaynaklar ve İleri Okumalar:
- How a matchmaking algorithm saved lives; Kaynak site: Medium. Bağlantı: How a matchmaking algorithm saved lives
- College Admissions and the Stability of Marriage; Bağlantı: http://www.eecs.harvard.edu/
- Monteiro, Tiago & Klimentova, Xenia & Pedroso, Joao Pedro & Viana, Ana. (2021). A comparison of matching algorithms for kidney exchange programs addressing waiting time. Central European Journal of Operations Research. 29. 10.1007/s10100-020-00680-y.
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel