Bir parça kağıdı ikiye katlamak gayet basit. Kağıdın iki kenarı çakışacak şekilde üst üste getirip katladığımızda kağıt ikiye katlanmış olur. Peki aynı mantıkla sadece katlama işlemi yaparak bir parça kare kağıdı üçe nasıl katlarız? Haga teoremi ile bunu yapmanız mümkün.

Kağıt katlama ya da diğer adı ile Origami kağıdın icadından bu yana süregelen bir kağıt sanatıdır. Tarih boyunca dini ritüellerden, sanatsal etkinliklere kadar farklı amaçlar doğrultusunda kullanılan kağıt katlama etkinlikleri bilim insanlarını da etkilemiş ve matematikçilerden, mühendislere, pedagoglardan eğitimcilere kadar farklı alanlarda kullanılmıştır.
Origami, Japonca ori (“katlama”) ve kami (“kağıt”) kelimelerinden gelir. Amaç bir kağıdı bantlamadan, yapıştırmadan veya kesmeden üç boyutlu bir yapı haline getirmektir. Bir origami desenleri kitabını karıştırdığınızda, arka plandaki matematiği fark etmemek çok zordur. Aynı matematik karşınıza origami ile yapılmış bir kağıda açtığınız zaman da çıkacaktır. Bu nedenle de origaminin arkasındaki matematik, birçok çalışma alanında giderek daha önemli bir husus haline geliyor.
Haga Teoremi Nedir?
Antik çağlardan beri insanların uğraşa geldiği ve yakın zamana kadar boşa uğraşıldığının bilinmediği bazı problemler vardır. Bunlardan biri de herhangi bir açıyı üç eş parçaya ayırmaktır. Bir açıyı iki eş parçaya ayırmak çok kolayken bunu üç eş parçaya ayırmak imkansızdır. (Tabi bu işlemleri ancak ölçüsüz cetvel ve pergel kullanarak yaparsak imkansız.) İnsanın aklına olur olmaz acaba kare kağıdı üçe katlamak da böylesine imkansız mı? sorusu geliyor.
Bu soruya cevabı Japonya’dan emekli bir biyoloji profesörü olan Kazuo Haga verdi. Bir biyolog olmasına rağmen, matematiği keşfetmek için origami kullanmak onun tutkusu idi. Sonucunda sadece keşfetmekle kalmadı, ayrıca bu konu ile Origamics: Mathematical Explorations Through Paper Folding isimli bir kitap da yazdı. Bu kitabında yazdığı bir katlama yöntemi Haga Teoremi olarak biliniyor. Haga teoremi ile kare bir kağıttan istediğimiz herhangi bir kesri katlamamız mümkündür.
Kağıt Katlama Adımları
Önce kağıdı ikiye katlayalım. İkiye katlandığı kenarın üzerinde var olan katlama çizgisini belirginleştirelim. Şimdi sol alt köşeyi bu yarım işareti karşılamak için kağıdı katlayın. İlk fark edilecek şey şu anda ortaya çıkan, biri sol üstte, biri sağ üstte ve biri de sol altta, kağıdın kenarından sarkan üç üçgen arasındaki ilginç bir ilişkidir. Bu ilişkiyi açıları işaretleyerek sizler de görebilirsiniz. Oluşan bu üç üçgen dik açılı üçgenlerdir ve açılar birbirinin tamamlayanlarıdır. Bu nedenle de bu üç üçgen birbirine benzerdir. Yani aslında aynı üçgenin farklı biçimleridir. Dolayısıyla kenar uzunlukları da birbiri ile orantılı olacaktır.

Kağıdı üçe katlamak için bu benzer üçgenleri Pisagor teoremi ile birlikte kullanabiliriz. Kare kağıdımızın kenar uzunluğunu 1 olarak alırsak, sol üst üçgenimizin bir kenarı 1/2 uzunluğunda, bir kenarı da bilinmeyen x uzunluğunda olacaktır. Bu durumda hipotenüsümüz de 1-x kadar olmalıdır. Bu noktadan itibaren sol taraftaki üçgende Pisagor teoremini yazarsak x2+(1/2)2=(1-x)2 elde ederiz. Gerekli düzenlemeleri yapıp bu denklemi çözersek de x=3/8 sonucuna ulaşırız.
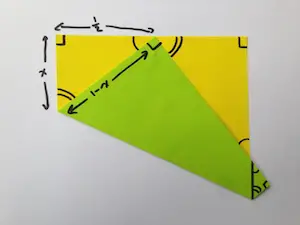
Artık sağ üst üçgenin kenarların uzunluğunu hesaplayabiliriz. Bu üçgenin bir kenarı aşağıda da gördüğünüz gibi y kadar, diğer kenarı da 1/2 kadar olacaktır. Bu aşamadan sonra sol ve sağ üçgen arasındaki benzerlik özelliğini kullanmalıyız. Denklemde x yerine az evvel bulduğumuz x=3/8 sonucunu yerleştirirsek y=2/3 sonucunu elde ederiz.
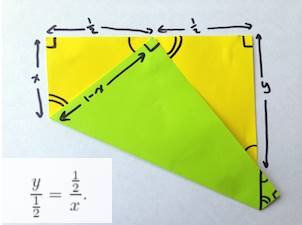
Son durumda y uzunluğunu bildiğimize göre yapmamız gereken tek şey, onun da orta noktasını bulmak olacaktır. Böylece herhangi bir ölçüm yapmadan bir kenarın üçte birini kolayca hesaplamış oluruz.

Kare Kağıdı İstenilen Başka Oranlarda da Katlayabilirsiniz
Başa dönelim. Kağıdın sol alt köşesini üst kenarın yarısına kadar katlamak yerine, sol alt köşeyi üst kenar boyunca herhangi bir noktaya katladığınızı varsayalım. Bu durumda kağıdımız aşağıdaki gibi olacaktır.
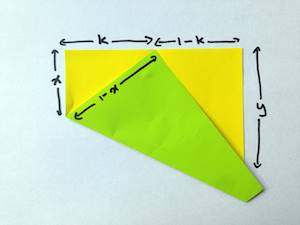
Aslında bu aşamadan sonra yapmanız gerekenler yukarıda anlatılanlar ile aynı. Öncelikle bir kere daha Pisagor teoremi ile işe başlayacağız. x2+k2=(1-x)2 denklemini çözerek x=(1-k2)/2 sonucunu elde etmemiz gerekiyor. Şimdi de bir kere daha sol ve sağ üçgenler arasındaki benzerlik özelliğinden faydalanacağız. Bu durumda da genel bir sonuca ulaşacağız. Bu sonucumuz y/2=k/1+k biçiminde olacaktır. ( Ara basamakları hesaplamayı size bırakıyoruz)
Az evvel k=1/2 olduğunda kağıdımızı üçe katlayabildiğimizi görmüştük. Şimdi k yerine başka değerler vererek kağıdımızı farklı biçimlerde katlayabiliriz. Kağıdımız çevirelim. Üçte birlik noktayı artık bildiğimiz için işe en baştan başladığımızı düşünelim. Bu sayede artık kağıdımızın üzerinde bir kenarın tam olarak dörtte birini işaretleyebiliriz.

Aynı biçimde her kağıt katlama ile yeni bir oran elde edip, ardından kağıdı çevirip, katlama işlemine devam edersek istediğimiz kadar bu işlemi sürdürebiliriz.

Okullarda benzerlik konusunu öğretirken tahtada sıkıcı örnekler çözmek yerine, bir parça kağıt ile hem öğrenmelerini hem de keşfetmelerini sağlamak mümkün. Teşekkürler Haga!
Kaynakça: Folding fractions; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel