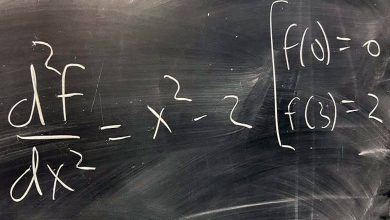Matematik dünyasında kuralları değiştirdiğimiz zaman pek çok ilginç sonuca ulaşmanız mümkündür. Ancak yine de değiştirmemeniz gereken ve bu konuda hepimizin uyarıldığı tek bir kural vardır. Bu kural bize bir sayıyı asla sıfıra bölmememiz gerektiğini söyler. Peki neden tam olarak sıfıra bölmek bu kadar kötü bir fikir?

Normalde bir sayıyı daha küçük sayılara böldüğünüz zaman sonucunuz giderek büyür. Örneğin 20:2=10 iken 20:0,0001 =200.000 olacaktır. Bu durum bize sezgisel olarak böldüğümüz sayı sıfıra yaklaştıkça sonucumuzun da sonsuza yaklaşması gerektiğini düşündürecektir. Bir çok öğrencinin hatalı bir biçimde bir sayıyı sıfıra bölmesi durumunda sonucun sonsuz çıktığını düşünmesi de bununla ilgilidir.
Ancak sonsuza yaklaşmak ile sonsuza eşit olmak çok farklı kavramlardır. Sonsuzluk bir sayı değil, daha ziyade bir fikirdir. Ancak sonsuzu ayrı bir sayı gibi ele alıp bir 1/0 gibi bir kesrin sonucunda eşitlersek matematiksel anormalliklerle karşılaşırız.
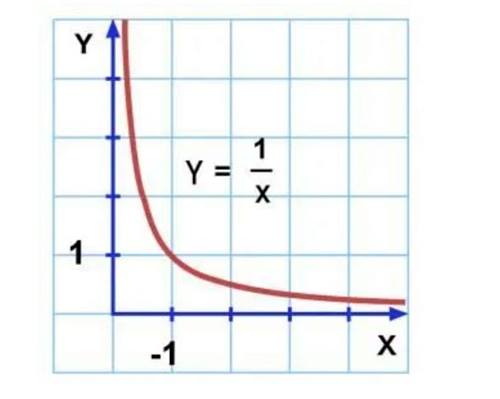
Bölme Nedir?
Aslında sıfıra bölme ile ilgili sorunun neden kaynaklandığını anlamak için öncelikle bölmenin ne olduğunu anlamamız gerekiyor. 100’ün 10’a bölünmesinin sonucu, sonuç 0 olana kadar 100’den 10’u kaç kez çıkarabileceğimizdir. Buradan elde edeceğimiz cevap 10 defa olacaktır. Ancak 20 sayısını sıfıra böldüğünüz zaman sonsuz defa aynı işlemi yapmak zorunda kalırız. Tamam işte cevap yine sonsuz çıktı diye düşünüyorsanız, tam olarak değil.

Matematiğin mevcut kuralları yine matematikçiler tarafından belirlenmiş ve devamında gelenler tarafından da aynı biçimde kabul edilmiştir. Yani genel uyumu bozmadan bu kurallar ile oynamak ve değiştirmek her zaman mümkündür.
Örneğin Euler x2+1=0 denklem sisteminin bir çözümü olmamasından rahatsız olmuştu ve devamında denklemin çözümünden elde ettiği sonuca da hayali sayı ( imaginary) anlamında i demişti. Bu i sayısının tanımıyla ilgili hiçbir sorun yoktu ve mevcut sistem ile uyumluydu. Bu nedenle kabul gördü ve aslında matematikte karşımıza çıkan önemli bir sorunu çözdü.
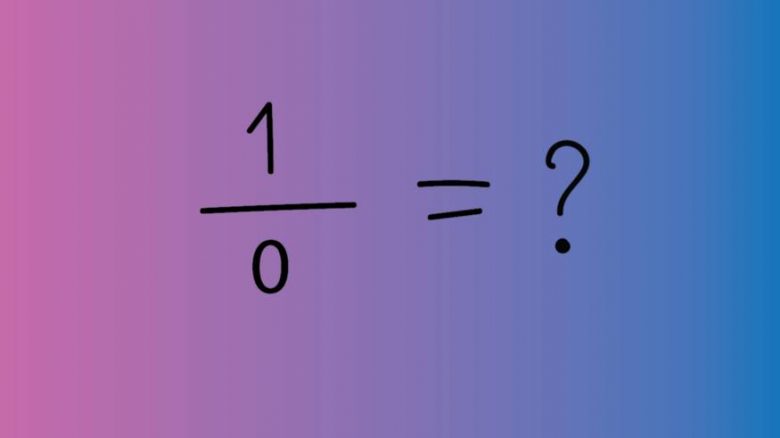
Şimdi sıfıra bölmenin mümkün olduğunu kabul edelim. Hatta bizde Euler gibi düşünelim ve 1/0 ifadesine bir harf atayalım. Diyelim ki Q. Bakalım bu Q matematiğin mevcut sistemleri ile uyumlu mu? Unutmayalım 1/0=Q bu durumda 0 ile neyi çarparsak 1 çıkar sorusunun cevabını Q olarak veriyoruz. Yani Q . 0=1.
Sıfır, herhangi bir sayı veya değişken x için “x – x” olarak tanımlanır. Bu durumda 0 yerine ( 1-1) yazabiliriz. Bu durumda Q.( 1-1)=1 sonucunda ulaşırız. Dağılma özelliğini kullanarak Q-Q=1 yani 0=1 elde ettik. Gördüğünüz gibi Q matematiksel yapıya uymadı yani hata verdi. Bu hatayı ortadan kaldırmak için bazı sınırlandırmalar getirseniz bile karşınıza başka bir hata çıkacaktır. Her durumda baştaki kabulünüz aritmetiğin temel aksiyomları ile uyumsuz olacaktır.
Sıfıra Bölmek Ne Zaman mümkün Olur?
Matematiği öğretme biçimimiz aslında biraz ilginçtir. Bir ilköğretim öğretmeni öğrencilerine küçük sayıdan büyük sayıyı çıkaramayacaklarını söyleyecektir. İlerleyen yıllarda öğrenciler negatif sayılar ile tanışırlar ve bunun mümkün olduğunu anlarlar. Benzer biçimde ilerleyen yıllarda öğretmenler reel sayılarda bir karekökün içinin asla negatif olmayacağını söyler. Ancak karmaşık sayıları öğrendikten sonra öğrenciler bunun da mümkün olduğunu göreceklerdir.

Başlangıçta yasak olarak kabul edilen bir çok kavramın sonrasında olası olduğunu gördüğümüze göre aynı şeyi sıfıra bölmek için de söylememiz mümkün mü? Aslına bakarsanız evet. Eğer sayılar teorisinde çalışmalar yapan bir matematikçiyseniz ve tam olarak ne yaptığınızı biliyorsanız sıfıra bölmek mümkün olacaktır ve oldukça da işinize yarayacaktır. Ancak o vakte kadar sıfıra bölmenin yasak olduğunu kabul etmelisiniz.
Sıfıra bölmenin bir anlamı yoktur çünkü aritmetikte sıfıra bölmek aynı zamanda sıfırla çarpmak olarak da yorumlanabilir. 3/0=X, 0*X=3 ile aynı denklemdir. Bu denklemin doğru olması için X yerine yazılabilecek bir sayı da yoktur.
Sıfırı kendine bölmeye çalışırsanız da benzer bir durum ortaya çıkar. Sıfırı sıfıra bölmeye kalktığımız zaman 0/0=X, 0*X=0 olarak yeniden yazılabilir. Bu durumda da X yerine keyfi herhangi bir sayı yazmak mümkün olacaktır. Bu yüzden de sonuca belirsiz deriz. Yani belli bir cevabı yoktur.
Sıfıra Nasıl Böleceğimizi Bilmek Kalkülüs’ü Mümkün Kılmıştır
Ancak sıfıra bölmenin gerçekten işe yaradığı ve aslında bir sorunu çözmek için gerekli olduğu bazı durumlar da vardır. Aslına bakarsanız Newton Kalkülüs’ün kurallarını bu fikirden yola çıkarak belirlemiştir.
Bildiğiniz gibi Kalkülüs türev, integral ve temelinde eğriler ile ilgilidir. Şimdi bir eğriniz olduğunu ve bu eğrinin belirli bir noktadaki türevini bulmaya çalıştığınızı düşünelim. Bu durumda yapmanız gereken şey eğriye belirli bir noktada teğet çizmek ve o teğetin eğimini bulmaya çalışmaktır.
Ancak çoğu durumda bu eğimi yalnızca cebir kullanarak bulmak imkansızdır. Sıfıra bölme tam da bu noktada işe yarıyor. Oysa ki bu doğruyu teğet değil de eğriyi iki noktada kesecek biçimde çizersek iki noktadan geçen doğrunun eğimini kolayca bulabiliriz.
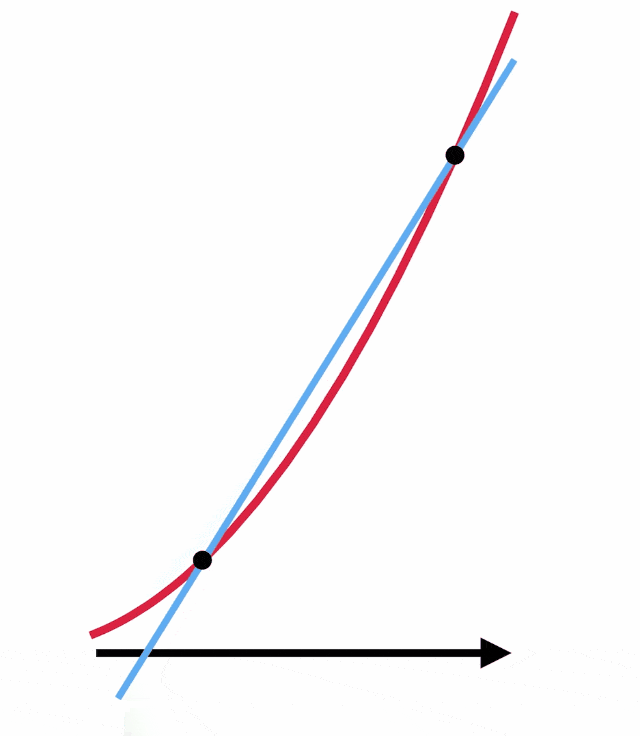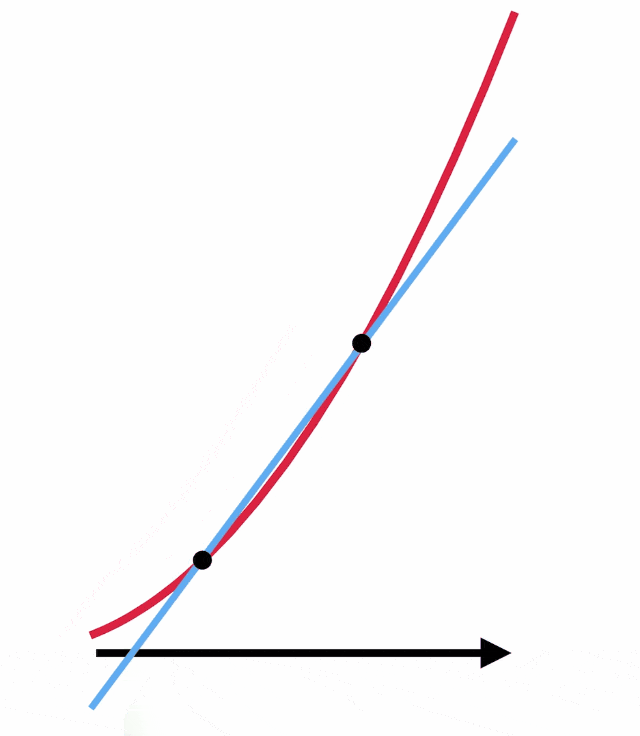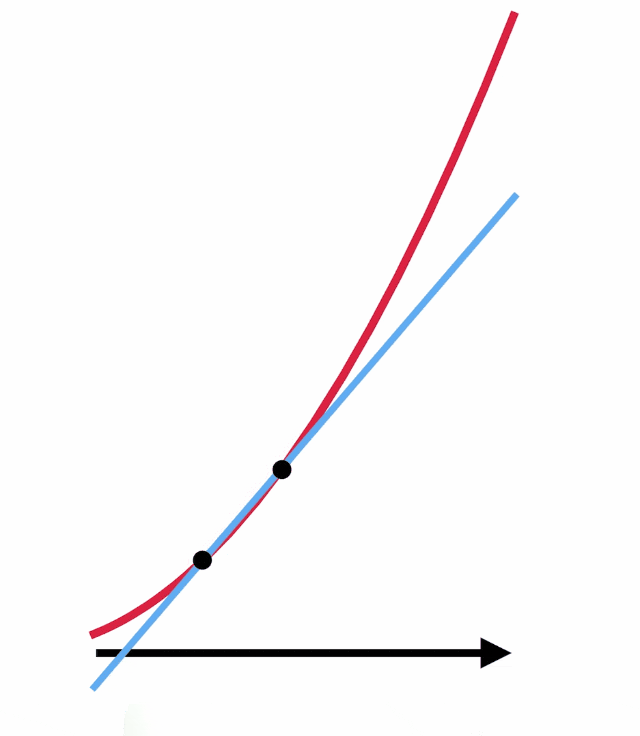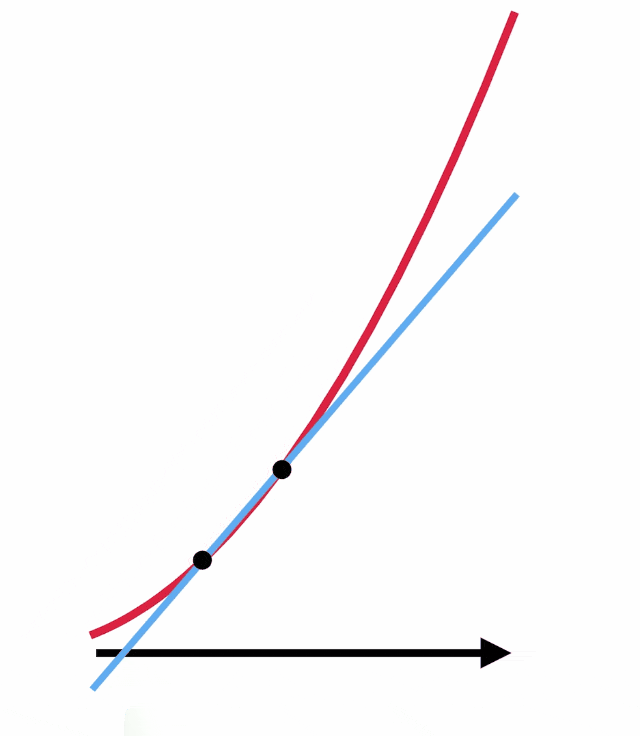
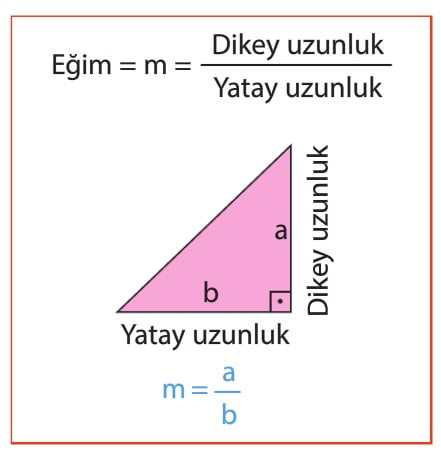
Şimdi bu noktaları birbirine yaklaştırın. Noktalar üst üste çakıştığında bu çizgi aradığınız teğet ile aynı olacaktır. Böylece teğetin eğimini belirlemiş olursunuz. Ancak bu esnada yaptığınız şey aslında sıfır ile sıfırı birbirine bölmektedir. Eğimin tanımı aşağıda gördüğünüz gibidir. Ancak noktaları birbirine yaklaştırdığınız zaman hem dikey hem de yatay uzunluk sıfıra yaklaşacaktır. Ancak 0/0 bölümünden bir sonuç elde etmemiz mümkün olacaktır.
Sonuç olarak
Sıfıra bölmeyi başardığınızda yepyeni bir matematik dünyasının kapıları açılır. Sıfırla, sonsuzluklarla ve her türden imkansız denklemlerle oynamak sıradan hale gelir. Sıfıra bölme sadece tanımsızdır. Bedelini ödemeye hazır olduğunuz zaman onu tanımlamanız olası olacaktır. Sıfır sayısı ile ilgili anlatacak aslında anlatacak çok fazla şey var. Konu ile ilgili bir başka içeriğimize göz atabilirsiniz. Bir Sayının Sıfırıncı Kuvveti Neden Birdir?
Kaynaklar ve ileri okumalar:
- The Secret Magic of Dividing by Zero. Yyaınlanma tarihi: 6 Aralık 2016. Kaynak site: Popular Mechanics. Bağlantı: The Secret Magic of Dividing by Zero
- Problems with Zero – Numberphile; Bağlantı: https://www.youtube.com
- Division by zero; bağlantı: https://en.wikipedia.org/wiki/Division_by_zero
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel