
Hem sonsuzluğu hem de sonluluğu barındıran iki tane matematiksel yapı vardır. Bunlardan bir tanesi Koch kar tanesi ve diğeri ise Cebrail’in borusu olarak isimlendirilir. Bu iki yapının kendine has ilginç bir de özelliği bulunur. Koch kar tanesi olarak isimlendirdiğimiz şeklin çevresi sonsuz iken alanı sonludur. Cebrail’in borusu şeklimizin ise sonsuz bir yüzey alanına ancak sonlu bir hacme sahiptir.
Elbette bu iki şekil ile gerçek hayatta karşılaşmamız olası değildir. Ancak üzerinde iyi çalışılmış bu matematiksel varsayımsal şekiller bilgilerimiz gözden geçirmeye yarayacaktır.
Kock Kar Tanesi Nedir?
Koch kar tanesi genellikle öğrencilerin karşısına çıkan ilk fraktal nesnelerden biridir ve aynı zamanda matematik tarihinde tanımlanan en eski fraktal nesneler arasındadır. Bu karmaşık şekil, ilk olarak İsveçli matematikçi Helge von Koch’un 1904 tarihli “On a Continuous Curve without Tangents, Constructible from Elementary Geometry” başlıklı makalesinde yer almıştır ve bu nedenle günümüzde onun adı ile anılmaktadır.
Ancak bu makaledeki, Koch eğrisi bir eşkenar üçgen yerine bir doğru parçası ile başlar. Daha sonraları matematikçi Robert Fathauer şeklin başlangıcını bir eşkenar üçgen olacak biçimde değiştirmiştir.
Koch kar tanesinin son versiyonunda ilk olarak, bir eşkenar üçgen alırız. Daha sonra bu üçgenin her kenarını üç eşit parçaya ayırırız sonra orta parçasını çıkarıp yerine eşit uzunlukta iki parça koyarız ve bu işlemi sürekli tekrarlarız. Bu oluşumu devam ettirdiğimiz zaman ortaya son derece ilginç bir sonuç çıkacaktır.
Koch Kar Tanesinin Alanı Sonlu Ancak Çevresi Sonsuz Uzunluktadır
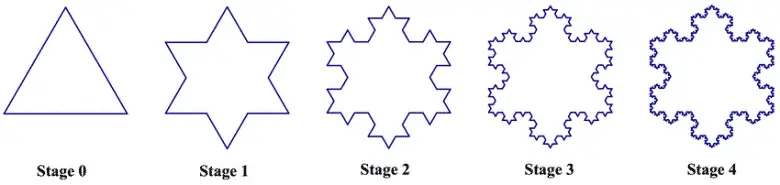
Bizim yapacağımız şey ise bu eğrinin alanını ve çevresini hesaplamak olacak. O zaman alan hesabı ile başlayalım. Bu hesabı yaparken bizim için en önemli olacak şeylerden biri her adımda kaç tane küçük üçgen eklendiğidir. Bir adımda eklenen üçgen sayısı, yukarıda çok rahat görülebileceği şekilde, bir önceki adımın kenar sayısına eşittir.
Başlangıç aşamasını sıfırıncı adım olarak düşünürsek birinci adımdan itibaren her adımdaki kenar sayısı 3.4 n-1 olur. (buradaki n adım sayısını belirtir). Şimdi, başlangıç aşamasındaki eşkenarın üçgeninin bir kenar uzunluğuna x diyelim. O halde, eşkenar üçgenin alanı x2√3/4 olur. Yukarıdaki şeklin alanı içinde şöyle bir toplam elde ederiz:
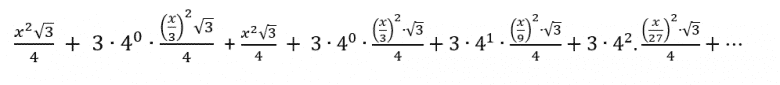
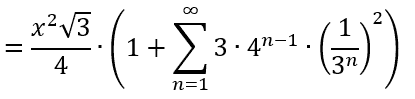
Bu denklemin sağ kısmını biraz düzenlersek lise yıllarından beri gördüğümüz bir geometrik diziyi elde ederiz.
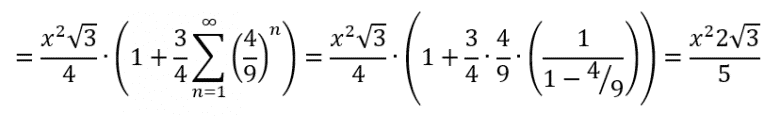
Sonunda alanımızın değerini bulduk. Gördüğünüz gibi alanımız sonludur. Bu değer x’e göre değişen bir reel sayıdır. Şimdi ise çevremizi hesaplamaya çalışalım. Yine başlangıç adımımızdaki eşkenar üçgenin kenar uzunluğunu x alalım.
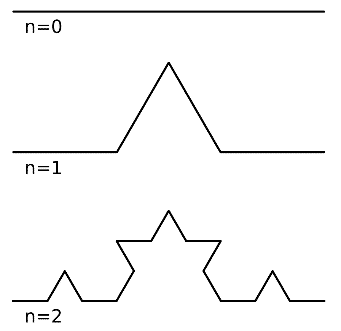
Çevre hesabı yaparken yukarıdaki şekli izlemenin faydası var. Birinci adımda kenarı üç eşit parçaya bölüp bunlardan bir tanesini atıyoruz ve onun yerine iki tanesini ekliyoruz. Sonuçta elimizdeki uzunluk 4x/3 oluyor. İkinci adımda ise bu 4 küçük kenarı yine üçer parçaya bölüyoruz ve aynı işlemi uyguluyoruz ve sonuç olarak elimizdeki şeklin uzunluğu 16x/9 oluyor.
Aynı işlemi yapmaya devam ediyoruz ve tahmin edebileceğiniz gibi n’inci adımda uzunluğumuz x.(4/3)n oluyor. Unutmayalım ki biz bu işleme başlarken sadece bir kenarı baz aldık. Başlangıç adımında elimizde 3 kenar olduğu için her n’inci adımda elimdeki eğrinin çevre uzunluğu 3.x.(4/3)n diyebiliriz.
Şimdiki sorumuz ise şu: Peki biz bu işlemleri sonsuza kadar devam ettirirsek elimizdeki eğrinin çevresi ne olur? Bu soruya liseden hatırladığımız limit konseptini kullanarak cevap verebiliriz. 4/3 sayısı 1’den büyük olduğu için bu limit ıraksar diyebiliriz. Bir diğer deyişle eğrimizin çevre uzunluğu sonsuzdur.
Sonlu Bir Hacme Ancak Sonsuz Yüzey Alanına Sahip Bir Şekil
Şimdi sonsuz bir yüzey alanına ve çok sınırlı bir hacme sahip bir şekli ele alalım. Bu varsayımsal şeklinizin bir kap olduğunu ve onu bir ressama verdiğinizi hayal edin. Ressam, bu şekli kolayca bir kutu boya ağzına kadar başarıyla doldurabilir. Ancak bu ressam, şeklinizin dış yüzeyini boyamaya çalışırsa bunu asla başaramaz. Böyle bir şeklin var olamayacağını düşünüyorsanız yanılıyorsunuz.
Muhtemelen bu yazının başlığından tahmin ettiğiniz gibi, söz konusu geometrik şekil Cebrail’in Borusu Ya da Torricelli’nin Trompeti ( İng: Gabriel’s horn) olarak bilinmektedir. Şekil adını 17. yüzyılda bu şekil ile çalışmalar yapan fizikçi ve matematikçi Evangelista Torricelli’den almıştır. Bu varsayımsal şeklimizi aşağıda görebilirsiniz. Bu şeklin sağ tarafı sonsuza kadar devam etmektedir.
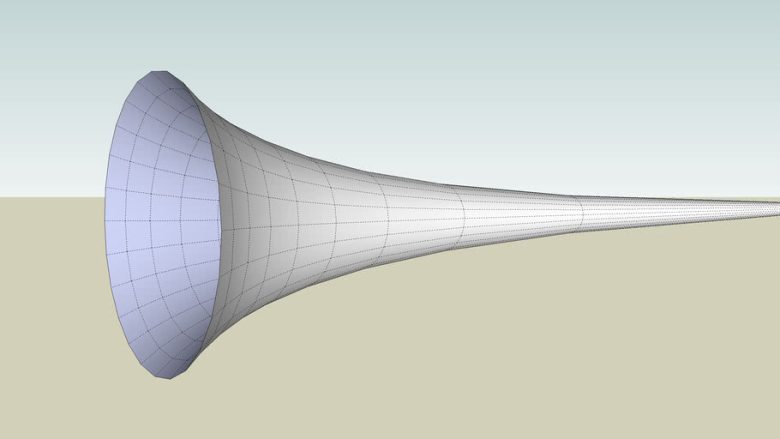
Cebrail’in borusu, y=1/x eğrisinin x’in 1’e eşit ya da büyük olduğu bölgelerde x ekseni etrafında 360 derece döndürülmesiyle oluşmuş bir üç boyutlu şekildir. Hatırlamayanlar için y=1/x şeklinin grafiği aşağıdaki gibi gözükmektedir.
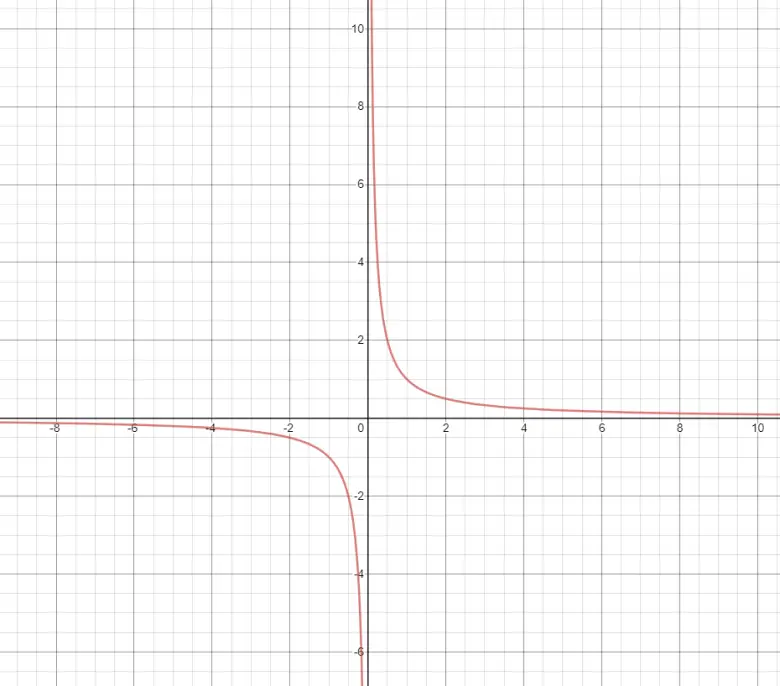
Böyle bir nesnenin gerçekte var olması mümkün değildir. Ancak Torricelli’nin trompetinin sonlu bir hacme, ancak sonsuz yüzey alanına sahip olduğunu göstermek için standart matematik yöntemleri kullanılabilir! Yani bu şekil ancak matematiksel bir dünyada var olabilir.
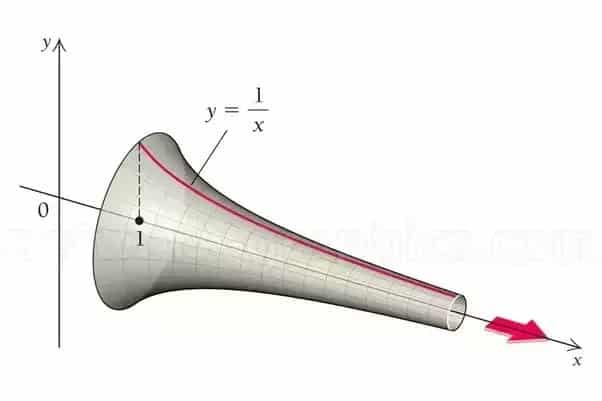
Cebrail’in Borusunun Yüzey Alanı Ve Hacminin Hesaplanması
Önce işe hacmi ile başlayalım. Sınırlı bir hacmi olduğunu bildiğimiz için bunu yapmak daha kolay. İntegralle hacim hesaplama formülünü kullanarak bu hesaplamayı yapabiliriz. Formülü bizim eğrimize uygularsak şunu elde ederiz:
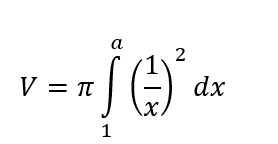
Buradaki a şu anda sadece bir reel sayıyı temsil etmekte olmakla beraber integrali aldıktan sonra bu a’nın sonsuza giderken limitini alacağız. İntegrali alırsak aşağıdakini elde ederiz.
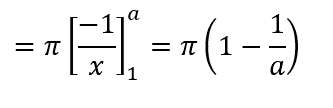
Ve şimdi a sonsuza giderken limit alırsak karşımıza V= π çıkar. Bu da demektir ki Cebrail’in borusunun hacmi sonluymuş. Şimdi de yüzey alanımızı hesaplayalım. Yüzey alanı için uygulayacağımız integral ise biraz daha ileri bir seviye. (Analiz dersi alanların integralle yay uzunluğu bulma kısmından hatırlayacaklardır.)
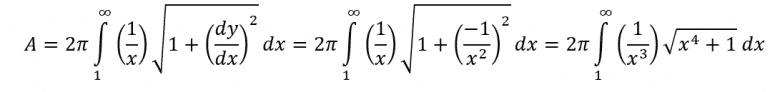
Bu son integralin ıraksak mı yakınsak mı olduğunu anlamamız gerekli.
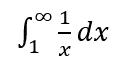
Bunun için onu yukarıda gördüğümüz ıraksak integral ile karşılaştırmamız yeterli. Sonuç, aşağıda gördüğünüz gibi olduğu için bizim integralimiz de ıraksar diyebiliriz.
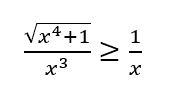
Bu da bize Cebrail’in borusunun yüzey alanın sonsuz olduğunu söyler. Bu yaklaşımlardan yola çıkarak Cebrail’in borusunun içini boya ile doldurabileceğimizi ama onun dış yüzeyini asla boyayamaya yetecek boyaya sahip olamayacağımızı çıkarabiliriz.
Bu içlerinde hem sonsuzluğu hem de sonluluğu içeren ilginç objeler, bilimlerin kraliçesinin sahip olduğu sıra dışı objelerden sadece iki tanesi. Aslında bu gibi matematiksel şekillerden daha çok vardır. Diğerlerini de tanımak içinse tek gereken şey biraz ilgi ve biraz merak…
Kaynaklar ve ileri okumalar:
- Torricelli’s Trumpet & the Painter’s Paradox; Bağlantı: https://onlyphysics.org/
- Torricelli’s Trumpet (or Gabriel’s Horn): A Paradox of Area and Volume; Bağlantı: https://www.youtube.com
- Koch Snowflake; Bağlantı: https://mathworld.wolfram.com/KochSnowflake.html
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










