Geometri dediğimiz zaman aklımıza ilk olarak kareler, üçgenler ve benzer şekiller gelir. Şimdi öğrendiğiniz bu şekiller ile etrafınızda gördüğünüz gerçek dünyayı çizmeye çalışın. Muhtemelen elde edeceğiniz çizim gözünüze fazla da gerçekçi görünmeyecektir. Dünyamız ile Öklid geometrisine uyumlu değildir. Ancak fraktal geometri bu nokta da isinize yarayacaktır.

Fraktal Geometri Nedir?
Fraktal geometrinin ne olduğunu anlamak istiyorsanız bir sonraki denk geldiğinizde bir eğreltiotunu inceleyin. Bir eğrelti otu çoğunlukla daha küçük ölçeklerde defalarca tekrarlanan aynı temel şekilden oluşur. Hepsinden daha şaşırtıcı olanı, bu eğreltiotu yaprağı ne bir ne de iki boyutlu bir şekildir. Aslında ikisinin arasında gezinen kesirli bir boyuttur.
Fraktal geometri adı matematikçi Benoit Mandelbrot tarafından verilmiştir. Kendisi girintili, çıkıntılı şekilleri Latince fraktus yani düzensiz veya parçalanmış kelimesine benzeterek bu ismi kullanmıştır. Ancak o da temelinde kendisinden önceki matematikçilerin çalışmalarını temel almıştır.
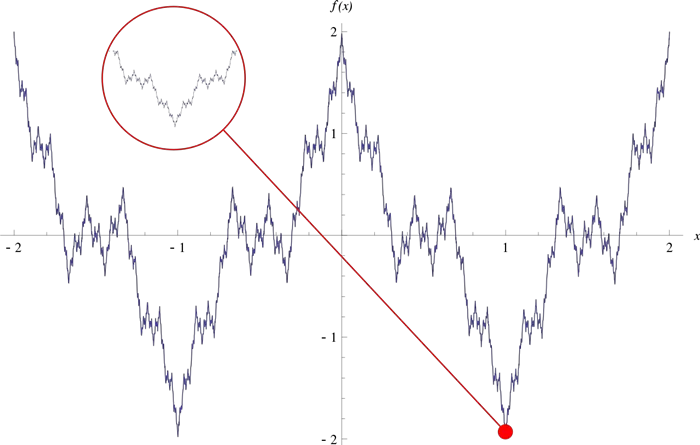
Örneğin 1872’de Alman matematikçi Karl Weierstrass, sürekli fonksiyonlar kavramını tanımlamış ve kendi adıyla anılan, grafiğini aşağıda çizdiğimiz fonksiyonu oluşturmuştu. 1883’te Georg Cantor da matematikçileri rahatsız eden bir başka geometrik şekil ortaya atmıştı. (Bakınız: Cantor set )
Ona ilham veren bir başka kişide Lewis Fry Richardson’dır. Kendisi, 20. yüzyılın başlarında İngiliz kıyı şeridinin uzunluğunu inceleyen bir İngiliz matematikçiydi. Ancak daha sonraları bir kıyı şeridinin uzunluğunun herhangi bir ölçüm aleti ile hesaplanamayacağını dile getirmişti.
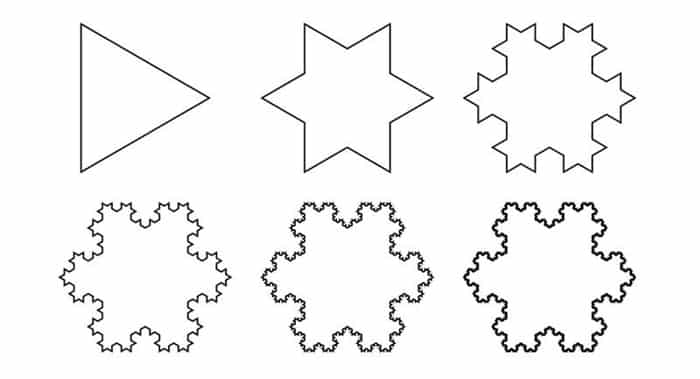
1904’te İsveçli matematikçi Helge von Koch, Koch eğrisi veya “Koch kar tanesi” olarak bilinen aşağıdaki şekil ile konuya dahil oldu. Bunu 1916’da Polonyalı matematikçi Waclaw Sierpinski tarafından oluşturulan Sierpinski üçgeni izledi.
Koch kar taneciği ve Sierpinski üçgeni
Koch kar taneciği şeklini elde etmek için bir eşkenar üçgen alınır. Her kenarı üç eşit aralıkla işaretlenir ve ortadaki bölümler çıkartılır. Buralara kenarları çıkartılan parçalar kadar olan yeni eşkenar üçgenler konur. Bu durumda yeni şeklimizin çevre uzunluğu öncekinin 4/3 katı olmuştur. Bu şekilde her yeni adımda, bir önceki adımda elde edilen doğru parçalarına aynı işlem uygulanınca sonuçta fraktal bir şekil ortaya çıkar.
Koch eğrisinde iki nokta arasındaki uzaklık sonsuzdur. Eğer bu eğriyi yakından incelerseniz şeklin tamamı ile onu oluşturan alt parçaların birbirine benzer olduğu görülür. Örneğin şeklin tamamını 3 kat küçültürseniz bir alt parçasını elde edersiniz.
Bu küçültme işlemine sonsuza kadar devam edebilirsiniz. Koch kar taneciği düzenli denilen, yani çizim kuralları belli olan, fraktallara bir örnektir.
Bu düzenli fraktalların ortak özellikleri, eğrinin bir bölümünü ne kadar büyütürseniz büyütün eğri tam olarak aynı şekli sürdürmeye devam etmektedir. Koch eğrisinin ilginç bir özelliği alanının sonlu olmasıdır, çünkü onu bir daire içine sığdırmak mümkündür. Bununla birlikte her adımda uzunluğu biraz daha artar. Yani alanı sonlu ama çevresi sonsuzdur! Daha fazlası için: Hem Sonlu Hem de Sonsuz Şekiller: Koch Kar Tanesi ve Cebrail’in Borusu

Tanımına göre nokta-0 boyutlu, doğru-1 boyutlu, düzlem-2 boyutlu, küp-3 boyutlu olarak kabul edilir. Peki yukarıda örneğini verdiğimiz geometrik şekiller kaç boyutludur? 1918’de Alman matematikçi Felix Hausdorff bu soruya cevap olarak, kesirli boyutların varlığını önerdi.
Fraktal Şekillerin Boyutları Nasıl Hesaplanır?
Örneğin, Koch eğrisi iki nokta arasında sonsuz uzunlukta olması nedeniyle basit bir doğrunun ötesine taşmakta, diğer taraftan bir düzlemi de tam olarak dolduramamaktadır. Öyleyse Koch eğrisinin boyutu 1 ile 2 tam sayıları arasında yani kesirli bir sayı olmalıdır. Aslına bakarsanız, Koch eğrisinin boyutu 1.26’dır.
İlk bakışta kesirli boyut fikri şaşırtıcı gelse de aslında arka planındaki düşünce biçimi oldukça basittir. Sonucunda bir çizginin ölçeğini üç kat büyütürsek boyu üç kat uzamış olur. 31= 3 olduğundan çizginin boyutu birdir.
Eğer bir karenin ölçeğini üç kat büyütürsek alanı 9, bir başka deyişle 32 kat artmış olur, dolayısıyla boyutu ikidir. Eğer bir küpün ölçeğini üç kat büyütürsek hacmi 33 yani 27 kat artmış olur, dolayısıyla boyutu üçtür. Koch eğrisinde aynı hesabı yaptığımızda, ölçeği üç kat büyütünce kendisi 4 kat büyüyor. Boyutuna D dersek 4 =3D olması lazım. Bunu şöyle de yazabiliriz: D = log34 ve hesapladığımızda karşımıza D= 1,262 çıkar.
Fraktal boyut kavramı ikiden daha büyük değerlere de uzatılabilir. Örneğin düz bir alüminyum folyo 2 boyutludur ancak onu buruşturursanız iki artı bir şey boyutunda bir fraktala dönüştürürsünüz. Bu yeni boyutun kesin değeri folyonun ne kadar kırışık olduğuna bağlıdır ve fraktal kar taneciği için kullanılan yöntemle yaklaşık olarak hesaplayabiliriz. Aradaki tek fark, cetvelle uzunluk ölçmek yerine bu sefer sürekli küçülen ölçü plakaları ile alan ölçüyor olmamızdır.
Dinamik Sistemler ve Fraktallar

İlerleyen süreçte Fransız matematikçi Henri Poincaré, dinamik sistemlerin (zaman içinde değişen sistemler) aynı zamanda kendine benzerliğin fraktal özelliklerine sahip olduğunu buldu. Bu da konuya farklı bir bakış açısı ile yaklaşmamıza neden oldu. Dinamik sistemleri aslında bizler daha çok kelebek etkisi terimi ile tanıyoruz.
Doğaları gereği, bu tarz sistemlerde başlangıç koşullarında oluşan küçük bir değişiklik nihai durumda büyük farkların ortaya çıkmasına neden olabilir. Poincare tarafından teorisini kanıtlamak için geliştirilen diferansiyel denklemler, fraktal yapılara çok benzer şekilde kendi kendine benzerliğe sahip dinamik durumların varlığını ortaya koydu.
1918’de, Poincaré’nin eski bir öğrencisi olan Fransız matematikçi Gaston Julia, kendine benzerlik kavramını araştırmaya başladı. Bu sırada benzer araştırmaları George Fatou’da yapmaya başlamıştı. Sonuçta o sırada çalışmaları fazla ilgi görmese de ikili aslında günümüzde Julia kümesi olarak bilinecek kavramı bulmuşlardı.
Julia Kümesi Nedir?
Bir fonksiyonun Julia kümesi, o fonksiyonun dinamiğini incelemek için kullanılan kümedir. Karmaşık fonksiyonlar, karmaşık düzlemi kendi dinamiklerine göre iki ayrık kümeye bölerler. Bu kümeler, Julia ve Fatou kümeleridir. Fonksiyon, Julia kümesi üzerinde kaotik davranış sergilerken, Fatou kümesinde normal davranış sergiler. Bunun bir örneğini aşağıda görebilirsiniz.

Mandelbrot Kümesi
1970’lerin sonlarında Benoit Mandelbrot “fraktal” terimini ilk kez kullandı. Mandelbrot, IBM’de çalışırken Julia ve Fatou’nun çalışmalarıyla ilgilenmeye başlamıştı. IBM’de bulunan bilgisayar olanaklarıyla, Julia kümesini ayrıntılı bir şekilde analiz edebildi.
Devamında bu küme üzerinde bazı değişkenler ile oynayarak kendi kümesini inşa etti. Bu kümeye yakında bakmak isterseniz verdiğimiz bağlantıdaki animasyona göz atmalısınız. Zooming into the Mandelbrot set

Mandelbröt fraktalları mikroskop altına alırken, İngiliz matematikçi Michael Barnsley aynı nesnelere farklı bir açıdan yaklaşıyordu. Barnsley’in 1988 tarihli kitabı Fractals Everywhere bilgisayarların bilinen eşlemelerinden herhangi bir fraktal şekli hızlı bir şekilde oluşturmasına izin veren bir algoritma içeriyordu. Onun bu çalışması Kaos teorisinin merkezinde yer alan çekiciler ile tanışmamızı sağlayacaktı.
Barnsley ayrıca istenen herhangi bir şekli almanın ve fraktal eşlemeler listesini hesaplamanın bir yolunu da bulmuştu. Aşağıda gördüğünüz eğrelti otu bu sayede çizildi.
Sonuç olarak Fraktal geometri, matematikçilerin gerçek dünyanın düzensizliğini tanımlamasına izin verdi. Dağlar, nehirler, kıyı şeritleri, bulutlar, hava sistemleri, kan dolaşım sistemleri ve hatta karnabaharlar dahil olmak üzere birçok doğal nesne kendine benzerlik gösterir.

Fraktal Geometri İçinde Yaşadığımız Kaotik Dünyayı Anlamanın Bir Yoludur
Fraktal geometri nedir diye sorduk, yazımıza eğrelti otu ile başladık ve eğrelti otu ile tamamlayalım. Sonucunda sizin de gördüğünüz gibi fraktallar, mütevazi bir eğrelti otundan evrenin en büyük ölçeğindeki yapısına kadar çevrenizdeki dünyanın her yerinde bulunmaktadır. Beyniniz de dahil olmak üzere anatominizin belirli kısımları bile fraktaldır.

Bu tarz fenomenleri fraktal geometri kullanarak modellemek, onların davranışlarını ve değişimlerini daha iyi anlamamızı sağlar. Fraktal geometri sadece doğanın şekillerini modellemeye başlamamıza izin vermez, aynı zamanda çevremizdeki dünyaya karşı çocuksu merakımızı yeniden uyandıracaktır.
Kaynaklar ve İleri Okumalar:
- The freaky world of never-ending fractals; https://www.bbc.co.uk/
- Julia kümesi; https://tr.wikipedia.org/
- Explainer: what are fractals?. Yayınlanma tarihi: 11 Aralık 2020; Bağlantı: https://theconversation.com/
Matematiksel










