Güven, ama doğrula. Bu ifade, başkalarına güvenme ile bir durumu kontrol altında tutma isteği arasındaki gerilimi ifade eder. Matematikçi Adi Shamir, kendisiyle anılan “Shamir’in sır paylaşımı” algoritmasını geliştirdiğinde muhtemelen bu zorluğu düşünüyordu.

Bu algoritmayı anlamak için, öncelikle bir bulmaca üzerinde düşünelim. Diyelim ki yaşlı bir kadın, bir şifreli kilitle korunan kasasındaki değerli eşyaları beş oğluna miras bırakmak istiyor. Ancak, her birinden şüpheleniyor. Kodun sadece birine verilmesi halinde, onun kasanın içeriğiyle kaçmasından korkuyor. Bu nedenle, her bir oğluna bir ipucu vermek istiyor, ancak yalnızca beşi bir araya gelirse kasa açılabilmeli. Kadın bu durumda ne yapmalı?
Görev basit gibi gelecektir. Örneğin, eğer kasanın kilidi beş basamaklı bir şifre gerektiriyorsa, her oğluna bir rakam vererek birlikte kasayı açmalarını sağlamak olasıdır. Ancak bu senaryoda, eğer üç oğul iş birliği yaparsa, diğer iki kardeşi devre dışı bırakabilirler. Üç müttefik, şifrenin yalnızca iki rakamını bilmiyor olacaktır ve bu iki eksik rakamı deneme-yanılma yoluyla hızlıca tamamlayarak kasayı açabilirler.
Bu nedenle, kadın, yalnızca beşinin birlikte çalışması durumunda kullanılabilecek bir şekilde bilgiyi dağıtmak istiyor. Eğer beş kişiden ikisi, üçü veya dördü bir araya gelirse, ellerindeki bilgiler işe yaramaz olmalı. Bu gereklilik, görevi çok daha karmaşık hale getiriyor.

Ancak 1979 yılında, bu zorluk Adi Shamir’i caydırmadı. Kendisinin bulduğu yöntem gerçekten sıradışı idi. Ancak matematikçi Adi Shamir’in, Ron Rivest ve Leonard Adleman ile birlikte “RSA algoritması” olarak adlandırılan algoritmayı geliştiren kişi olduğunu düşününce sonuç çok da şaşırtıcı değil.
Shamir’in Sır Paylaşımı Algoritması Nedir?
Shamir’in Sır Paylaşımı Algoritması, modern kriptografide ve veri güvenliğinde devrim niteliğinde bir yöntemdir. Kritik bilgilerin güvenli bir şekilde saklanması ve paylaşılmasında sunduğu matematiksel kesinlik ve esneklik, onu hem teorik hem de pratik açıdan önemli bir araç haline getirir. Bu algoritma, özellikle güvenliğin en üst düzeyde tutulması gereken durumlarda, bilgilerin kaybolmasını veya çalınmasını önlemek için güçlü bir çözüm sunar.
Shamir’in sır paylaşma yöntemini anlamak için somut bir sayısal örneğe bakmak faydalı olacaktır. Diyelim ki kadının şifresi 43953 ve sadece iki oğlu var. Eğer bir oğluna “439”u, diğerine ise “953”ü söylerse, ikisine de aynı miktarda bilgi vermiş olur. Bu durumda çocukların her biri eksik olan iki rakamı tahmin etmeye çalışır ve birlikte çalışmaya gereksinim duymazlar. Onların birlikte çalışmalarını sağlamak için olaya farklı bir pencereden bakmamız gerekecektir.
Herkesin bildiği gibi iki noktadan bir doğru geçer. Bir tek noktadan da sonsuz sayıda doğru geçer. Yani bir doğru için birlikte çalışmak gereklidir. Diyelim ki kadın kafasında y = 5x + 43953 denklemini belirledi. Büyük oğluna P1 noktasının koordinatlarını (33503, 211468) verdi. Diğer oğluna da P2 noktasının koordinatlarını (85395, 470928) verdi.
Çocukları matematikte kötü olsalar bile kasanın şifresini artık kolayca belirleyebilirler. Bunun için iki noktanın koordinat düzleminde yerini bulup, noktaları işaretleyip, bir cetvel ile birleştirebilirler. Bu doğrunun y ekseniyle kesiştiği nokta aradıkları şifre olacaktır.
Ya Kadının Daha Fazla Çocuğu Varsa?
Kadının iki değil üç çocuğu varsa da aynı yöntem izlenebilir. Ancak bu durumda kadının şifreyi gizlemek için düz bir çizgiyi değil, bir parabolü seçmesi gerekecektir. Diyelim ki kadın y = 5x2 + 10x + 43953 fonksiyonunu seçip oğullarının her birine parabol üzerinde bir nokta vermiş olsun. Bu denklemin de y ekseniyle kesişme noktası istenen çözüme yani 43953 sayısına karşılık gelecektir.
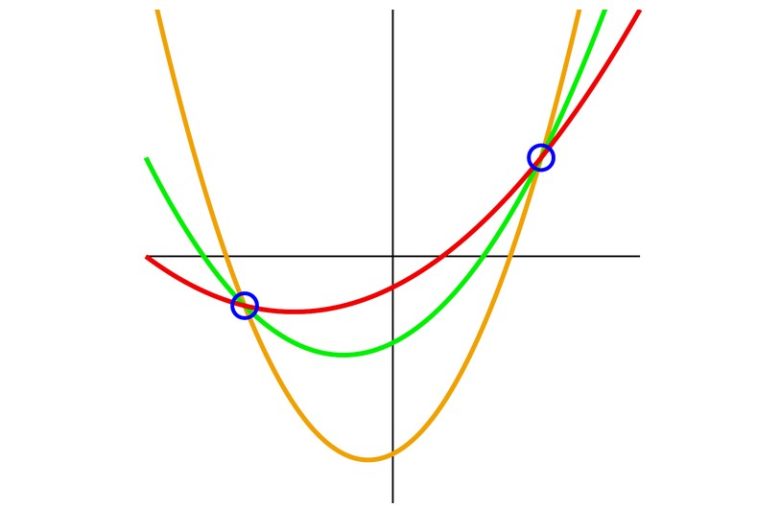
Ancak bu durumda da çocuklardan ikisi birleşip üçüncüye karşı komplo kuramaz. Çünkü iki noktadan da sonsuz sayıda parabol geçer. Bu durumda y ekseni ile kesişme noktasını ve dolayısıyla kasanın şifresini bulmak için üçüncü kardeşin yardımı yine gerekecektir.
Aynı mantıkla devam edersek, dört oğlu olan bir kadın, y = ax3 + bx2 + cx + 43953 türünde bir denklem ile şifreyi saklayacaktır. Beş oğlu olan bir kadın da dördüncü dereceden bir polinom denklemi kullanır (örneğin, y = ax4 + bx3 + cx2 + dx + 43953) vb.
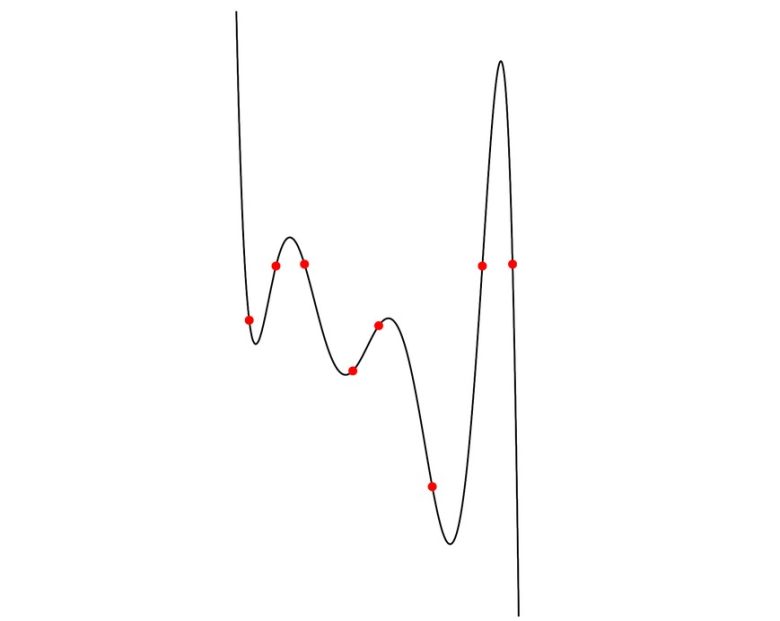
Ama bir sorun var. Beş çocukla ilgili senaryoya geri dönelim. Eğer dördü bir araya gelip, diğer kardeşe komplo kurarsa, dört noktayı kullanarak dördüncü derece denklemi basitleştirebilirler. Şifreyi tam olarak bulamasalar da sonunda iki bilinmeyenli bir denklemle karşı karşıya kalırlar.
Bu denklemde bilinmeyen olarak a parametresi ve c yani aradığımız şifre vardır. Ayrıca bu çocuklar c’nin yani şifrenin pozitif bir tamsayı olduğunu biliyorlar. Ayrıca kadının yaşı vb gibi unsurları dikkate alarak a parametresinin de pozitif tamsayı olması gerektiğini varsayabilirler.
Bu da olasılık aralığını önemli ölçüde kısıtlamaktadır. Kardeşler farklı çözümleri denemek için bir bilgisayar programı kullanırsa kısa sürede şifreyi bulacaklardır. Böyle bir senaryodan kaçınmak için Shamir’in başka bir fikri vardı. Gerçek sayılarla hesaplama yapmak yerine daha küçük bir sayı sistemi ile çalışmaya karar verdi. Bu sayı sisteminde de dört işlem yapabiliyordu.
Shamir’in Sır Paylaşımı Güvenliği Nasıl Sağlar?

Shamir’in algoritması, matematiksel olarak Lagrange interpolasyonu ve modüler aritmetik üzerine kuruludur. Algoritmanın temel çalışma prensibi şu şekildedir:
- Elinizde paylaşmak istediğiniz bir sır (örneğin, S) vardır. Bu sır genellikle bir sayı veya dizi olarak temsil edilir.
- Rastgele bir dereceli bir polinom oluşturulur. Bu polinomun sabit terimi sırrı temsil eder: P(0)=S
- Polinomun, belirli değerlerdeki sonuçları (örneğin, x1,x2,…,xn) hesaplanır. Her bir (x,P(x))çifti, sırdan bir parçayı temsil eder ve bu parçalar farklı paydaşlara dağıtılır.
- En az k sayıda parça bir araya getirildiğinde de, polinomun katsayıları Lagrange interpolasyonu kullanılarak yeniden hesaplanabilir. Bu işlem sonucunda polinomun sabit terimi, yani sır, ortaya çıkar. Eğer k sayısından daha az parça bir araya getirilirse, sır yeniden oluşturulamaz. Bu özellik, algoritmanın güvenliğini artırır.
Sır olarak S=1234 seçilsin. Paylaşımları oluşturmak için ise P(x)=1234+567x+890x2 polinomunu oluşturalım. Burada 1234 sırdır ve 567 ile 890 rastgele katsayılardır. Paydaşlara verilecek paylaşımlar, polinomun belirli x değerleri için hesaplanır.
- x=1 için P(1)=1234+567⋅1+890⋅12=2691 ise birinci kişinin sırrı (1,2691)
- x=2 için P(2)=1234+567⋅2+890⋅22=5182 ise ikinci kişinin sırrı (2 ,5182)
- x=3 için P(3)=1234+567⋅3+890⋅32=8175 ise üçüncü kişinin sırrı (3, 8175) biçiminde olacaktır. Sırrı yeniden elde etmek için de en az k=3 gerekir ve buradan da polinom Lagrange interpolasyonu aracılığı ile yeniden elde edilir.
Sonuç olarak
Yaşlı kadın bu hesaplama ile kardeşlerin birbirlerine karşı komplo kurmaları neredeyse imkansız hale getirecektir. Tek çare kardeşlerin şifreyi bulmak için birlikte çalışmalarıdır.
Günümüzde Shamir’in Sır Paylaşımı algoritması, özel bilgilerin (“sırların”) güvenilmeyen bir ağ üzerinde, güvenli bir şekilde dağıtılmasına olanak sağlayan önemli bir şifreleme algoritması olarak varlığını sürdürmektedir. Shamir’in algoritması, blokzincir teknolojilerinde çoklu imza protokollerinde veya akıllı sözleşmelerde de kullanılmaktadır.
Kaynaklar ve ileri okumalar
- Shamir, A. (1979) How to Share a Secret. Communications of the ACM, 22, 612-613.
http://dx.doi.org/10.1145/359168.359176 - How Cryptographic ‘Secret Sharing’ Can Keep Information Safe. Yayınlanma tarihi: 7 Aralık 2023. Kaynak site: Scientific american.Bağlantı: How Cryptographic ‘Secret Sharing’ Can Keep Information Safe
Matematiksel