Domain coloring – Tanım kümesi renklendirme, karmaşık değerli fonksiyonların grafiklerinin anlaşılmasını kolaylaştıran bir yöntemdir. Bu yazıda bu yöntemi nasıl uygulayabileceğimizi anlamaya çalışalım.

Fonksiyonların grafiklerini çizmeyi hepimiz az çok biliriz. Örneğin bir f(x)=x2 fonksiyonunun grafiğinin, bir parabol şeklinde olacağına veya f(x)=sin(x) fonksiyonunun grafiğinin, periyodik bir biçimde çizileceğine zaten aşinayız. Fonksiyonun grafiğini çizerken bildiğiniz gibi, fonksiyonu tanımsız yapmayan herhangi bir girdisini yazdıktan sonra y eksenindeki değerini buluruz. Sonrasında da kesişim yerlerini belirleriz. Sırayla birkaç girdi hesapladıktan sonra, fonksiyonun grafiği kabaca ortaya çıkar.
Tabi ki bu anlattıklarımız tek değişkenli fonksiyonlar için geçerlidir. Çok değişkenli fonksiyonların grafiğini çizmek boyut sayısı artacağı için işler bir hayli zorlaşır. Örneğin f(x,y)=x.y fonksiyonunun grafiğini çizerken 2 girdi 1 çıktı sayısı olduğundan toplamda 3 boyutta grafiğini kolayca gösterme mümkündür.
Domain Coloring – Tanım Kümesi Renklendirme Nedir?
Peki sizce bir f(z)=z karmaşık değerli fonksiyonun grafiğini nasıl görselleştirebiliriz? Bu fonksiyonda 2 girdi 2 çıktı (f(x+iy)=x+iy) olacağından ve bu fonksiyonu 4 boyutta temsil etme şansımız pek mümkün olamayacağından farklı bir teknik uygulamak gerekir.
Aslında ‘Riemann Yüzeyi’ gibi karmaşık değerli fonksiyonları görselleştirecek başka teknikler de vardır. Fakat şu anda, tanım kümesi renklendirme biçiminde Türkçe’ye çevirebileceğimiz Domain Coloring yöntemine odaklanacağız. Bu yöntem 1980’li yıllarda Larry Crone ve Hans Lundmark adlı iki matematikçi tarafından geliştirildi. 1988 yılında ”Domain Coloring” terimini literatüre kazandıran kişi ise Frank Farris adında bir matematikçi oldu.
Tanım kümesi renklendirme, karmaşık değerli fonksiyonların grafiklerinin anlaşılmasını kolaylaştıran bir yöntemdir. Karmaşık düzlemde her bir noktaya bazı renkler atanır. Düzlemde renkler ile atanan noktalar farklı renklerde ve tonlarla temsil edilir. Bu sayede 4 boyutlu karmaşık fonksiyonların grafikleri 2 boyuta indirgenir. Bu da grafiğin daha kolay anlaşılmasını ve çizilmesini sağlar. Teknik, fizik ve mühendislik alanlarında da kullanım alanlarına sahiptir.
Tanım Kümesi Renklendirme Örnekleri
Aşağıda f(z)=z fonksiyonunun grafiğini görüyorsunuz. Peki hangi karmaşık sayı hangi renk ile temsil edilir?
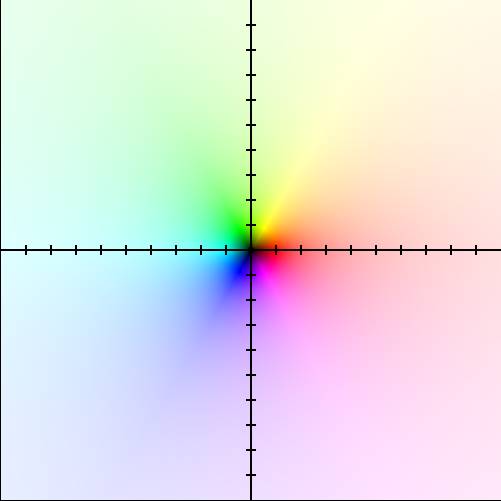
Cevap grafikte size bakıyor gibi. Karmaşık diyagramda sanal ve reel düzlemi biliyorsanız y ekseni ya da ordinat, sanal ekseni x ekseni ya da apsis, reel ekseni temsil etmektedir. Fonksiyon birim fonksiyon olduğu için ve dolayısıyla girdi çıktıya eşit olacağından renklerin hangi tarafı temsil ettiği açıkça bellidir ve bunlar: Kırmızı renk, pozitif reel sayıları, yeşil renk, pozitif sanal sayıları, turkuaz renk negatif reel sayıları ve mor renk negatif sanal sayıları temsil eder.
Renk karışımlarından tahmin ettiğimiz de z karmaşık sayısını x+iy şeklinde tanımlarsak x+iy sayısını kırmızı+yeşilden oluşan sarı renk, x-iy sayısını kırmızı+mor’dan oluşan fuşya renk,-x+iy sayısını turkuaz+yeşil’den oluşan camgöbeği rengi,-x-iy sayısını ise turkuaz+mor’dan oluşan mavi renk temsil eder.
Biraz da siyah ve beyaz renklerden bahsedersek, aslında bahsettiğimiz bu renkler renkten çok rengin tonuyla ilgilidir. Renk ne olursa olsun, tonunu sıfıra çekersek beyaza, yükseltirsek yavaş yavaş siyaha bürünür. Peki bunu Domain Coloring tekniğinde nasıl belirleriz? Başta dediğimiz gibi fonksiyonun sıfırları, grafiğinin x eksenini kestiği noktalardır. Bu noktalar karmaşık düzlemde siyah renk ile temsil edilir. Aşağıda f(z)=z2+1 ve f(z)=z3/100 -1 fonksiyonlarının grafiğini görmektesiniz.
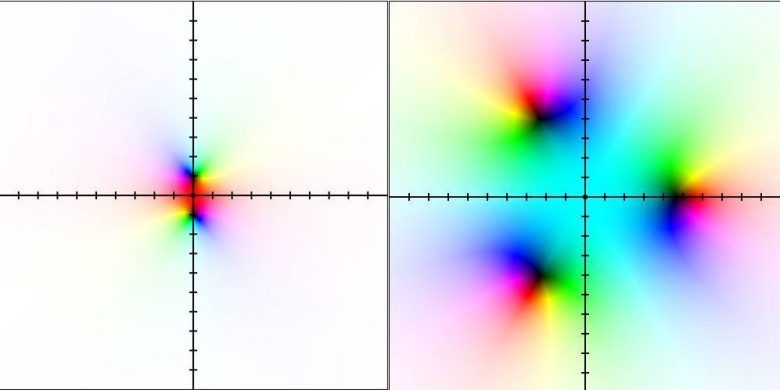
İlk grafikte görüldüğü üzere siyah noktalar i ve -i sayılarının yerlerine yerleşmişlerdir. Çünkü fonksiyon i ve -i noktalarında sıfır olmaktadır. 2.grafikte ise 3. dereceden bir polinom görmekteyiz. Yani bu fonksiyonun grafiğinde çakışık kökler yoksa 3 tane siyah nokta olacaktır. Çakışık kökler olduğunda 2 girdi aynı değeri vereceğinden grafikte tek siyah nokta olur. Şunu da unutmayalım, karmaşık analizde bu siyah noktalara fonksiyonun sıfırları denir. Tamamen beyaz renk senaryolarında ise devreye sonsuzluklar girmektedir. Zaten karmaşık analizde bunlara fonksiyonun kutupları da denir. Aşağıda f(z)=1/z ve f(z)=e1/z fonksiyonlarının grafikleri gösterilmiştir.
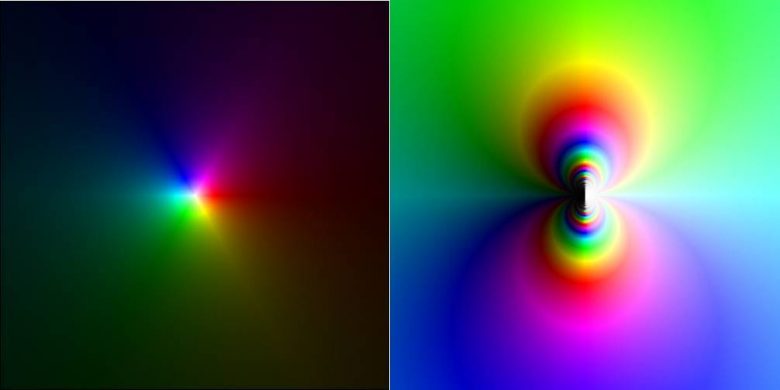
Artık grafiklere aşina olduğunuz için eksenlere gerek duymadık. İlk grafikte orijin noktasının beyaz renkte olduğunu görmekteyiz. Çünkü fonksiyon sıfır noktasında tanımsız olmaktadır. İkinci grafikte ise orijinde esaslı tekillik görmekteyiz. Bir fonksiyon ne kadar sonsuza yaklaşırsa grafiği o kadar çok soluk bir renge bürünür. Aksine fonksiyon ne kadar sıfıra yaklaşırsa da tonlar o kadar canlı olur. Burayı daha iyi anlamak için aşağıdaki grafiklere bakabilirsiniz.

Yalnız yöntemde önemli bir eksik olduğunu fark etmişsinizdir. O eksik tekniğin renk körleri için işlevsiz olmasıdır. Bu sorun kişinin ayırt edebildiği alternatif renk haritaları kullanılarak kısmen de olsa giderilir. Örneğin döteranopi veya kırmızı rengi mavi ve yeşil renklerinden ayırt edememe rahatsızlığından mahrum kişiler mavi/yeşil/kırmızı renk tabanlarını kullanmak yerine mavi/gri/yeşil renk tabanlarını kullanmaları grafiğin anlaşılması için daha da etkili olabilir.
Tamamen pigment eksikliğinde ise sadece siyah ve beyaz renkler ayırt edilebileceğinden sayıların sadece büyüklükleri anlaşılabilir. Yani anopi veya sadece siyah ve beyaz renklerini algılama hastaları için bu yöntem işlevsiz kalır.
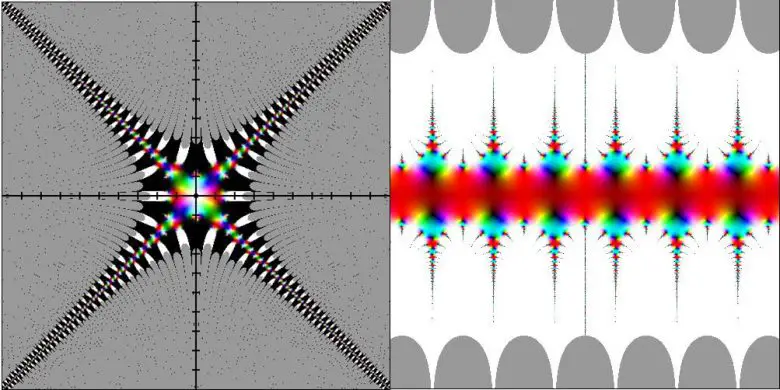
Son olarak 0/0, sonsuz/sonsuz, 0.sonsuz ve sonsuz-sonsuz gibi belirsiz ifadeler ortaya çıktığında siyah ile beyaz’ın karışımından gri renk ile temsil edilir. Aşağıda bunun örnekleri olan f(z)=Γ(sinh(z2) ve f(z)=-sin(cos(sin(z))) fonksiyonlarının grafiğini görmektesiniz.
Konuk Yazar: Feyzi Gök
KAYNAKLAR
- Poelke K, Polthier K. Domain coloring of complex functions: an implementation-oriented introduction. IEEE Comput Graph Appl. 2012 Sep-Oct;32(5):90-7. doi: 10.1109/MCG.2012.100. PMID: 24806991.
- Ponce Campuzano, Juan. (2021). Domain colouring for visualising and exploring the beauty of complex functions. 48. 162-170.
- Visualizing complex-valued functions in the plane; https://www.maa.org/
Matematiksel










