Son iki bin yılda, parabol Arşimet, Galileo ve daha pek çok matematikçi için bir çalışma konusu olmuştur. Çünkü parabollerin birkaç ilginç özelliği vardır. Örneğin bir parabolün grafiği çarpma yapmak ve asal sayıları bulmak için de kullanılabilir.
Bilgisayarlardan önceki zamanlarda; astronomi, navigasyon ve daha pek çok kapsamlı hesaplama gerektiren alanlara yardımcı olmak için çeşitli matematiksel yöntemler icat edildi. Bunların arasında çeşitli amaçlar için kullanılan nomogramlar da vardı.
Nomogramlar, bir matematik formülünün grafiksel gösterimi şeklinde tanımlanır. Bir parabolün grafiği de, iki sayının çarpımına yardımcı olmak için nomogram olarak kullanılabilir. Detaylara geçmeden önce temel bilgileri anımsayalım.
İkinci dereceden y = ax2 + bx + c fonksiyonunun bir grafiği, parabol adı verilen U şeklinde bir eğri oluşturur. Bu ikinci dereceden denklemin gerçek (sanal olmayan) çözümleri mevcut ise bunlar parabolün x eksenini kestiği noktalar olur.
Parabol İle Çarpma İşlemi Nasıl Yapılır?
Parabol x eksenini yalnızca bir kez keserse bu çakışan köklerin olduğu yani iki kökün birbirine eşit olduğu anlamına gelir. Bu durumu temsil eden en basit denklem y=x2 biçimindedir. Şimdi çarpma işlemini nasıl yapabileceğimize bakabiliriz.
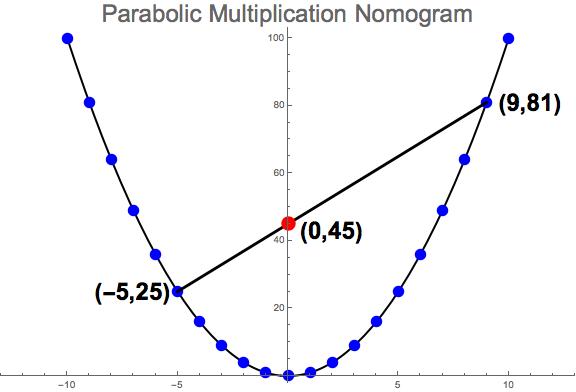
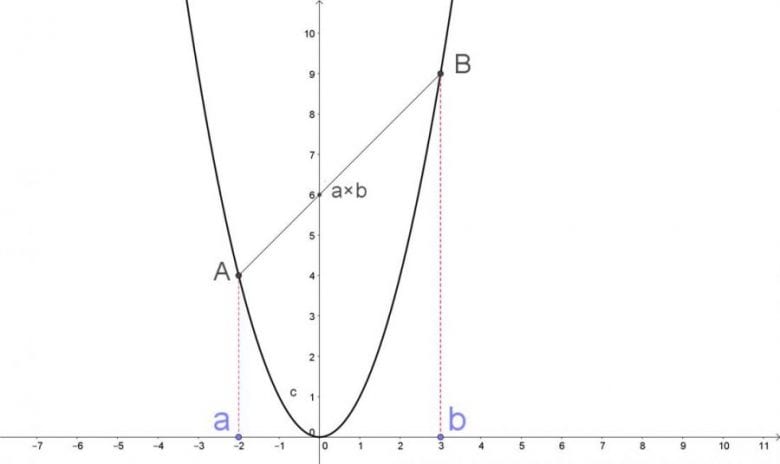
İşe öncelikle y=x² parabolünün grafiğini çizerek başlayalım. Parabol üzerindeki herhangi iki noktayı birbirine bağlamak için yapılması gereken şey aralarında bir çizgi çizmek olacaktır. Diyelim ki x1 ve x2 değerlerini çarpmak istiyoruz.
Şimdi grafikte {(x1,x12)} ve {(x2,x22)} noktalarını işaretleyin. Sonrasında da bu noktaları birleştiren düz bir çizgi çizin. Sonucunu yukarda da göreceğiniz gibi, çizdiğiniz doğrunun y ekseni üzerindeki değer size çarpımı verecektir. ( Sonucun işe yaraması için seçtiğiniz iki nokta y ekseninin iki farklı tarafında olmalıdır.)
İSPAT: y=x2 bir parabol, –a ve b, x ekseni üzerinde alınan noktalar olsun. A=(-a, a2) ve B=(b,b2) sıralı ikililerini kullanarak AB doğrusunun denklemini yazalım. Bunun için iki noktası bilinen doğrunun denklemi formülünden yararlanıyoruz. Burada: x1=b , y1=b2 , x2=-a ve y2=a2 aldığımızı söyleyelim. Bu durumda AB’nin denklemi şu biçimde olacaktır: y-b2=-(a-b)(x-b)
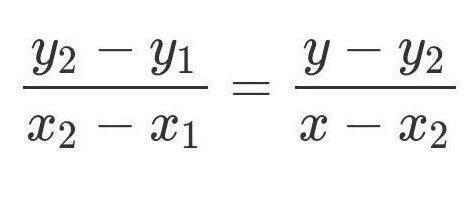
AB ile y ekseninin kesim noktasını bulmak için AB’nin denkleminde x=0 yazmamız gerekiyor. Bu durumda y-b2=-(a-b)(0-b) elde ederiz. Bunu biraz daha düzenlersek, -b2=ab-b2 biçiminde yazılabilir. Sadeleştirmelerden sonra da geriye y=ab kalacaktır. Bu da zaten varmak istediğimiz sonuçtur.
Parabolik nomogramın bir başka uygulaması da iki sayının geometrik ortalamasını bulmaktır. Normalde geometrik ortalama işlemlerinde işin içine karekök karışacaktır. Ancak bir parabol grafiğine bakarak da bunu bulmanız mümkündür. Basit olması için bunu yine y=x2 parabolünde düşünelim. Bu sefer m ve n sayıları için {(0,m)} ve {(0,n)} noktalarından geçen yatay çizgiyi çizin. Bu çizginin y eksenin kestiği nokta aslında aradığınız geometrik ortalamadır.
Parabol İle Asal Sayıları Bulmanız da Mümkündür
Boris Stechkin tarafından tasarlandı.
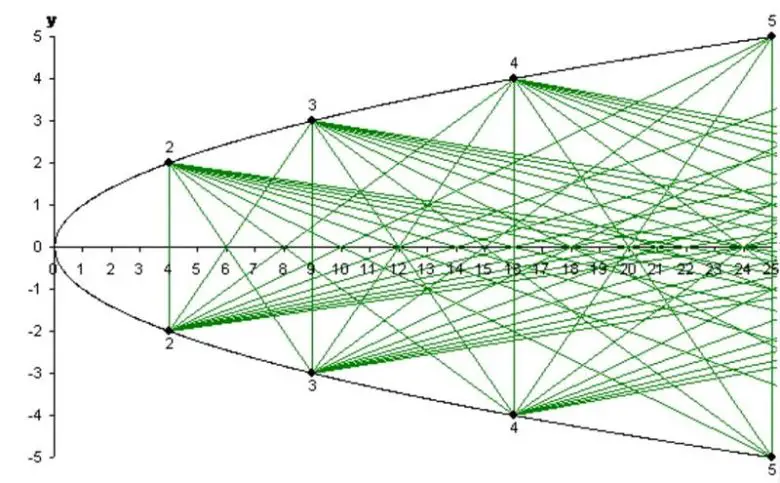
Az önce gördüğümüz teknikle, çarpma yapmayı öğrenmek aslında işin ilk adımı. Aslında parabol ile çarpmaya benzer bir teknikle asal sayıları bulmanız da mümkündür. Yukarıdaki grafik bir parabolün yan dönmüş halidir. Yani aslında x değeri ile y değeri yer değiştirmiştir. Bu geometrik diyagrama, matematikçi Yuri Matiyasevich’in adı verilmiştir ve Matiyasevich’in eleği denir.
Aslında yukarıdaki şekle dikkatli bakarsanız parabol ile asal sayıların ilişkisini kolayca fark edeceksiniz. Gördüğünüz gibi x ekseni üzerinde tüm tamsayılar bulunuyor. Ancak bazılarından çizgi ya da çizgiler geçerken bazıları açıkta kalmış durumda. İşte bu açıkta kalan sayılar asal sayılardır. Şimdi bunun nasıl mümkün olduğunu anlamaya çalışalım.
Parabol İle Asal Sayıları Bulma Aslında Parabol İle Çarpma Sonucudur
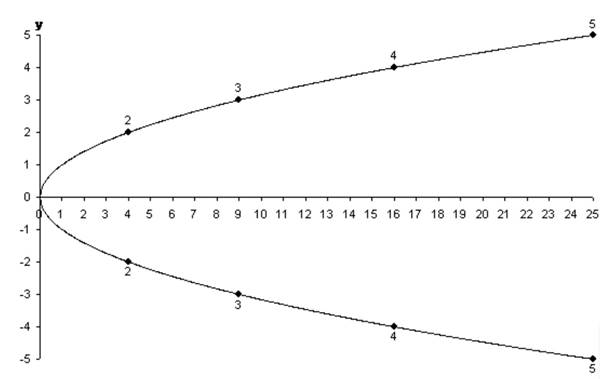
Öncelikle x ve y eksenlerini çiziyoruz. Sonrasında da x=y2 eğrisini çiziyoruz. Gördüğünüz gibi bir parabol elde ettik. Şimdi parabol üzerinde (4,2) noktasını 2; (9,3) noktasını 3; ( 16,4) noktasını 4 olarak işaretleyelim ve bu biçimde devam edelim. 2’den büyük bütün (m2,m) noktaları y ekseninin üst kısmında yer alsın. Sonra y ekseninin alt kısmında da (n2,-n) noktalarını aynı mantıkla işaretleyelim.
Şimdi (4,2) noktasını alalım ve alt kısımdaki tüm noktalar ile düz bir çizgi ile birleştirelim. Sonrasında da aynısını (4, -2) için yapalım. Sonrasında da aynı uygulamayı (9,3) ve (9,-3) ve diğer tüm noktalar için yapalım. Sonuçta parabolünüz aşağıdaki gibi olacaktır. Biz diyagramı oluştururken asal sayıların sırası ise gözlerimizin önünde belirecektir.
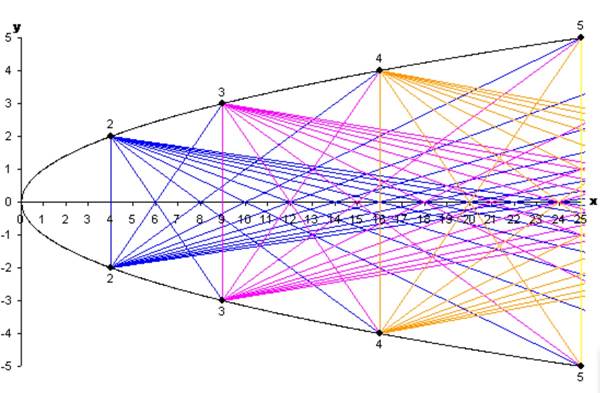
Aslında yukarıdaki adımları takip ederek kendi çiziminizi yaparsanız kolayca fark edeceğiniz gibi, x ekseninde üstünden çizgi ya da çizgiler geçen sayılar, referans aldığımız sayıların çarpımıdır. Bunun da nedenini yukarıda açıklamıştık. Bu durumda açıkta kalan sayılar da iki tamsayının çarpımından oluşmamaktadır. Bu da o sayıların asal olduğu anlamına gelecektir. Ayrıca göz atmak isterseniz: Arşimet’in Tüketme Yöntemi İle Bir Parabolün Alanını Hesaplaması
Kaynaklar ve İleri Okumalar İçin:
- Finding Primes using a Parabola; Yayınlanma tarihi: 17 Haziran 2021; Bağlantı: https://www.cantorsparadise.com
- Magic with a Parabola; https://people.math.harvard.edu
- Catching primes; Yayınlanma tarihi: 1 Ağustos 2008; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel