Hepimiz dönem dönem bir şeylerin en iyisini yapmak isteriz ancak çoğu zaman bunu nasıl yapacağımızı bilemeyiz. Bu gibi durumlarda bize gereken optimizasyon adı verilen bir matematik alanıdır. Bu alan genellikle bir şeyi maksimuma çıkarmayı (mesela bir tarladan yetiştirebileceğimiz mahsul miktarını) veya bir şeyi en aza indirmeyi (mesela bu mahsulleri yetiştirmek için ihtiyaç duyduğunuz su miktarını) hesaplamayı içerir.

Aslında gerçek hayatta karşılaşılan problemlerin çoğu optimizasyon ile ilgilidir. Çözülmesi gereken sorunu cebir kullanarak matematiksel olarak ifade edebiliyorsak o zaman bir çözüm bulma şansımız da yüksektir. Bunun nasıl çalışabileceğine dair bir fikir vermek için bir örnek üzerinden gidelim.
Bir Optimizasyon Problemi
Eski zamanlarda bir şövalye olsun ve bu şövalye oğullarına düğün hediyesi olarak 100 metrelik bir halatla kuşatabilecekleri en büyük toprak parçasını vermeyi vaat etsin. Ancak bir şartı var. Bu toprak parçasının bir kenarı, kendi arazisinin mevcut duvarlarından birisi olmalı. Aynı zamanda şekil dikdörtgen biçiminde olmalı. Oğullarından matematiği daha iyi olan en büyük parçayı alacak. Soruyu modellersek aşağıdaki gibi bir şekil elde ederiz.

Halatımız 100 metre. Genişlik için g, uzunluk içinde u harflerini kullanırsak elimizde 2g+u=100 biçiminde bir denklemimiz var. Buradan u=100-2g sonucunu elde edebiliriz. Amacımız alanı maksimum hale getirmek. Dikdörtgenin alan formülünü biliyoruz. Bu durumda uzunluk ile genişliği hemen çarpalım. Son durumda Alan=A= u.g= (100-2g).g=100g-2g2 biçiminde bir sonuca ulaşırız.
Gördüğünüz gibi yukarıda oluşturduğumuz alan formülümüz genişliğe bağlı. Bu noktada genişlik için değerler yazarak çeşitli alanlar hesaplayabilir, sonra da aralarından en büyük olanı seçemeye çalışılabiliriz. Ancak bu fazla pratik bir süreç sayılmaz. Bu noktada grafik çizmek daha iyi bir seçenek olacaktır. Aşağıdaki grafiğe baktığınızda görebileceğiniz gibi genişlik 25 olduğu zaman grafik maksimum noktasındadır. Grafiğe ya da bu değeri yerine koyarak 1250 metrekarelik maksimum alanı elde edebiliriz.
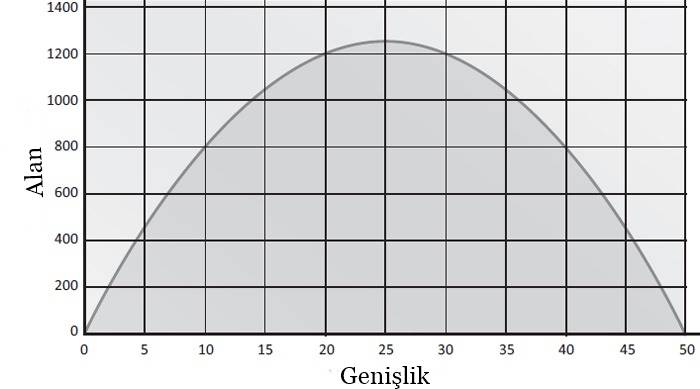
Sorunun Cebirsel Çözümü
Yukarıda aktardığımız süreç grafik çözümdü. Peki, maksimum ya da minimum değerler hesaplamalar yapmamız gerektiğinde başka yöntemler yok mu derseniz cevap evet olacaktır. Öncelikle A= 100g-2g2 denklemimizi A=-2( g2-50g) biçiminde düzenleyelim. İkinci dereceden bir denklemi tam kareye tamamladığınızda size maksimum ya da minimum noktasını söyleyebilir.
Lise yıllarından cebir bilginizi anımsarsanız ( g2-50g) tam kareye tamamlanınca (g-25)2 -625 biçiminde olur. Bunu yerine yazarsak A=-2[(g-25)2 -625] elde ederiz. Düzenlemeler sonucunda A=-2(g-25)2 +1250 buluruz. Elimizde bir alan formülü var ve içinde negatif bir bölüm barındırıyor. Alanı maksimum duruma getirmek için negatif kısmı mümkün oldukça küçük tutmak gerekiyor. Bu da g=25 olduğunda gerçekleşecektir.
Bu durumda alanımız ise yine 1250’dir. Yani şövalyenin oğlu genişliği 25 metre, uzunluğu ise 50 metre olan bir dikdörtgen yapabilir. Çözüm sizi mutlu ettiyse acele etmeyin. Bu yöntemler sadece ikinci derece denklemlerde işe yarar. Peki ya optimize etmek istediğimiz şekil daha farklı ve formül daha yüksek dereceden bir denklem ise ne yapacağız?
Optimizasyon ve Kalkülüs
Kalkülüs olmasaydı ne yörüngede dolaşan uydular olurdu, ne ekonomi kuramı, ne istatistik ne de optimizasyon hesabı. Değişimin olduğu her yerde karşımıza kalkülüs çıkar. Türev alma işlemi de bir değerin değişim oranını hesaplamamızı sağlayıp grafik çizmeden maksimum ve minimum noktalarını bulmamızda işimize yarar.
Türev almanın temel mantığı eğimi hesaplamaktır. Bir dağın zirvesinde ya da vadide de eğim yoktur. Düz bir şeyin eğimi sıfırdır. Eğimin sıfır olduğu noktalara bakarak da maksimum ya da minimum noktalarını bulmak mümkündür.
Türev almanın neden ve nasıl yapıldığının detayları bu yazının konusu değil. Merak edenler herhangi bir lise son sınıf ders kitabında ilgili kuralları bulabilirler. Türev alma en basit tanımı ile bir denklemi bir eğim denklemine dönüştürür. ( Kısa bir ön bilgi için bu yazımıza da göz atabilirsiniz: Türev Nedir? İntegral Nedir? Bu Kavramları Bilmek Neden Gereklidir?)
Bunu yapmak içinde en basit hali ile “xn” ifadesini “n.xn-1 ” haline getirir. Yukarıdaki örneğimizle hareket edersek A=100g-2g2 denkleminin türevi 100-4g biçiminde olacaktır. Bu bizim eğim denklemimizdir. Maksimum noktada eğim sıfır olacağı için de bu ifadeyi sıfıra eşitlersek g=25 sonucunu bir kere daha elde ederiz. Ayrıca bu konuya da göz atmanızı öneririz: Diferansiyel Denklemler Nedir? Bu Denklemler Ne İşimize Yarar?
Kaynaklar ve ileri okumalar:
- Optimization; https://tutorial.math.lamar.edu
- Chris Waring, Maths in Bite-Sized Chunk; ISBN: 978-1-78243-846-5; Michael O’Mara Books Limited 2018
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel