Geçtiğimiz yıllarda popüler bir Youtube kanalı olan Numberphile tarafından yayınlanan bir video interneti uzun süre meşgul etmişti. Videoya göre tüm doğal sayıları topladığınız zaman 1+2+3+4+… toplamının cevabı -1/12’ye eşit oluyordu. Peki tüm bunlar ne anlama geliyor? Bu yazıda Ramanujan toplamını anlamaya çalışalım.

Ramanujan Toplamı Nedir?
Hepsinden önce elbette tüm doğal sayıların sonsuz toplamı -1/12’ye eşit değildir. Bunu ispatlamamıza gerek yok. Elinize bir hesap makinesi alın ve arka arkaya sayıları toplamaya başlayın. Emin olun ki sonucunda -1/12 sayısını elde etmeyeceksiniz. İşte bu nedenle matematikçiler 1+2+3+4+… toplamının sonsuza ıraksadığını söyler daha basit bir biçiminde de sonucun sonsuz olduğu söylenir. Peki -1/12 sayısı nereden geliyor?

Bu yanlış sonuç aslında ünlü Hintli matematikçi Srinivasa Ramanujan‘ın 1913’teki çalışmasında ortaya çıktı Ama Ramanujan ne yaptığını biliyordu ve bunu yazmak için bir nedeni vardı. Yani aslında tam olarak yanlış bir hesaplama yapmamıştı.
Ramanujan Ne İle Uğraşıyordu?
Ramanujan çalışmalarını profesyonel matematik dünyasına duyurmak çok çabaladı, bunun için onlarca mektup yazdı. Hiç olumlu cevap alamasa da yazmaya devam etti. 1913’te Orders of Infinity kitabının büyüsüne kapılan Ramanujan, kitabın yazarı ünlü İngiliz matematikçi GH Hardy’ye (1877–1947) bir mektup yazdı.

Bir kez daha mektubunda, resmi eğitimden yoksun olduğunu belirtti, ancak bu sefer mektubuna çalışmalarından bazı örnekler ekledi. Hardy, hiçbir kanıtla desteklenmemiş güvenilmez iddialar ve tuhaf teoremlerle dolu bu mektuba başta önem vermedi. Ama mektubu üç saat boyunca inceleyen Hardy ve meslektaşı Littlewood sonunda karşılarında bir dahi olduğuna karar verdiler.
Ramanujan Tam Olarak Ne Yapmıştı?
Günümüzde bu mektupları inceleyerek matematikçinin aslında neyle uğraşmakta olduğu hakkında bir fikir sahibi olduk. Aslında kendisinin tam olarak ne yazdığını aşağıda görmeniz mümkündür.
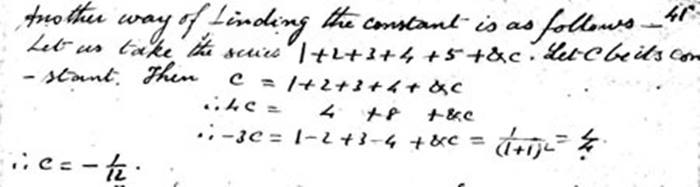
Gördüğünüz gibi mektupta c = 1 + 2 + 3 + 4 + 5 + 6 … yazıyor. Sonrasında da bazı işlemler yapıp Ramanujan toplamının sol tarafındaki sonucu elde ediyor. Bu işlemleri daha net biçimde aşağıda görmeniz mümkün.
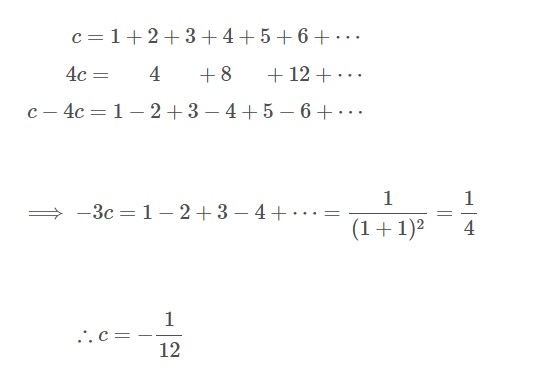
Gördüğünüz gibi Ramanujan seriyi bir ‘c’ sabiti olarak aldı ve c’den 4 çarpı c’yi çıkararak yeni bir seri elde etti. Ama nasıl oldu da : 1 – 2 + 3 – 4 + 5 – 6 + · · · = 1/4 sonucunu elde etti diyorsanız haklısınız. Bu sonucu aşağıdaki eşitlikten elde etmişti.
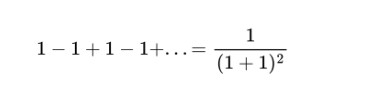
Şu anda kafanız karışmış olmalı. Bunun temel nedeni işin içine iki farklı serinin daha karışmış olmasıdır. Şimdi bu serileri teker teker ele alalım. Öncelikle 1 – 1 + 1 – 1 + · · · serisine bir göz atalım. Bu da sonsuz bir seridir ve yakınsak değildir. Aynı zamanda Grandi’nin serisi olarak da bilinir. Iraksak bir seri olduğundan kesin bir toplamı yoktur.
Ancak bu seriye parantezleri uygun şekilde yerleştirirsek sıfır sonucunu da elde edebiliriz. (1 – 1) + (1 – 1) + (1 – 1) + · · · = 0 + 0 + 0 + · · · = 0. Benzer biçimde birinci terimi bir kenara bırakarak parantezleri biraz farklı bir şekilde koyarsak “1” cevabını alırız. 1 + (1 – 1) + (1 – 1) + (1 – 1) + · · · = 1 + 0 + 0 + 0 + · · · = 1.
Gördüğünüz gibi oldukça kafa karıştırıcı bir seri. Zaten serinin ıraksak olması da bundan kaynaklanıyor. Ancak matematikçilerin bu seri için tuhaf bir cevabı daha var. Bu cevap da bize 1/2 sonucunu veriyor. Bu seriyi yakınsak bir seri olarak ele alırsak ve aşağıda da gördüğünüz cebirsel işlemleri uygularsak bu sonucu elde edebiliyoruz. Gördüğünüz gibi seriyi S olarak kabul edersek sonucumuz S=1/2 oluyor.
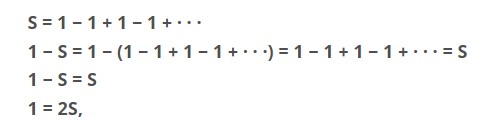
Ramanujan Toplamı Nasıl Sonuca Ulaşıyor?
Yukarıda Grandi serisi ile oynayarak bazı ilginç sonuçlar elde edebileceğimizi gördük. Aslına bakarsanız bunu çözmenin başka bir yolu daha var. Ancak bunun için sonsuz geometrik serileri anımsamalısınız. Anımsamıyorsanız aşağıda formülünü görüyorsunuz.
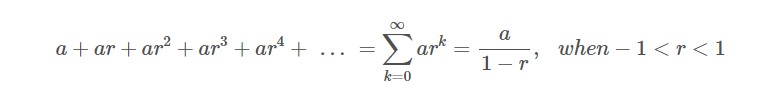
Yukarıdaki ifadeye a=1 ve r=-1 koyarsak ne olur? ( Tanım aralığından dolayı normal koşullarda r=-1 yazamayız. Ancak yazabildiğimizi düşünelim.). Bu durumda Ramanujan’ın oluştuğu sonuca kısmen ulaşmış oluruz.
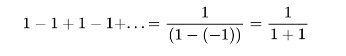
Eğer matematik ile aranız iyi ise, dizi yakınsamadığı için “toplamından” bahsetmenin yanıltıcı olduğunu düşünüyor olmanız olasıdır. Ancak sonucu kanıtlayacak daha resmi yöntemler de var. Grandi serisinin Cesáro toplamını yaparsak da yine 1/2 sonucunu elde ederiz. ( Bir serinin Cesáro toplamı, tüm kısmi toplamlarının ortalamasıdır.). Başka bir yöntem de Grandi serisinin grafiksel gösterimi olabilir. Ancak yazının daha karışık bir hal almaması için bu yöntemlere yazıda değinilmeyecektir.
O halde doğrudan bir sonraki seri olan 1 – 2 + 3 – 4 + · · ·’ e geçelim ve nasıl bir sonuç verdiğini görelim. Bu da ıraksak bir sonsuz seridir, gördüğünüz gibi kısmi toplamları herhangi bir sonlu limite doğru yönelmez. Bu seri öncekinden daha da karmaşıktır ve Cesáro toplamı yoluyla bile çözülemez. Daha da karmaşık matematiksel hesaplamalar gerektirir. Ancak çözümün basitleştirilmiş bir versiyonu aşağıdaki gibi olacaktır.
Ramanujan aşağıdaki ifadeyi yazmıştı. Biz de ikinci sıradaki sonuca ulaştık. Bu durumda ikisini birleştirerek ilginç bir sonuca ulaşmamız olası olacaktır. Bu durumda biz de çılgınca gibi gözükse de son denklemi yazabiliriz.
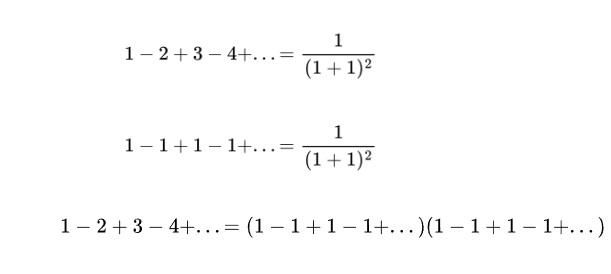
Sonsuz uzunlukta Grandi serisinin karesini nasıl alırız diye düşünebilirsiniz, karmaşık değil mi? Evet. Sonucu bulmak için sonsuz sayıda çarpma ve toplama yapılması gerekecektir. Ancak aşağıdaki biçimde düşünürsek bunu kolayca yapabiliriz. Çapraz gölgelemeyi takip ederek sayıları toplarsanız aşağıdaki seriyi elde edersiniz.
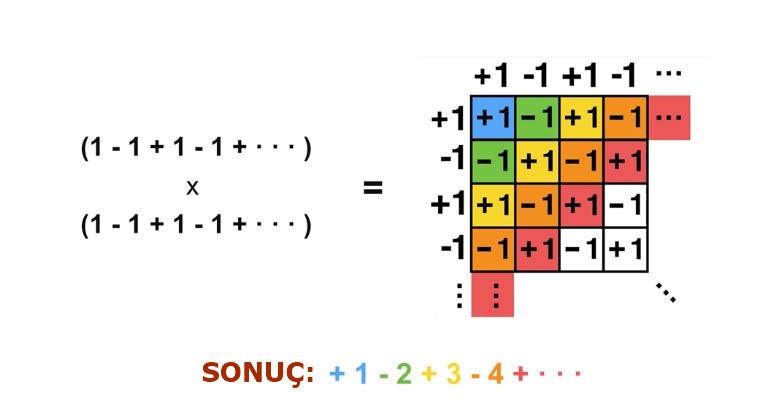
Tüm önemli sonuçları elde ettikten sonra Ramanujan’ın toplamına ve sonucuna geri dönelim. Artık bunu nasıl yazdığını kolayca anlayabilirsiniz.
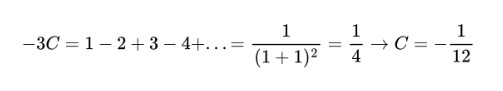
Ramanujan Toplamı Yanlış mı?
Bu sonuç büyüleyici görünebilir, ancak bu cevabı matematik ödevinize yazarsanız büyük ihtimal ile sıfır alırsınız. Sonsuz seriler ile sonlu toplamlarmış gibi işlem yapılmaz. Eğer yaparsanız sonuçta bu örnekte olduğu gibi tutarsız sonuçlara ulaşırsınız. Bunu elbette Ramanujan da biliyordu. Kendisi aslında Euler zeta fonksiyonu denen şeyin üzerinde çalışıyordu.
S(x)= 1 + 1/2x +1/3x + 1/4x … toplamının sonucu nedir? sorusunun cevabı bizi bu seriye götürecektir. Aslında her x > 1 için, S(x) ifadesinin iyi tanımlanmış, sonlu bir değeri vardır. Peki ama bu fonksiyona birden küçük bir değer yazarsanız ne olur? Mesela x=-1 için bir deneme yapalım. S(-1) = 1 + 1/2-1 +1/3-1 + 1/4-1 … yani S(-1) = 1 + 2 + 3 + 4 +… çıktı.
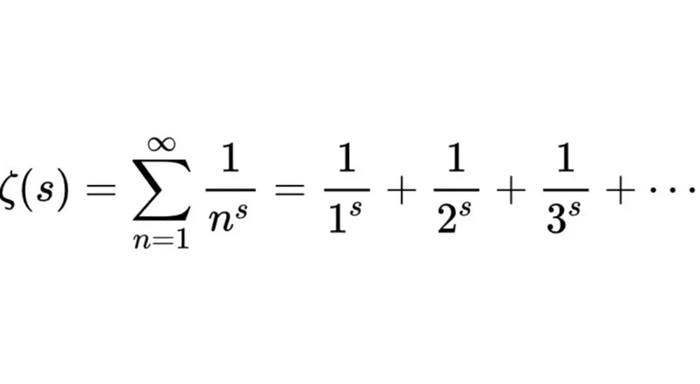
Karmaşık analiz kullanarak, Euler zeta fonksiyonunu 1’den küçük veya 1’e eşit olan sayılarda bir sonuç verecek şekilde genişletmenin bir yolu vardır. Bunu bize Bernhard Riemann göstermişti. Peki Zeta fonksiyonunda x=-1’i yerine yazdığınızda hangi değeri elde edersiniz? Tahmin etmiş olmalısınız. ζ(-1) =-1/12 kadardır.
Kaynaklar ve ileri okumalar için:
- When Infinity Is Actually a Small, Negative Fraction. Yayınlanma tarihi: 17 Ocak 2014. Kaynak site: Slate. Bağlantı: When Infinity Is Actually a Small, Negative Fraction
- Infinity or -1/12?; Yayınlanma tarihi: 18 Şubat 2014; Bağlantı: https://plus.maths.org
Matematiksel






Çalışmalarınız harika. Başarılarınız sürekli olsun, emeği geçenlere binlerce teşekkür. Eğer sizden öğrendiklerimi kullanırsa mutlaka sizi kaynak göstereceğim.
emeğinize sağlık çok açıklayıcı olmuş