Mantık Sorularını Çözerken Doğruluk Tablosu Yapmanın Kısa Yolu

Mantık soruları iki şekilde çözülebilir: Cebirsel yolla ve Doğruluk Tablosu yaparak. Tercih edilen yöntem cebirsel yoldur ama bu yolla her soruyu çözemeyebiliriz. Örneğin cebirsel yolla p ∧ ( p ∨ q) ifadesinin neye denk olduğunu bulmak pek de kolay olmayacaktır. Cebirsel yol çıkmaza girdiğinde imdadımıza doğruluk tablosu yetişir.

Doğruluk Tablosu Nedir?

Doğruluk tablosu, bir mantık ifadesinin tüm olası durumlarını sistematik bir şekilde değerlendirmek için kullanılan bir yöntemdir. Her doğruluk tablosunda yalnızca ifadede yer alan değişkenler (önermeler) için satırlar oluşturulur.

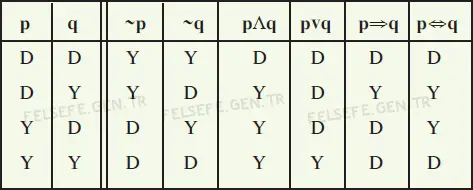
Örneğin, p∧(p∨q) ifadesi için yalnızca p ve q değişkenlerini değerlendirmek yeterlidir. Bu nedenle, n farklı değişken varsa, tablo 2ⁿ satır içerir. Bazı mantık bağlaçları için hızlı kararlar verebiliriz.

• p∨q→ En az biri doğru olduğunda sonuç doğrudur.
• p∧q → Her ikisi de doğruysa sonuç doğrudur.
• p⇒q→ Sadece “doğru → yanlış” olduğunda yanlış olur.
• p⇔q → Her iki önerme aynı olduğunda doğrudur.

Bu temel kuralları bilmek, tablonun satırlarını tek tek yazmak yerine sonuçları zihinsel olarak doldurmamıza yardımcı olur.

Soru:  p ∧ ( p ∨ q) ifadesinin en sade şeklini bulunuz.

Çözüm: İç parantezdeki p ve q’nun altına doğruluk değerlerini yazarak başlıyoruz. Şekli inceleyiniz:

Sonra parantez içindeki ∨ bağlacını işliyor ve bulduğumuz sonucu sembolün hemen altına yazıyoruz.

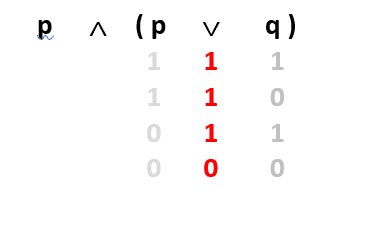
Şimdi en baştaki p’nin altını dolduruyoruz.

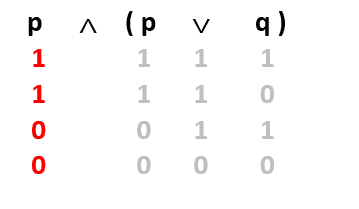
Ve son olarak en soldaki ∧ bağlacının işlemini yaparak sonucunu sembolün altına yazıyoruz.

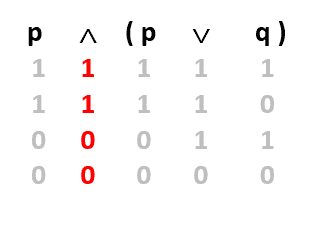
Bulduğumuz sonucun p önermesine denk olduğunu görünüz. O halde sorumuzun cevabı p’dir. Yani p ∧ ( p ∨ q)=p biçimindedir. Aynı şeyleri üç önerme için de yapabiliriz. Bu kez: p=11110000, q=11001100 ve r=10101010 almalıyız. (Önerme sayısı 3 olduğunda satır sayısı 2³=8 olur.)

Soru: p ⇒ [ p ∨ ( p‘ ∧ r)] ∧ q ifadesinin en sade halini bulunuz.

Çözüm: Sütunları doldurmaya en içteki parantezden başlıyoruz. Şekli inceleyiniz:

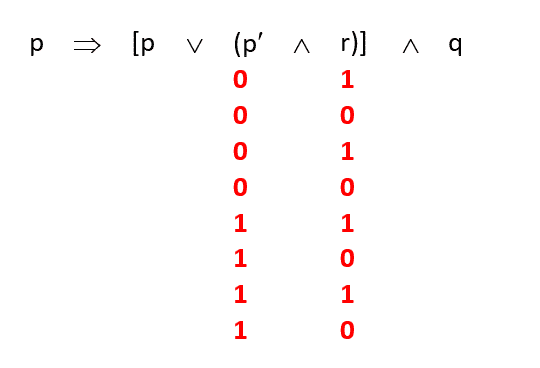
Sonraki adım ∧ bağlacının altına işlem sonucunu yazmak:

Şimdi ∨ bağlacının altını doldurabiliriz. Ama önce p’nin altını dolduruyoruz.

Şimdi de veya bağlacı dolduruluyor:

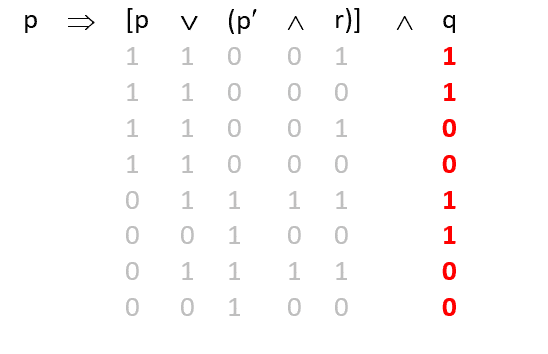
 Sıra q’da:

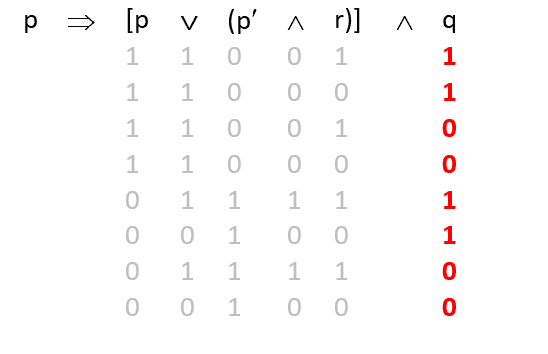
Sıra geldi en sağdaki ve bağlacına.

Şimdi en soldaki p’yi dolduruyoruz:

Ve son olarak ise bağlacını işliyoruz:

Kırmızı sütun işlemin sonucudur. Peki, ama bu sütun hangi önermeye denktir? Biraz dikkatli bakarsak, bunun p ⇒q olduğunu anlarız. (Neden?) O halde sorumuzun cevabı: p ⇒ [ p ∨ ( p‘ ∧ r)] ∧ q = p ⇒ q olur.

Bağlaçları Hatırlamak İçin Kolay Bir Yöntem

Yazımızın bu bölümünde de kısa bir şekilde mantık dersinde kullanılan temel bağlaçları ele alacak ve onlarla yapılan mantıksal işlem sonuçlarını hatırlamanın kolay yollarını göstereceğiz.

Veya: Veya bağlacını toplama işlemi olarak düşünebilirsiniz. (Tabi 1 + 1 = 1 olduğunu kabul etmek şartıyla.)

• 1 ∨ 1 = 1 yani 1 + 1 = 1
• 1 ∨ 0 = 1 yani 1 + 0 = 1
• 0 ∨ 1 = 1 yani 0 + 1 = 1
• 0 ∨ 0 = 0 yani 0 + 0 = 0

Ve: Ve bağlacını çarpma işlemi olarak düşüneceğiz.

• 1 ∧ 1 = 1 yani 1 × 1 = 1
• 1 ∧ 0 = 0 yani 1 × 0 = 0
• 0 ∧ 1 = 0 yani 0 × 1 = 0
• 0 ∧ 0 = 0 yani 0 × 0 = 0

İse: ⇒ bağlacını ≤ olarak düşüneceğiz.

• 1 ⇒ 1 = 1 yani 1 ≤ 1 → 1 (Doğru)
• 1 ⇒ 0 = 0 yani 1 ≤ 0 → 0 (Yanlış)
• 0 ⇒ 1 = 1 yani 0 ≤ 1 → 1 (Doğru)
• 0 ⇒ 0 = 1 yani 0 ≤ 0 → 1 (Doğru)

Ancak ve Ancak: ⇔ bağlacını = olarak düşüneceğiz.

• 1 ⇔1 = 1 yani 1 = 1 → 1 (Doğru)
• 1 ⇔ 0 = 0 yani 1 = 0 → 0 (Yanlış)
• 0 ⇔ 1 = 0 yani 0 = 1 → 0 (Yanlış)
• 0 ⇔ 0 = 1 yani 0 = 0 → 1 (Doğru)

Ya da: Ya da bağlacını ≠ olarak düşüneceğiz.

• 1 ⊻ 1 = 0 yani 1 ≠ 1 → 0 (Yanlış)
• 1 ⊻ 0 = 1 yani 1 ≠ 0 → 1 (Doğru)
• 0 ⊻ 1 = 1 yani 0 ≠ 1 → 1 (Doğru)
• 0 ⊻ 0 = 0 yani 0 ≠ 0 → 0 (Yanlış)

Bağlaçların Pratik Uygulamaları İle İlgili İki Örnek

• Örnek1: 1 ⇒ [ 1∨ (0 ∧ 1)] ∧ 0 işleminin sonucu nedir?
• Çözüm: 1 ≤ [ 1 + (0 × 1)] × 0 = 1 ≤ [ 1 + 0] × 0 = 1 ≤ [ 1 ] × 0 = 1 ≤ 0 = 0 (yanlış)

• Örnek 2: [ 1 ⇒ (1 ⇒ 0) ] ⇒ [ ( 0⇒ 1 ) ⇒ ( 1 ⇒ 1) ] işleminin sonucu nedir?
• Çözüm: [1 ≤ (1 ≤ 0)] ≤ [( 0 ≤ 1 ) ≤ (1 ≤ 1)] = [ 1 ≤ 0 ] ≤ [ 1 ≤ 1 ] = 0 ≤ 1 = 1 (Doğru)

Bu iki yöntem yardımı ile mantık dersindeki sorunlarınızın bir kısmının çözüleceğini düşünüyoruz. Şimdiden kolay gelsin. Ayrıca yazının devamında göz atmanızı öneririz. Önermeler Mantığında İse Bağlacını Anlamanın Kolay Yolu

Size Bir Mesajımız Var!

Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel