Ramanujan ölmeden önce, ilginç sonuçlar doğuran bir teori geliştirmekle meşguldü. Sadece yayınlayacak kadar uzun yaşamamıştı. Keşfin bir ucunda bir çoğumuzun adını duyduğu 1729 sayısı diğer adıyla Taksi sayılar bulunmaktaydı.

Matematik tarihi boyunca Srinivasa Ramanujan’a uzaktan yakından benzeyen hiç kimse olmadı. Belki de bu nedenle hakkında uzun metrajlı bir film çekilen ender matematikçilerden biri oldu. Ramanujan’ın kalıpları görme konusunda olağanüstü bir yeteneği vardı. Özellikle sayılar teorisinin modüler formlar adı verilen bir bölümünde uzmandı.
Ancak onun zamansız ölümü matematik tarihine büyük bir darbeydi. Bir kutu el yazması ve üç defter. Efsanevi Hintli matematikçi Srinivasa Ramanujan’ın çalışmalarından bize geriye kalanlar bunlardan ibaret. Ancak bu kadarı ile bile bizleri şaşırtmaya devam ediyor.

Emory Üniversitesi’nden iki matematikçi, onun sararmış sayfaları içerisinde geçtiğimiz yıllarda büyüleyici bir keşif yaptı. Bu keşif Ramanujan’ın zamanının çok daha ilerisinde olduğunu bir kere daha gösterdi. Ayrıca matematik tarihindeki önemli noktalar arasında güzel bir bağlantı sağladı.
Ramanujan İle 1729 Sayısı Arasındaki İlişki Nedir?
Taksi sayılar ile matematik dünyası G.H. Hardy tarafından anlatılan anekdot ile tanıştı. Anekdot şu şekildeydi: “Bir keresinde Putney’de hasta olduğu zaman (Ramanujan’ı) görmeye gittiğimi anımsıyorum. 1729 numaralı bir taksi ile yolculuk yaptım ve bu sayının bana oldukça sıkıcı geldiğini söyledim. ‘Hayır’ diye yanıtladı, ‘Çok ilginç bir sayı. İki küpün toplamı olarak iki farklı şekilde ifade edilebilen en küçük sayıdır.’ “
Ramanujan’ın sayılar hakkında harika bir hafızası ve sezgisi vardı. Ramanujan’ın söylemeye çalıştığı da aslında şuydu. 1729=13+123=93+103. İki küpün toplamı olarak yazılacak daha küçük bir tamsayı yoktur. Bu sonuç size anlamsız geldiyse, yanılıyorsunuz. Ramanujan aslında 1993’te Andrew Wiles tarafından kanıtlanmış olan Fermat’ın Son Teoremi nedeniyle iki küpün toplamıyla ilgilenmekteydi. Sonucunda notları arasından bulunan aşağıdaki sararmış sayfa da bunun bir kanıtıydı.
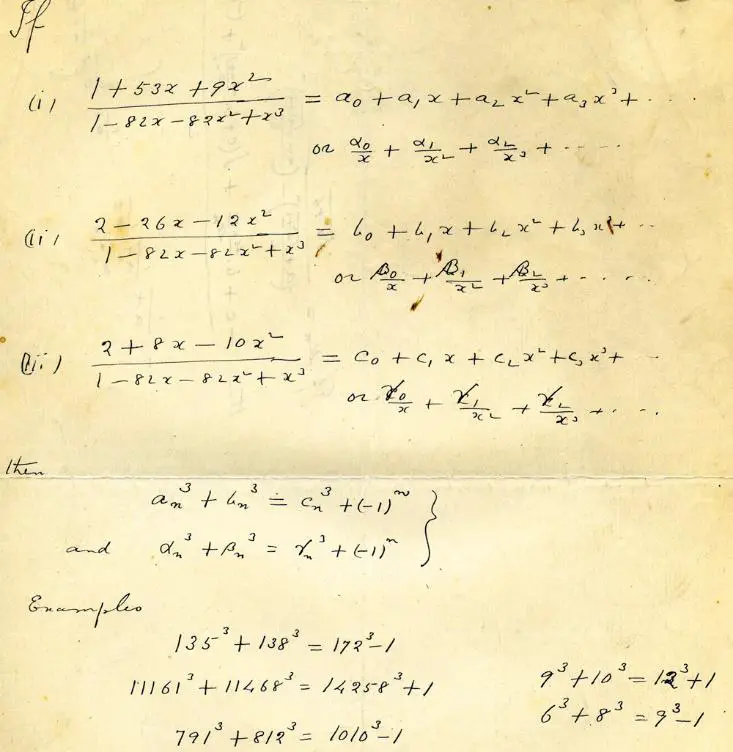
1637’de Pierre de Fermat’ın şaşırtıcı derecede basit bir varsayımda bulunmuştu. Fermat, n 2’den büyük herhangi bir tam sayı ise, an + bn = cn denklemini sağlayan sıfırdan başka a, b, c tam sayısı olmadığını not etmişti. Fermat ayrıca bu ifadeyi kanıtladığını da iddia ediyordu. Ancak ifadesine göre bu kanıtı yazacak kadar yeri yoktu.
Ramanujan’ın Notlarında Fermat’ın Son Teoremi
Matematikçilerin kalbini çalan şey bu iddia ve söz konusu problemin basitliği oldu. Fermat’ın ispatını tekrar keşfetmek zamanla matematikçiler için bir meydan okumaya dönüştü. Ancak yüzyıllar süren bir ispat bulma çabası sonuçsuz kalacaktı. Bu sorun nihayetinde Andrew Wiles tarafından kanıtlandı. Ancak Ramanujan bunu görecek kadar uzun yaşamamıştı.
Ramanujan x, y ve z’nin tam sayı değerleri için x3 + y3 = z3 ± 1 biçimindeki denklemleri araştırıyordu. Sonsuz sayıda çözüm olduğunu göstermişti. Ayrıca çözümleri elde etme prosedürünün ana hatlarını da çizmişti. Yukarıda gördüğünüz defterindeki 93 + 103 = 123 + 1, 63 + 83 = 93 – 1 işlemleri özel çözümleri içeriyordu. Sondaki 1 sayısını da 13 olarak düşündüğünüzde bu eşitlikler Taksi Sayılarını veriyordu. Ama bu kadarla da kalmadı.
Emory Üniversitesi’nde sayı teorisyeni Ken Ono ve lisansüstü öğrencisi Sarah Trebat-Leder Ramanujan’ın çalışmalarındaki diğer sayfalara göz gezdirirken, ilginç bir şeye daha rastladılar. Onun eliptik eğriler teorisini incelediğini fark ettiler. Eliptik eğriler, belirli bir biçimdeki denklemlerin çözümlerinin incelenmesini ifade eder. Özellikle sayı teorisinde önemlidir ve güncel araştırmaların önemli bir alanını oluşturur. Eliptik bir eğrinin denklemi y2 = x3 + ax + b biçiminde olur. Grafiği de genellikle aşağıdaki gibidir.
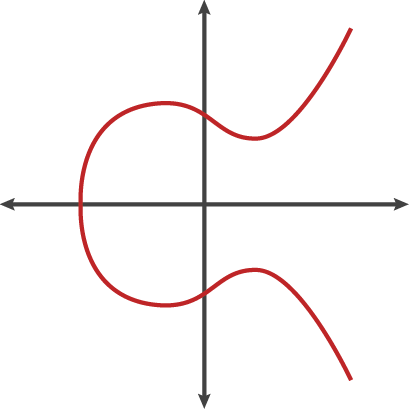
Eliptik eğriler, 1990’larda Andrew Wiles’ı nihayete erdiren kanıtında önemli bir role sahip olmuştu. Ancak Ramanujan, Wiles’ın izlediği yoldan gitmemişti. Bunun yerine eliptik eğrilerden daha karmaşık bir nesne keşfetmişti.
Bu tür nesneler Ernst Kummer, Erich Kähler ve Kunihiko Kodaira’nın katkılarıyla kırk yıl sonra yeniden keşfedilecekti. Devamında da K2 dağı kadar tırmanması zor olduğu için K3 yüzeyleri adı ile anılmaya başlanacaktı.
Taksi Sayılar Nedir?
Ramanujan, K3 yüzeyi için formüller geliştirmek için 1729 sayısı ve eliptik eğrileri kullanıyordu. Matematikçiler bugün hala K3 yüzeylerini manipüle etmek ve hesaplamak için mücadele ediyor. Bu yüzden Ramanujan’ın başından beri bu sezgiye sahip olması büyük bir sürprizdi. Bunun sonucunda da 1729 gibi başka sayıların olup olmadığı da araştırılmaya başlandı. Sonrasında da daha fazlası bulundu.
Genel hali ile Taksi sayılarını Tα (n), iki pozitif küpün n farklı şekilde toplamı olarak ifade edilebilen en küçük sayı olarak tanımlanır. Taksi sayılar denmesinin nedeni de yukarıda aktardığımız anekdottur. Hardy’nin bu hikayeyi sık sık tekrarlaması, 1729’un matematikte en iyi bilinen sayılardan biri olmasını sağladı.
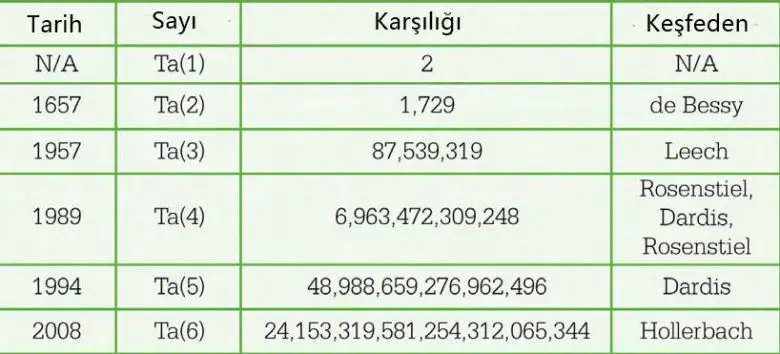
Aslında bu sayının benzersiz özelliklerini ilk not eden Ramanujan değildi. Fransız matematikçi Bernard Frénicle de Bessy de 1600’lerde aynı konuda çalışmalar yapmıştı. Ancak Taksi hikayesi sonraki matematikçilerin konuyu incelemesine ve uygulama alanını genişletmesine sebep oldu.
Tα (n) ‘nin tüm n değerleri için var olduğunu aslında biliyoruz. Hatta 2014 yılına kadar ilk altı taksi sayı yani Tα (1), Tα (2), …, Tα (6) bulundu. Özellikle son üç sayının hesaplanabilmesi için süper bilgisayarların kullanılması gerekiyordu.
Sonuç olarak
Günümüzde daha büyük Taksi sayıları içinde aramalar devam etmektedir. Bu sayıları gördükten sonra bir işe yarayıp yaramadıkları sorusu muhtemel aklınıza gelecektir. Bu sayılar matematikte pratik anlamda fazla bir işe yaramaz. Ancak matematikçiler bu tür arayışlarını sürdürürken de bununla fazla ilgilenmez.
Kaynaklar ve ileri okumalar:
- Plus Magazine, Marianne Freiberger, Ramanujan Suprises Again, Yayınlanma tarihi: 3 kasım 2015. Bağlantı: Ramanujan Suprises Again
- How a ‘rather dull’ taxi number inspired. Ramanujan to make a math discovery decades ahead of his time. Yayınlanma tarihi: 15 Ekim 2015. Kaynak site: ZME Science. Bağlantı: How a ‘rather dull’ taxi number inspired. Ramanujan to make a math discovery decades ahead of his time
- Abramovich, Sergei & Sugden, Stephen. (2005). Spreadsheet Conditional Formatting: An Untapped Resource for Mathematics Education. Spreadsheets in Education (eJSiE). 1.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










