“Bu kapılardan birinin arkasında hayallerinizin ödülü var! Ama iyi düşünün. Diğer iki kapıyı seçerseniz hiçbir şey kazanamayacaksınız. ” cümlesi ile başlayan Monty Hall problemi, matematikteki en ünlü problemlerden biridir.

Problemin kaynağı ABD televizyonlarında 1963’den 1977’ye kadar yayında kalan Let’s Make A Deal (Bizde ki Var mısın, Yok musun yarışmasının atası denilebilir) isimli bir yarışma programıdır. Monty Hall ise bu yarışmaya sunan kişinin adıdır.
Bu problem aslında matematiğin sezgilere aykırı halinin iyi bir örneğidir. Bu nedenle uzun zamandır gündemde varlığını sürdürmektedir. Bu problemin cevabı “21 Filminde” de kullanılmış sonrasında da sevgili seçiminizde neden değişiklik yapmanız gerektiğinin bir nedeni olarak bile savunulmaya başlanmıştır.

Yarışma programında yarışmacılara üç kapalı kapı gösterilmektedir. Bunlardan birinin arkasında araba gibi değeri yüksek bir ödül yer alır. Yarışmacılar doğru kapıyı açar ise ödülü kazanır. Aksi takdirde ise hiçbir şey kazanamazlar. Daha sonra yarışmacılardan bir kapı seçmeleri istenir ve seçimin ardından geriye kalan iki kapıdan biri açılır. Şimdi seçtiğiniz kapı ve seçilmemiş diğer kapılar var. Bunlardan birinde büyük ödül olduğu kesin. Kararınızı değiştirmek ister misiniz?
Monty Hall Problemi Nedir?
Yukarıdaki senaryo şu soruyu gündeme getiriyor: Başlangıçta seçtiğiniz kapıdan geçiş yaparsanız kazanma olasılığınız daha mı yüksek? Bu soru, Amerikalı istatistikçi Steve Selvin tarafından 1975 yılında The American Statistician dergisine yazdığı bir mektupta ortaya atıldı. Daha sonrasında da Monty Hall problemi olarak bilinmeye başlandı.

Bu soru Parade dergisinin 1990 sayısındaki Marilyn vos Savant’ın Ask Marilyn sütununda sunulduğunda popüler hale geldi. “En yüksek IQ’ya sahip kadın” kategorisinde Guinness dünya rekorunu kırarak üne kavuşan Marilyn vos Savant, verdiği cevapta, yarışmacının her zaman değişiklik yapması gerektiğini savunacaktı. Ona göre bu durumda, yani orijinal seçimlerine sadık kalmalarına kıyasla, kazanma olasılıkları iki kat daha fazla oluyordu. Verdiği cevap aşağıdaki gibiydi.
“Seçtiğimiz kapıyı değiştirmek uygun olacaktır. Çünkü soruda da anlatıldığı gibi fikir değiştirip 2 numaralı kapıyı seçmek bize arabayı almak için 2/3 oranında bir şans sağlar. Eğer ilk seçimimiz olan 1 numaralı kapıda kalsaydık bu oran 1/3 olacaktı.”
Bu basit cevap beklenmedik bir kargaşaya neden oldu. Tartışma sadece derginin sadık takipçileri arasında patlak vermedi. Kısa sürede akademik ve bilimsel çevrelere de sıçradı. Dergiye en az 10.000 mektup geldi. Bunların çoğu vos Savant’ın cevabına şiddetle karşı çıkıyordu. Bu kişilerin çoğu da matematikçilerdi.
Kendisine yapılan tüm baskılara rağmen Savant düzeltme yapmayı ret edecekti. Sonrasında da problemin çözümü hakkında dört köşe yazısı daha yazdı. Aslında soruyu analiz eden pek çok uzman o zamandan beri vos Savant’ın cevabının doğru olduğunu kabul ediyor. Yani mantığa aykırı gibi gözükse de seçtiğiniz kapıyı değiştirirseniz kazanma olasılığınız iki kat daha fazla olacaktır.
Monty Hall Probleminin Çözümü Nedir?
Bu sorunun cevabını ve değiştirmenin neden kazanma olasılığınızı iki katına çıkardığını anlamak için kapıların arkasını görebildiğimizi kabul edelim. Ve ayrıca keçi yerine araba kazanmak istediğinizi kabul edelim. Ayrıca yarışma sunucusunun ödülün hangi kapının ardında olduğunu bildiğini unutmayın. Bu durumda aşağıdaki senaryolar karşımıza çıkacaktır.
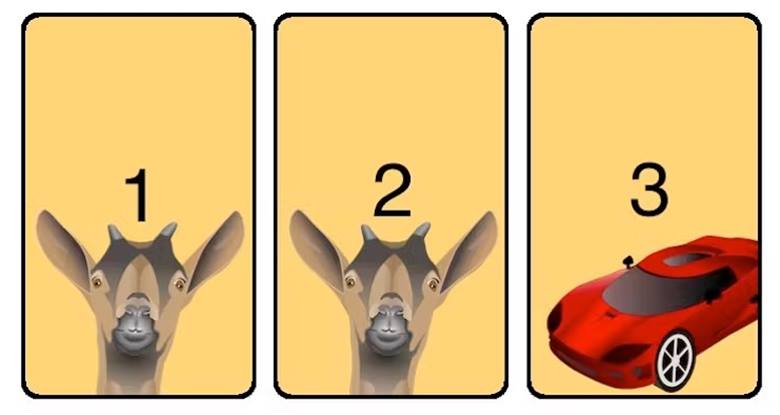
- 1. Durum: Yarışmacı 1. kapıyı seçerse, yarışma sunucusu 2. kapıyı açar. Bu durumda eğer seçtiğiniz kutuyu değiştirseydiniz arabayı kazanacaktınız.
- 2. Durum: Yarışmacı 2. kapıyı seçerse, yarışma sunucusu 1. kapıyı açar. Bu durumda eğer seçtiğiniz kutuyu değiştirseydiniz arabayı kazanacaktınız.
- 3. Durum: Yarışmacı 3. kapıyı seçerse yarışma sunucusu diğer kapılardan birinin arkasında ne olduğunu gösterecektir. Bu durumda geçiş yapmak araba ödülü kaybetmenize neden olacaktır.
Bu durumda, başlangıçta seçtiğimiz kapının arkasında bir keçi olduğu sürece, seçtiğimiz kapıyı değiştirmenin her zaman kazançla sonuçlanacağını görebiliriz. Bu durum üçte iki oranında gerçekleştiği için ve başlangıçta da herhangi bir seçim şansınız üçte bir olduğu için, seçtiğiniz kapıyı değiştirmek kazanma şansınızı iki katına çıkaracaktır.
Hala ikna olmadıysanız bunu üç tane kahve fincanını kapı gibi düşünerek, bir arkadaşı yardımı ile kendiniz de deneyebilirsiniz. Yeterince uzun oynadığınız zaman seçtiğiniz fincanı değiştirmenin sizin için daha avantajlı olduğunu fark edeceksiniz. Aslına bakarsanız, matematikçi Paul Erdős da başta ikna olmamıştı. Ancak konu ile ilgili bir bilgisayar simülasyonunu inceledikten sonra ikna olacaktı.
Monty Hall Problemini Daha iyi Anlamak İçin
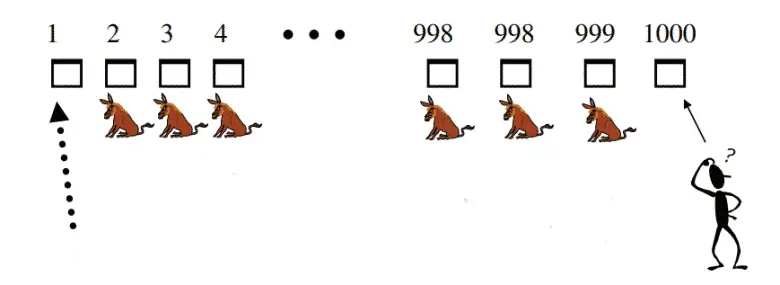
Monty Hall probleminde üç kapı yerine bir milyon kapı olursa çözüm daha iyi anlaşılır hale gelecektir. Sadece bir kapıda büyük ödül, diğer 999.999 kapıda keçi olsun. Yarışmacı bir kapı seçsin. Sunucu, arabanın olduğu kapının dışında kalan diğer 999.998 kapıyı açsın ve yarışmacıya seçimini değiştirip değiştirmek istemediğini sorsun.
En başta, yarışmacının büyük ödülü kazanma olasılığı milyonda bir idi. Yani yarışmasının başlangıçtaki tahmini 999.999/1.000.000 olasılıkla yanlıştı. Bu olasılık her zaman korunacaktır. Son durumda 999.999/1.000.000 olasılıkla büyük ödül açılmayan kapıda olacaktır. Yani seçtiğiniz kapıyı değiştirmek kesinlikle çok daha avantajlıdır.
Sonuç olarak
Monty Hall probleminin tarihçesi aslında 1960’lardan çok daha öncesine dayanmaktadır. Bertrand’ın kutu paradoksu ya da Üç Kutu Paradoksu olarak bilinen soru, Monthy Hall probleminin temelini oluşturur. Bu paradoks Fransız matematikçi Joseph Louis François Bertrand (1822–1900) tarafından, 1889 yılında yayınlanan “Calcul des probabilités” adlı kitabında ortaya atılmıştır.

Paradoks Monty Hall problemine benzer bir biçimde, içerikleri başlangıçta bilinmeyen üç kutuyla başlar. Kutuların her birinde iki çekmece vardır. Bir kutunun iki çekmecesinin her birinde birer altın bulunur. İkinci kutunun iki çekmecesinde de birer gümüş para bulunur. Üçüncü kutuda ise bir çekmecede gümüş para, diğer çekmecede de altın var.
Rasgele bir kutu seçtikten sonra eğer kutudan rasgele bir çekmece çektiğimizde altın bulursak, diğer çekmecedeki paranın da altın olmasının olasılığı nedir? Gördüğünüz gibi bu soru Monthy Hall problemine oldukça benzerdir. Problemin çözümü için de bu yazımıza göz atmanız gerekmektedir.
Kaynaklar ve ileri okumalar:
- The Monty Hall problem: going with your gut will get your goat. Yayınlanma tarihi: 12 Haziran 2013. Kaynak site: Conversation. Bağlantı: The Monty Hall problem: going with your gut will get your goat
- A Point of View: Why embracing change is the key to happiness. Yayınlanma tarihi: 8 Ekim 2013. Bağlantı: A Point of View: Why embracing change is the key to happiness2
- Myths of maths: The Monty Hall problem; yayınlanma tarihi: 23 mart 2020. Bağlantı: Myths of maths: The Monty Hall problem/
- Here’s the easiest way to understand the Monty Hall problem. The mathematics puzzle about goats that even PhD-holders get wrong; Yayınlanma tarihi: 3 Aralık 2016. Bağlantı: Here’s the easiest way to understand the Monty Hall problem. The mathematics puzzle about goat/
Matematiksel