Bir pipette kaç delik vardır? Bir mi, yoksa iki mi? Bu sorunun cevabı ilk bakışta son derece basit gibi görünüyor, değil mi? Ancak, konu üzerine düşünenler arasında farklı ve hatta çelişkili görüşler bulunuyor. Bazı kişiler pipetin sadece bir deliği olduğunu savunurken, diğerleri iki deliği olduğunu öne sürüyor. Hatta, pipetin sonsuz deliğe ya da hiçbir deliğe sahip olduğunu iddia edenler bile var!

Konuya ilgisi olmayan bir kişi için “delik” denildiğinde, aklına gündelik hayatta görmeye alışık olduğu şeyler gelir. Ancak, matematikçiler için delik, tamamen farklı bir anlam taşır ve topoloji adı verilen bir matematik dalıyla ilgilidir.
Fakat burada bir sorun vardır: Topolojide bile “delik” kavramının birbirinden farklı tanımları bulunur. Bu durum, bazı nesnelerin kaç delik barındırdığı sorusunun, sorduğunuz kişinin benimsediği tanıma bağlı olarak değişmesine yol açar. Bu nedenle, bir pipetin kaç deliği olduğu sorusu göründüğünden çok daha karmaşık hale gelir.

Matematiksel Anlamda Delik Nedir?
Geometride, daireler ve çokyüzlüler gibi şekiller katı ve sabit nesnelerdir. Uzunlukları, açıları ve alanları gibi belirli ölçümleri vardır. Ancak topolojide şekiller esnek yapıdadır. Örneğin, küre ve küp geometrik olarak farklı nesneler olsa da, topolojik açıdan bir farkları yoktur.
Bu konuya ilişkin ünlü bir örnek, bir simidin topolojik olarak bir kahve fincanıyla aynı şey olmasıdır. Bu dönüşümde değişmeyen şey, deliktir. Simidin ortasındaki delik, kahve fincanının sapındaki delik haline gelir. Başka bir deyişle, delik yok olmaz; sadece şekil değiştirir. Topolojik olarak iki nesnenin aynı kabul edilmesi için bu nesnelerdeki delik sayısının eşit olması gerekir.

Bir tişört ile bir pantolonun farklı olduğuna dair matematiksel bir kanıta bir gün ihtiyaç duyarsanız, bu kanıtı topoloji sağlayabilir. Çünkü bu iki nesne, farklı sayıda deliğe sahiptir.
Topolojide Delik Sayısı İle İlgili Sorun Nedir?
18. yüzyılda, matematikçi Leonhard Euler, topoloji alanında önemli araştırmalara başladı. 1750 yılında, tüm zamanların en büyük teoremlerinden biri olarak kabul edilen bir ilişkiyi ortaya koydu. Euler, katı bir cismin F yüzü, E kenarı ve V köşesi varsa, F + V = E + 2 eşitliğini sağlandığını keşfetti.
Bu formülü bir küp üzerinde test edelim. Küpün 6 yüzü, 12 kenarı ve 8 köşesi vardır. Yüzlerin ve köşelerin toplamı 6 + 8 = 14 eder. Bu, 12’den tam olarak 2 fazladır ve Euler’in formülünü doğrular. Ancak bu formül her çokyüzlü için geçerli midir? Görünen o ki, hayır.
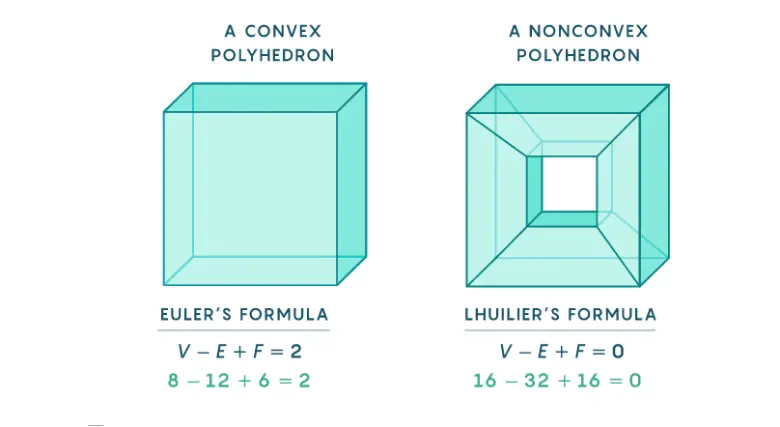
Örneğin, bir resim çerçevesini ele alalım. Çerçevenin 6 yüzü, 32 kenarı ve 16 köşesi vardır. Ancak bu durumda, yüzler ve köşelerin toplamı ile kenarlar arasındaki ilişki değişir. F + V – E = 0 olur. Peki, bu çelişkinin sebebi nedir?
Bunun nedeni, çerçevenin içinde bir delik barındırmasıdır. Euler’in formülü, deliklerin varlığına göre düzenlenmiştir. Eğer bir çokyüzlüde g adet delik varsa, eşitlik şu şekle dönüşür: F+V-E=2-2g
Bu, topolojinin temel ilkelerinden birini ortaya koyar: Deliklerin varlığı, nesnenin geometrik ilişkilerini değiştirir. Bu şekilde, Euler’in teoremi, sadece çokyüzlüler değil, aynı zamanda topolojik nesneler için de bir temel oluşturur.
Bir Pipetin Kaç Tane Deliği Vardır?
Bu noktaya kadar konuya aşina olmayan okuyucuların, matematikçilerin “delik” dediğinde ne anladığını kavraması önemlidir. Yazının devamında mümkün olduğunca teknik olmayan bir dil kullanacağımız için daha fazla bilgi edinmek isteyenlerin bir topoloji ders kitabını incelemesi önerilir. Şimdi, konumuza geri dönelim.
İçinde delik bulunmayan bir şekli tanımlamak oldukça kolaydır. Bu tür yüzeylerde, F + V – E her zaman 2 eşit olur. Aynı zamanda, bu durumun tersi de doğrudur: Eğer F + V – E = 2 ise, bu çokyüzlü bir küre olacak şekilde deforme edilebilir. Ancak, F + V – E = 0 olduğu durumlarda, örneğin resim çerçevesi örneğimizde, şekli bir küreye dönüştürmek mümkün değildir.
Delik kavramının tam bir matematiksel tanımını yapmak zor olsa da yukarıda verdiğimiz formül yeniden düzenlenerek delik sayısı şu şekilde hesaplanabilir: g = -(F + V – E – 2) / 2
Peki, az önceki formülü pipetimize nasıl uygularız? Sonuçta bir pipet, aslında bir silindirin yuvarlanmış halidir. İlk bakışta, pipetin iki deliği varmış gibi görünebilir. Ancak, pipeti diklemesine kesip açtığınızda bu iki delik tamamen yok olur ve elinizde yalnızca bir dikdörtgen yüzey kalır.
Örneğin, bir bardağı ele alalım. Bardağın ağzı açıktır, içine bir şey koyabilirsiniz; ancak topolojik açıdan kulpsuz bir bardakta delik yoktur. Bu nedenle, pipetin iki deliği olduğunu söyleyemeyiz. Peki, o zaman pipette kaç delik var?
Şimdi pipetimizin esnek olduğunu hayal edelim ve şeklini deforme edelim. Üstten bastırarak, pipetin üst açıklığı ile alt açıklığını birleştirelim. Bu durumda, pipet bir simide benzeyecektir. Bu bakış açısına göre, pipetimizin bir deliği olduğunu söyleyebiliriz.
Ancak, bu açıklama size yeterli gelmediyse, başka bir matematikçinin delik kavramını nasıl tanımladığına bakalım.
Deliğin Alternatif Bir Tanımı Nedir?
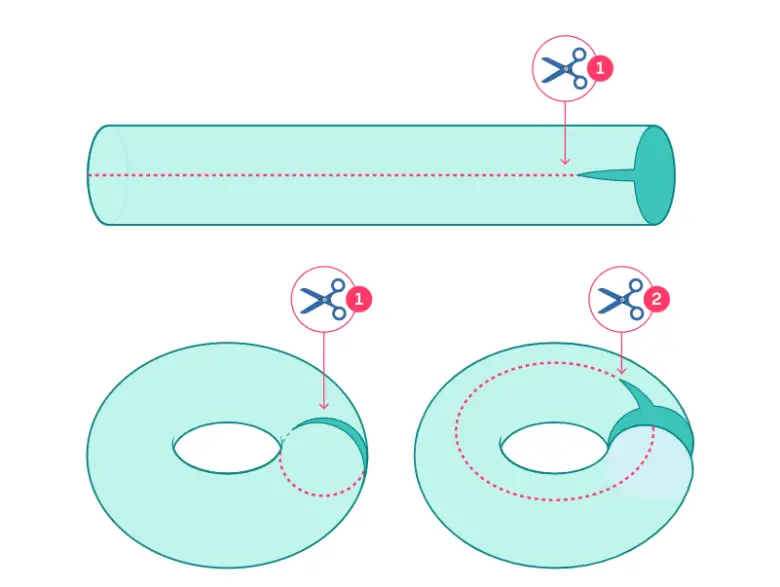
Matematikçi Bernhard Riemann’a göre, bir nesnedeki deliklerin sayısı, o nesnenin iki ayrı parça oluşturmadan kaç kez kesilebileceği ile tanımlanır. Bu tanıma göre, bir pipet yalnızca bir kez – uçtan uca – kesilebildiği için, tam olarak bir deliği vardır.
Buna karşılık, bir torus (veya bildiğimiz adıyla simit) iki farklı şekilde kesilebilir. İlk kesim, torusun ortasındaki delikten bir çember boyunca yapılabilir. İkinci kesim ise, torusun dışını çevreleyen ve bir daire oluşturan yol boyunca gerçekleştirilebilir. Bu özellik, simidin iki deliğe sahip olduğunu gösterir.
Tüm bu fikirlerden yola çıkarak, günümüzde topolojide deliklerin sayısını tanımlamak için Henri Poincaré tarafından tanıtılan Betti sayıları kullanılmaktadır. Betti sayıları, bir nesnenin yüzeyindeki deliklerin sayısını ve türlerini matematiksel olarak ifade eden bir araçtır.
Ancak hangi yöntemi kullanırsanız kullanın, bir pipetin matematiksel açıdan yalnızca bir deliği olduğu sonucuna ulaşırsınız. Bu, topolojik tanımlamaların günlük delik kavramından nasıl farklılaştığını bir kez daha gözler önüne serer.
Kaynaklar ve ileri okumalar
- Topology 101: The Hole Truth; Yayınlanma tarihi: 26 Ocak 2021; Bağlantı: Topology 101: The Hole Truth/
- Betti Number; Bağlantı: https://mathworld.wolfram.com/
- What We Talk about When We Talk about Holes; yayınlanma tarihi: 25 Aralık 2014; Bağlantı: https://blogs.scientificamerican.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel