Matematiksel düşünme biçimi ile bir problem nasıl çözülür? Karşılaşılan problemlerde izlenecek özel bir yol var mıdır? Varsa nedir? Bu soruya “Evet” yanıtını 1940’lı yılların ortasında Macar bir matematikçi George Polya verdi. Kendisi 1945’te onun herkes tarafından bilinirliğini arttıran ve günümüze kadar etkisini sürdüren How to Solve It (Nasıl Çözmeli?) isimli kitabını yazdı.
Problem çözme aşamalarını anlattığı bu kitabın belki de en çarpıcı cümlesi “Eğer bir problemi çözemiyorsanız onun resmini çizin.” idi. Kendisinin ortaya koyduğu ve temelinde sadece matematik problemlerini değil, hayatta karşımıza çıkan her türlü problemi çözmek için kullanabileceğimiz bu 4 aşamalı algoritmanın detaylarına geçmeden önce kısaca George Polya’yı tanıyalım.
George Polya Kimdir?
George Pólya matematik eğitimi, problem çözme ve düşünme becerilerine odaklanan çalışmaları ile tanınır. Pólya’nın en ünlü eserlerinden biri, “How to Solve It” adlı kitaptır. Kitap, problem çözme sürecini açıklar, analitik düşünmeyi teşvik eder ve bir problemi adım adım nasıl yaklaşılacağını öğretir.
Bir matematikçi olarak Pólya, sezgisel yöntemler veya problemlerin nasıl çözüleceği çalışması da dahil olmak üzere çok çeşitli problemler üzerinde çalıştı. Kitabı okuduğunuzda, Pólya’nın zihninde rehberli bir tura çıkıyormuşsunuz gibi hissersiniz. Bunun nedeni, yazılarının meta-bilişsel olmasıdır; yani düşünme hakkında nasıl düşündüğünü yazar. Ve meta-biliş genellikle problem çözmenin kalbidir.
George Polya’nın 4 Aşamalı Problem Çözme Algoritması
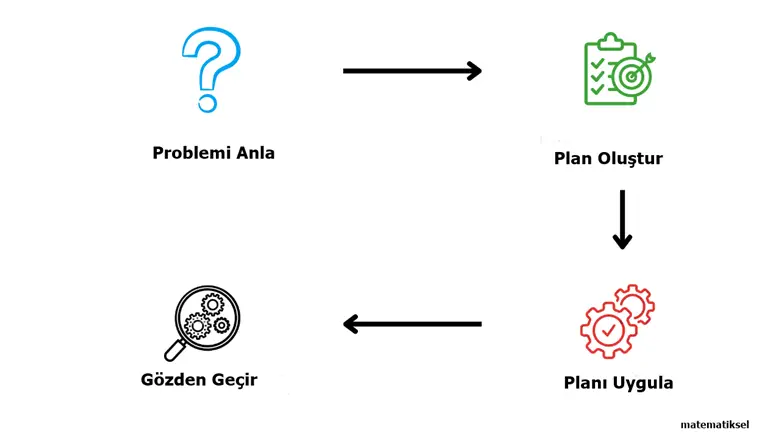
1. Adım: Problemi Anla
Problemi anlamak zorundasınız. Öncelikle problem durumunun açık bir şekilde konulması gerekir. Kendinize ve ya öğrencinize şu soruları sormalısınız;
- Bilinmeyen şey nedir? Veriler nedir? Koşullar nelerdir? Sizden istenen nedir?
- Koşullar yeterli mi? Veriler bilinmeyeni açıklamak için yeterli mi? Verilerde çelişki ya da düzensizlik var mı?
- Bu durumda sizden çözmeniz beklenen durum ya da problem tam olarak nedir ? Neyi bulmanız ya da çözmeniz beklenmektedir?
- Problemi kendi cümlelerinizle ifade edin.
- Problem durumunun bir resmini ya da şemasını çizerek (yapabiliyorsanız) meseleyi daha açık hale getirin
2. Adım: Plan Oluştur
Problem durumunu ortaya koyduk. Neyle karşı karşıya olduğumuzu biliyoruz. Şimdi problemi nasıl çözeceğimize odaklanmalıyız. Polya burada bazı temel problem çözme metotlarından bahsediyor. Ama bu metotlardan birini seçmeden önce kendimize -ya da öğrencimize- sormamız gereken sorular var.
- Bu tipte bir problemle daha önce karşılaştın mı? Bu probleme benzer ve ya bu problemi hatırlatan problemlerle karşılaştın mı? Orada ne yapmıştın onu hatırla.
- Bu problemle bağlantılı olabilecek tarzda bir problem biliyor musun? Kullanışlı olabilecek kurallar ya da teoremler biliyor musun? Listele.
- Bu problemi çözemiyorsan, buna benzer daha basit bir problem ifade edip çözebilir misin?
- Tasarladığın çözümde tüm verileri ve mevcut koşulları kullanabiliyor musun?
Bu temel sorulara yanıt verdikten sonra çözüm hakkında bir fikre sahip olmalıyız. Çözüm için aşağıdaki metotların birini ve ya birkaçını kim bilir belki hepsini kullanabiliriz:
- Sistematik bir liste yapın.
- Sondan başa doğru gidin.
- Baştan sona doğru gidin.
- Bir örüntü arayın.
- Koşulları daraltın.
- Koşulları gevşetin.
- Bir zıt örnek arayın
- İhtimalleri eleyin
- Bir tahminde bulunun ve deneyin.
- Bölün ve parçalar halinde çözün.
- Modelleri, teoremleri ve ya kuralları kullanın.
- Denklem haline getirip çözün.
3. Adım: Planı Uygula
Bu adım plan yapmaktan daha basit. Yapmamız gereken tek şey planımızı uygulamak. Genellikle ihtiyaç duyulan tek şey dikkatli ve sabırlı bir şekilde çözüm stratejimizi uygulamak olacaktır. Stratejinin işe yaramıyor olması bizim hatamızdan kaynaklanıyor olması mümkündür. Bu noktada gerekli ısrarı göstermekten çekinmeyin. Sezgilerinize güvenin. Yine de çözüm olmaması durumunda 2. adıma dönerek stratejiyi değiştirme yoluna gidilmelidir.
4. Adım: Gözden Geçir
Bu aşamada sonucun doğruluğu incelenmelidir. Kullanılan stratejinin uygunluğu ve alternatif çözüm yolları değerlendirilir. Ayrıca Polya bu değerlendirmenin aşağıdaki temel soruları sorarak yapılması gerektiğini belirtiyor.
- Sonucun doğruluğunu sağlayabiliyor musun?
- Tüm verileri kullandın mı?
- Sonucun istenilen koşulları sağlıyor mu?
- Problem farklı bir yolla çözülebilir miydi?
- Elde ettiğin sonuç ve ya kullandığın metot farklı problemlerde kullanılabilir mi?
George Polya, 17 dile çevrilen bu önemli eserinde bir matematikçinin problem çözümü için kat ettiği adımları “her seviyede kullanıcı” için özetlemiştir. Daha da önemlisi Polya öğrencilere problem çözme işinin (ki bu işi yaşamımız boyunca yapıyoruz) öğretilmesi için tüm öğretmenlere eşi bulunmaz bir destek sunmuştur.
Kaynaklar ve ileri okumalar
- Boaler, Jo & Chen, Lang & Williams, Cathy & Cordero, Montserrat. (2016). Seeing as Understanding: The Importance of Visual Mathematics for our Brain and Learning. Journal of Applied & Computational Mathematics. 05. 10.4172/2168-9679.1000325.
- These four easy steps can make you a math whiz. Yayınlanma tarihi: 12 Temmuz 2017. Kaynak site: Conversation. Bağlantı: These four easy steps can make you a math whiz
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak, bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel
