Sir Arthur Conan Doyle’un yarattığı kurgu karakter Sherlock Holmes, dünyanın en iyi dedektifi olarak kabul edilir. Çoğu polis dedektifi olayları çözerken tümdengelimli (deductive) akıl yürütme yöntemini kullanır. Sherlock Holmes ise bunun tersine, tümevarım (inductive) yönteminde ustalaşmıştır. Peki, bu iki yöntem arasındaki fark tam olarak nedir?

Matematikte de gerçeklere deneyle, gözlemle değil, çoğu zaman akıl yürütmeyle ulaşılır. Bu nedenle akıl yürütmenin öğrenilmesi yalnız matematik eğitiminde değil, eğitimin her alanında vazgeçilemez bir gereksinimdir. Şimdi detaylar.
Tümdengelim (Deductive Reasoning) Nedir?
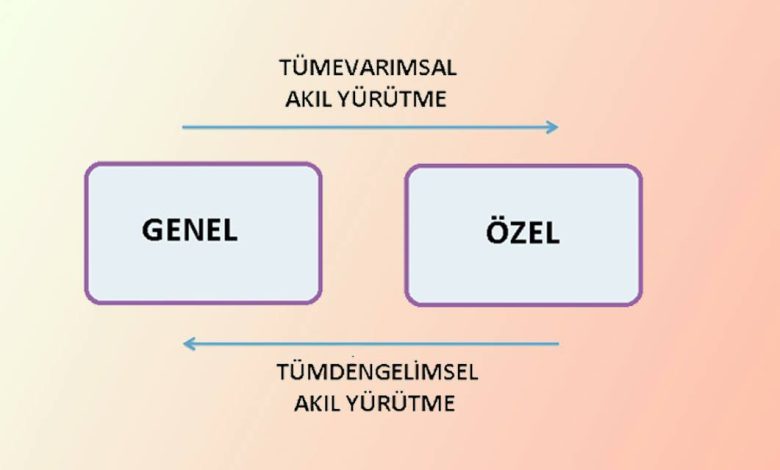
Tümdengelim, genel kabul görmüş öncüllerden yola çıkarak kesin sonuçlara ulaşma yöntemidir. Eğer başlangıçtaki önermeler doğruysa, varılan sonuç da zorunlu olarak doğru kabul edilir. Bu yüzden tümdengelim, “yukarıdan aşağıya” işleyen bir akıl yürütme biçimi olarak tanımlanır.
Tümdengelim genellikle şöyle işler: İlk olarak genel bir yargı ortaya konur. Ardından bu yargıyla ilişkili ikinci bir önerme yapılır. Her iki önerme doğru kabul edildiğinde, bu iki ifade arasında kurulan bağlantı mantıklı bir sonuca ulaşılmasını sağlar. Bu yapıya mantıkta “kıyas” (syllogism) adı verilir.
Bu tür akıl yürütme, günlük yaşamda da sıkça kullanılır. Ancak en sistematik biçimde bilimsel araştırmalarda karşımıza çıkar. Bilimsel yöntemlerin temelinde, hipotezlerin doğruluğunu test etmek için tümdengelim yer alır.
Örnekler:
- Önerme A: Bütün insanlar ölümlüdür.
- Önerme B: Sokrates bir insandır.
- Sonuç: Sokrates ölümlüdür.
- Önerme A: Tüm memelilerin omurgası vardır.
- Önerme B: Köpekler memelidir.
- Sonuç: Köpeklerin omurgası vardır.
- Önerme A: Zıt yüklü parçacıklar birbirini çeker.
- Önerme B: Bu iki molekül birbirini itiyor.
- Sonuç: Moleküller ya her ikisi de pozitif ya da her ikisi de negatif yüklüdür.
Tümdengelim, mantıklı ve kesin sonuçlara ulaşmanın güçlü bir yoludur. Ancak bu yöntem, yalnızca öncüller doğruysa güvenilir sonuçlar üretir.
Tümevarım (Inductive Reasoning) Nedir?
Tümevarım, tümdengelimin tersine işler. Burada, belirli gözlemlerden veya örneklerden yola çıkarak genel bir sonuca ulaşılır. Yani küçük verilerden hareketle daha kapsayıcı bir yargı ortaya konur.
Bu nedenle tümevarım, genellikle sınırlı verilerle hipotez oluşturmak için kullanılır. Mevcut bir hipotezi desteklemekten çok, yeni bir fikir geliştirmek amacı taşır. Ancak bu yöntemde ulaşılan sonuçlar, tümdengelime göre daha düşük kesinlik taşır. Çünkü başlangıçta doğru olan gözlemler, genelleme yapıldığında her zaman geçerli olmaz.
Örnekler:
- Ne zaman soğuk algınlığı geçirsem, çevremdekiler de hasta oluyor. O halde soğuk algınlığı bulaşıcıdır.
- Torbadan çekilen ilk bilye siyahtı. İkincisi ve üçüncüsü de siyah. O halde torbadaki tüm bilyeler siyahtır.
- Karşılaştığım her kedi tüylüydü. Demek ki bütün kediler tüylüdür.
- Karşılaştığım her köpek arkadaş canlısı. Demek ki köpekler genellikle arkadaş canlısıdır.

Bilimde ne tümdengelim ne de tümevarım mutlaka birbirine üstün değildir. Bunun yerine, gözlemlere mi yoksa teoriye mi dayalı tahminlerde bulunduğumuza bağlı olarak ikisi arasında sürekli bir etkileşim vardır.
Hangisi Daha İyi?
Tümdengelim, genelden özele ilerleyen bir akıl yürütme biçimidir. Önermeler doğruysa, sonuç da zorunlu olarak doğrudur. Tümevarım ise tam tersini yapar: belirli gözlemleri kullanarak genel bir sonuca ulaşmaya çalışır. Bu yüzden tümevarım, genellikle yeni bir hipotez oluştururken işe yarar. Ancak her gözlem genellenemez, bu nedenle sonuç her zaman kesin olmaz.
Tümdengelimi kullanan biri, “Bu genelleme doğruysa, o zaman bu özel durum da doğrudur” der. Tümevarımı tercih eden biri ise “Bu örnekler böyleyse, genel kural da böyle olabilir” sonucuna varır. Tümdengelim ya çalışır ya çalışmaz; gri alan yoktur. Oysa tümevarım, güçlüden zayıfa doğru birçok olasılık içerir.
Bilim insanları her iki yöntemi bir arada kullanır. Bazen teoriyle başlar, gözlemle test eder. Bazen gözlem yapar, örüntüleri fark eder ve oradan bir hipotez geliştirir. Bilim, bu iki yöntemi dengeleyerek ilerler. Ne biri diğerinden üstündür, ne de biri yeterlidir. Bilgiye ancak bu karşılıklı etkileşimle yaklaşabiliriz.
Kesin bilgiye ulaşamayız ama bilim, elimizdeki en sağlam yaklaşım aracını sunar. Yine de, bu yöntemlerin kusursuz olduğunu söyleyemeyiz. Tümdengelime dayanan biri, yanlış bir öncül kullanırsa bütünüyle hatalı bir sonuca varır. Tümevarıma güvenen biri ise yetersiz veriyle zayıf bir genelleme yapar.
Bu farkları göstermek için felsefeci Diyojen’in meşhur örneği ilginç bir ders sunar. Platon, hocası Sokrates’in tanımını aktarırken “İnsan, tüysüz iki ayaklı bir canlıdır” der. Diyojen, bir tavuğu yolup salona getirir ve “İşte size bir insan!” diyerek alay eder. Bu örnek, tümdengelimin ne kadar kolay boşa düşebileceğini gösterir. Tanım doğru görünse de öncül yanlışsa sonuç da saçma olur.
Öte yandan tümevarım da hata payı taşır. Örneğin: “Penguenler kuştur. Penguenler uçamaz. Öyleyse tüm kuşlar uçamaz.” Bu çıkarım da veriler yetersiz olduğu için yanlıştır. Tümevarım ancak güçlü ve çeşitli gözlemlerle doğru sonuçlara yaklaşır.
Sonuç olarak, tümdengelim de tümevarım da bilimsel düşüncenin temel araçlarıdır. Her biri kendi sınırları içinde anlamlıdır. Ama yanlış kullanıldığında, ciddi hatalara da yol açar.
Tümevarım ve Tümdengelimin Ötesinde: Tümleme Akıl Yürütme (Abductive Reasoning)
Günlük yaşantımızda en sık kullandığımız akıl yürütme biçimlerinden biri aslında ne tümdengelimdir ne de tümevarım. Tümleme (abductive) akıl yürütme, sınırlı bilgiye dayanarak en olası açıklamayı tahmin etme sürecidir. Bu nedenle çoğu zaman “en iyi açıklamaya ulaşma yöntemi” olarak tanımlanır.
Tümleme, tümdengelimin yapısal kesinliğiyle tümevarımın gözlemsel yönünü birleştirir. Ancak burada sonuç kesin değildir; sadece mevcut veriler ışığında en makul olan seçilir.
Bir kadın bir masada otururken önünde iki kadeh şarap duruyorsa ve yalnızsa, onunla birlikte olan kişinin kısa süreliğine uzaklaştığını düşünebiliriz. Bir dükkânın önünde tasmalı bir köpek bağlıysa, sahibinin alışverişte olduğunu varsayarız. Elimizde kesin bilgi yoktur ama bağlam, bu sonuçları en olası hale getirir.
Bu yöntemde ana önerme açıktır; ancak ikincil önerme ve sonuç yalnızca olasılıksaldır. Veriler doğruysa sonuç da doğru olma eğilimindedir ama hiçbir zaman garantili değildir. Yine de, bu mantık türü hem gündelik akıl yürütmede hem de bilimsel hipotez geliştirme süreçlerinde oldukça kullanışlıdır.
Sherlock Holmes ve Tümleme Akıl Yürütme
Sherlock Holmes yalnızca tümevarım ustası değildir; aynı zamanda güçlü bir tümleyici akıl yürütme yeteneğine sahiptir. Conan Doyle’un The Adventure of the Dancing Men öyküsündeki bir sahne, bunu açık biçimde gösterir.
Holmes, Watson’a Güney Afrika menkul kıymetlerine yatırım yapmayacağını söyler. Watson şaşkınlık içinde nasıl bildiğini sorar. Holmes, ardışık gözlemlerle Watson’ın akşam kulüpte bilardo oynadığını, yanında yalnızca belirli biriyle oynadığını, bu kişinin kendisine daha önce yatırım teklif ettiğini ve Watson’ın hâlâ çek defterini istemediğini söyler. Sonuç: Watson yatırım yapmayı düşünmüyordur.
Bu zincir, yalnızca tek tek gözlemleri birleştiren bir tümevarım örneği değildir. Holmes, mevcut verilerle uyumlu birçok olası açıklamayı düşünür ve içlerinden en makul olanı seçer. Bu, açık biçimde tümleme yöntemidir. Holmes’un ifadesiyle, “Başlangıç noktasıyla sonucu verirseniz ve aradaki bağlantıları gizlerseniz, karşınızdakine şaşırtıcı bir sonuç sunarsınız.”
Sonuç Olarak
Tümleme, belirsizlik altında karar vermemizi sağlar. Ancak bu yöntemde hata payı da yüksektir. Veriler eksikse ya da bağlam yanlış yorumlanırsa, ulaşılan sonuç yanıltıcı olabilir. Yine de günlük hayatta, tıpta, bilimde ve özellikle dedektiflikte en sık başvurulan yöntem budur.
Kaynaklar ve ileri okumalar
- Deductive versus inductive reasoning: what’s the difference. Yaınlanma tarihi: 30 Mayıs 2023. Kaynak site: ZME Science. Bağlantı: Deductive versus inductive reasoning: what’s the difference
Matematiksel