Eşitlik arayışı çok doğal bir insani duygudur ve tarihin büyük itici güçlerinden biri olmuştur. Eşitlik, en önemli sloganlarından biri “Liberte, egalite, fraternite ou la mort” (özgürlük, eşitlik, kardeşlik yahut ölüm) olan, Fransız Devrimi’nin arkasındaki ideallerden biriydi. Bu dürtü olmasa, çok sayıda sanayi grevi, gösteri, devrim olmazdı. Öte yandan eşitsizlik her yerdedir. Tüm eşitsizliklerin en başında da ekonomik eşitsizlik gelir.

Her ülkede zengin ve fakirler farklı oranlarda vardır. Ve kesinlikle her ülkede zenginler fakirlerden çok daha fazlasına sahiptir. Norveç’teki ortalama gelir, Nijerya’daki ortalama gelirin 19 katıdır. Ve Norveç’teki en yoksul %10, Nijerya’daki en zengin %10’un neredeyse iki katı gelir elde etmektedir.
İki kişi arasındaki dağılımı değerlendirmek kolaydır. Ancak daha büyük gruplardaki veya tüm toplumdaki eşitsizlikleri nasıl değerlendirebiliriz? Gelirin ne ölçüde eşitsiz dağıldığını ölçmenin, matematiksel olarak göstermenin çeşitli yöntemleri vardır. Bunların en başında Lorenz eğrisi ve Gini katsayısı gelir.
Daha yakın zamanda, eşitsizliği ölçmek için ekonomistler Alex Cobham ve Andy Sumner tarafından Palma oranları önerilse de biz yine de bu yazımızda en iyi bilinen ölçütlere odaklanalım. Gini katsayısını anlamk için önce Lorenz Eğrisini tanımalısınız.
Lorenz Eğrisi Nedir? Neyi İfade Eder?
Lorenz eğrisi, 1905 yılında Max O. Lorenz adlı Amerikalı bir ekonomist tarafından servet yoğunlaşmasını ölçmeye yönelik bir yöntem olarak tasarlandı. Bu eğri nüfusun yüzdelik dilimlerini, bu yüzdelik dilimde veya altındaki insanların kümülatif gelirine veya zenginliğine karşı grafik olarak gösterir.
Lorenz eğrisine genellikle eğimi 1 olan köşegen eder; bu, gelir veya servet dağılımında mükemmel eşitliği temsil eder. Yani mutlak eşitlik çizgisi biraz da ütopik bir hayali yansıtır. Lorenz eğrisi onun altında yer alır ve gözlemlenen veya tahmin edilen dağılımı gösterir. Bu eğri her zaman köşegenin altında çıkar. Lorenz eğrisi eşitlik çizgisine ne kadar yakınsa eşitsizlik o kadar azdır ve ne kadar uzaksa eşitsizlik o kadar fazla demektir.
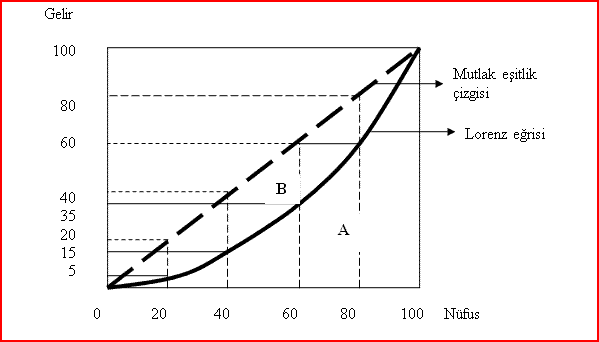
Lorenz eğrisi, bir yüzyıldan fazla bir süredir gelir ve servet dağılımlarını göstermek ve bu dağılımlardaki eşitsizliği incelemek için yaygın olarak kullanılmaktadır. Bu eğri aynı zamanda, eşitsizlik seviyelerinin matematiksel bir temsili olan Gini katsayısının hesaplanmasında merkezi bir parçadır.
Gini Katsayısı Nedir? Neyi İfade Eder?
İtalyan istatistikçi Corrado Gini tarafından 1912’de geliştirilen Gini endeksi veya Gini katsayısı, , hanelerden ülkelere kadar hem küçük hem de büyük nüfuslar için geçerli olan bir gelir eşitsizliği ölçüsüdür. Gini katsayısı sıfırdan bire kadar bir ölçekte ölçülür. Herkesin geliri aynı ise gelir eşitsizliği olmadığı için Gini katsayısı 0 değerini alır. Tek bir birey tüm geliri alıyorsa Gini katsayısı maksimum 1 olacaktır. Ancak Gini katsayısının sıfır olması mutlaka iyi değildir, çünkü gruptaki herkes eşit derecede fakir veya muhtaç olabilir.
Bir Lorenz eğrisinin altında yatan veriler, eşitsizliği matematiksel olarak ölçmenin birincil yolu olan Gini katsayısını hesaplamak için gereklidir. Yukarıdaki grafikte, Lorenz eğrisi ile mutlak eşitlik çizgisi arasında bir boşluk olduğunu görebilirsiniz. Gini katsayısı bu alanın 45 derecelik çizginin altındaki üçgenin tamamının alanına oranı olarak hesaplanır. Yani Gini katsayısı = B / (A + B) biçimindedir.
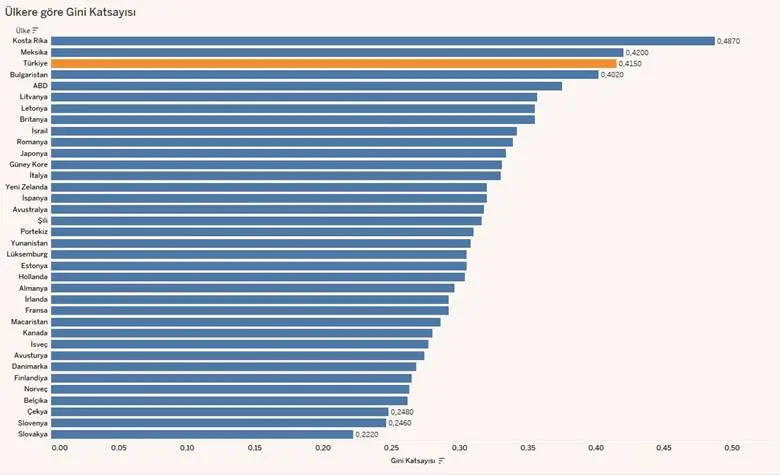
Gini katsayısı gibi birçok eşitsizlik rakamı ülkeler için tek tek hesaplanır. Bununla beraber, küreselleşme nedeniyle ulusal ekonomilerin entegrasyonunun artmasıyla birlikte, insanlar bir bütün olarak, dünyadaki gelir dağılımındaki değişikliklerle daha çok ilgilenir olmuşlardır. Bu nedenle küresel Gini katsayısı olarak bilinen bir başka hesaplama daha vardır. Bu katsayı dünyadaki her bir bireyi aynı ülkenin vatandaşlarıymış gibi ele alarak hesaplanır.
Dünyanın en fakir ülkelerinden bazıları dünyanın en yüksek Gini katsayılarından bazılarına sahipken, en düşük Gini katsayılarının çoğu daha zengin Avrupa ülkelerinde bulunmaktadır. Gerçek yaşamda ise hiçbir ülkenin Gini katsayısı 0,2’nin altında ve 0,75’in üzerinde değildir.
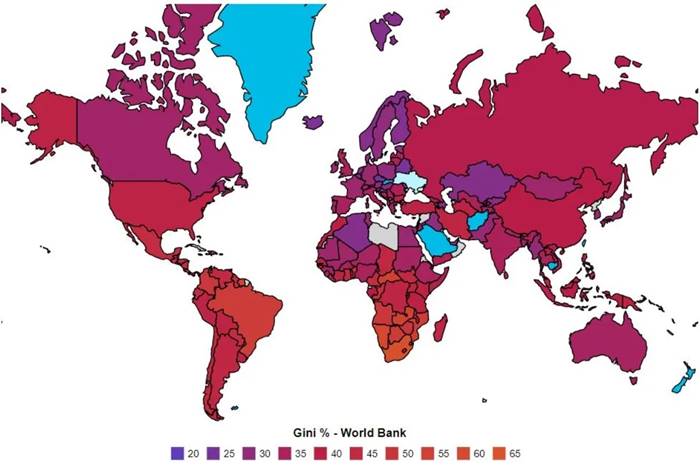
Avrupa kıtasında Gini katsayıları 0,2 ile 0,3 arasındadır. Bunların birçoğu güçlü bir refah devletine sahip olan kapitalist ülkelerdir. Diğer uçta ise Gini katsayıları 0,6’nın üzerinde olan ülkeler yer alır. Bunların hepsi Güney Afrika’da bulunur. Diğer birçok ülkede ise Gini katsayıları 0,3 ile 0,5 arasında dağılmıştır.
Sonuç Olarak;
Şu ana kadar sizlere aktardıklarımız, gelir dağılımı eşitsizliğinin matematiksel olarak nasıl hesaplandığını göstermek amacını taşıyordu. Ancak elbette bunlar sadece işin analiz kısmı. Aslında şu bildiğimiz cümle, gelir dağılımı çarpıklığını kısa ve öz şekilde anlatmaya yetiyor. ”Dünyanın en zengin yüzde 1’lik kesiminin serveti, geri kalan yüzde 99’luk kesimin servetinin toplamına eşit.”
Kaynaklar ve ileri okumalar:
- Gini Index Explained and Gini Co-efficients Around the World. kaynak site: Investopia. Yayınlanma tarihi: 21 Şubat 2024.; Bağlantı: Gini Index Explained and Gini Coefficients Around the World
- Sitthiyot, T., Holasut, K. A simple method for measuring inequality. Palgrave Commun 6, 112 (2020). https://doi.org/10.1057/s41599-020-0484-6
- Sitthiyot, T., Holasut, K. A simple method for estimating the Lorenz curve. Humanit Soc Sci Commun 8, 268 (2021). https://doi.org/10.1057/s41599-021-00948-x
- What factors influence income inequality?. Yayınlanma tarihi: 21 Temmuz 2016. Kaynak site: Conversation. Bağlantı: What factors influence income inequality?
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










