Elinizi ateşe yaklaştırırsanız elleriniz yanacaktır. Benzer bir biçimde kara dokunduğunuz zamanda da parmaklarınız üşüyecektir. Sonucunda vücudumuz sıcaklık değişimlerini kolayca algılar. Peki ama çok basit bir soru soralım. Sıcaklık tam olarak nedir?

Eğer temel lise eğitimi aldıysanız bu sorunun cevabını vermeniz oldukça kolay olacaktır. Sonucunda bildiğiniz gibi sıcaklık bir malzemeyi oluşturan atomların ve moleküllerin hareketine bağlıdır. Sıcaklık, tüm bu atomların ve moleküllerin ortalama kinetik enerjisi ile orantılıdır.
Bu bize iki şey söylüyor. Birincisi, bir ortalama olduğu için, sıcaklık istatistiksel bir niceliktir. Yani atomların ya da moleküllerin toplu biçimde davranması ile ilgilidir. İkincisi, makroskobik bir niceliktir. Yani tek tek ele aldığınız zaman atomların ve moleküllerin bir sıcaklığı yoktur. Sıcaklık bu mikroskobik bileşenlerin kolektif davranışından ortaya çıkar. Benzer bir durum basınç tanımı için de geçerlidir.
İstatistiksel Mekanik Nedir?
İstatistiksel mekanik, sıcaklık ve basınç gibi kavramları açıklamak için mikroskobik ve makroskopik arasındaki istatistiksel ilişkiyi kesinleştirir. Fizikte mikro durum, sistemdeki her molekülün tek bir anda düzenlenmesi olarak tanımlanır. Makro durum ise, sıcaklık, basınç ve hacim gibi sistemin makroskobik özellikleri ile tanımlanır.

Örnek olarak bir kutu içinde bir gaz düşünün. Herhangi bir zamanda bu sistem, sıcaklık, basınç ve gazın hacmi gibi ölçebildiğimiz makroskobik niceliklerle tanımlanan belirli bir makrodurumdadır. Aynı zamanda bu sistemde, gazı oluşturan moleküllerin konumları ve momentumları tarafından tanımlanan belirli bir mikrodurumdadır.
Mikro durumu değiştirmek – örneğin birkaç molekülü değiştirmek – makro durumda mutlaka bir fark yaratmayacaktır. Başka bir deyişle, her makrodurum, bir dizi (muhtemelen çok sayıda) farklı mikroduruma karşılık gelir.
Belirli bir makro durum göz önüne alındığında, gazın hangi mikro durumda olduğunu söylemenin hiçbir yolu yoktur. Temelinde bunu ölçmek imkansızdır. Ancak, sistemin doğası hakkında bazı varsayımlarda bulunmak mümkündür. Bu elbette matematik sayesinde olacaktır. Maxwell-Boltzmann dağılımı tam da bunu yapan bir olasılık dağılımı örneğidir.
Maxwell-Boltzmann Dağılımı Nedir?
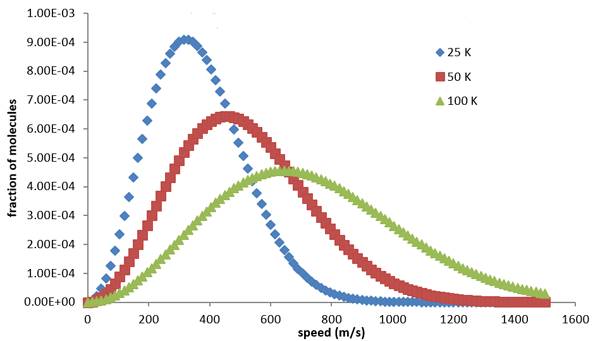
Bir kutunun içindeki gazın termal dengede olduğunu yani ısı alış verişinin sıfır olduğunu varsayarsak bu dağılım size rastgele bir molekülün veya atomun belirli bir hızda hareket etme olasılığını söyler. Dağılımın ortaya koyacağı sonuçlar gazın sıcaklığına ve moleküllerin kütlesine bağlıdır. Aşağıda, çeşitli sıcaklıklarda hidrojen atomlarının dağılımının grafikleri bulunmaktadır.
Grafikte daha yüksek sıcaklıklar için daha yüksek hızların daha olası olduğunu görebilirsiniz. ( Olasılık dağılımları, önceden emin olamayacağınız birden fazla sonucu olan süreçleri tanımlamamıza yarar. Konu hakkında temel bilgileri bu yazıda bulabilirsiniz: Temel İstatistik Kavramları: Bilmeniz Gereken Bazı Olasılık Dağılımları )
Gazların kinetik teorisi, gazı oluşturan moleküler parçacıkların hareketi olarak bir gazın fiziksel davranışını açıklayan bilimsel bir modeldir. Bu modelde, gazı oluşturan parçacıklar (atomlar veya moleküller) yukarıda da belirttiğimiz gibi sürekli olarak rastgele hareket eder ve bu süreçte hem birbirleriyle hem de gazın içinde bulunduğu herhangi bir kabın kenarlarıyla çarpışır. Gazın ısı ve basınç gibi fiziksel özelliklerine yol açan bu harekettir.
Dağılım, adını 19. yüzyılda gazların kinetik teorisini geliştirmede önemli adımlar atan James Clerk Maxwell (1831 -1879) ve Ludwig Boltzmann’dan (1844 -1906) almıştır. İstatistiksel mekaniğinin gelişimine katkıda bulunan diğer bir önemli isim ise Josiah Willard Gibbs idi. İstatistik mekaniğinin matematiksel yapısı, onun tarafından kaleme alınan Elementary Principles in Statistical Mechanics (1902) adlı kitabıyla şekillenmişti. İlgili hesaplamalara bu yazıda girmeyeceğiz. Ancak erişmek isterseniz bu kaynağa göz atabilirsiniz:
İstatistiksel Mekanik Ne İşe Yarar?
İstatistiksel Mekanik, kuantum teorisi ve görelilik teorisinin yanında modern fiziğin üçüncü ayağıdır. Amacı, fiziksel sistemlerin makroskopik davranışını, bu sistemlerin mikroskobik bileşenlerini yöneten dinamik yasalar ve olasılıksal varsayımlar açısından açıklamaktır.
Yukarıda da değindiğimiz gibi çok sayıda parçacıktan oluşan mikroskobik sistemlerin davranışını incelemek adına istatistiğe ihtiyaç duyarız. Başlangıçta gazlar gibi fiziksel sistemleri tanımlamak için geliştirilmiş olmasına rağmen, istatistiksel mekanik artık günümüzde çok farklı alanlarda uygulamalara sahiptir. İnsanların, trafiğin veya biyolojik hücrelerin davranışlarını modellemek için de kullanılmaktadır.
Son olarak, entropi kavramından söz edilmeden istatistiksel mekanikle ilgili hiçbir açıklama tamamlanmış sayılmaz. Entropiyi yorumlamanın bir yolu, bir gaz kutusu gibi bir sistemdeki düzensizlik miktarının bir ölçüsüdür.
Günlük hayattan bir örnek verirsek, tamamen dolu bir pilin entropisi düşük olur; pil boşaldıkça entropi artar. Kurmalı bir oyuncak kuruluyken entropisi düşüktür; yayı boşaldıkça entropisi artar. Tamamen boşaldığın da, kendimiz enerji harcayarak tekrar kurarız. Bu sayede entropisini tekrar eski düşük seviyesine getiririz.
Termodinamiğin ikinci yasasına göre, dışarıdan enerji verilmediği sürece entropi hep artar, hiç azalmaz. Oyuncağın entropisi azalır fakat biz onu kurarak “iş yaparız”. Bunun sonucunda, bizim entropimizdeki artış miktarı, oyuncağın entropisindeki düşüş miktarını karşılar.
Bir cismin entropisi ile makroskobik durumunun olasılığı arasındaki kesin bağlantı, günümüzde Viyana mezarlığındaki mezarına kazınmış durumdadır. Burada S entropi, W söz konusu olasılık ve k ise onuruna Boltzmann sabiti olarak bilinir. ( Kendisi hakkında daha kapsamlı bilgiyi bu yazıdan edinmeniz mümkün: Düzensizliğin Dahisi: Ludwig Boltzmann)
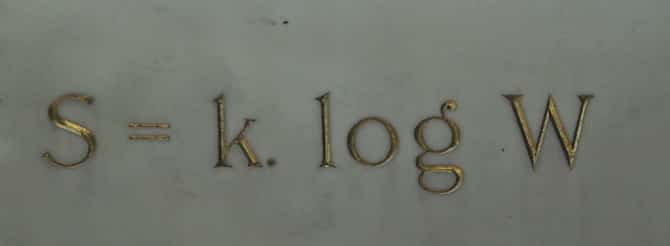
Entropiyi ifade eden geleneksel matematiksel sembol S’dir. Hem bu hem de adı, konu üzerine detaylı çalışmalar yapan Alman matematikçi ve fizikçi Rudolf Clausius’a (1822-1888) tarafından tanımlanmıştır. Entropide olan değişiklik ΔS biçiminde gösterilirse Termodinamiğin İkinci Yasasının kısa ve öz bir temsili şu şekilde olur: ΔS ≥ 0. Daha fazla bilgi için de bu yazıya bakabilirsiniz. Entropi Nedir? Termodinamiğin İkinci Yasası Tam Olarak Ne Anlama Geliyor?
Kaynaklar ve ileri okumalar
- Maths in a minute: Statistical mechanics. Yayınlanma tarihi: 12 Şubat 2022; Bağlantı: https://plus.maths.org/
- Philosophy of Statistical Mechanics. yayınlanma tarihi: 1o Ocak 2023; Bağlantı: https://plato.stanford.edu/entries/statphys-statmech/
- Makro Durumlar ve Mikro Durumlar. Bağlantı: https://tr.khanacademy.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel