Galton Kutusu Kullanarak Geleceği Nasıl Görebilirsiniz?

Geleceği görmek birçok zaman fantezi ve bilim kurgu malzemesidir. Ancak aslında geleceği görmek için kristal bir küreye veya kahve fallarına ihtiyacınız yok. Size tek gereken matematiktir.

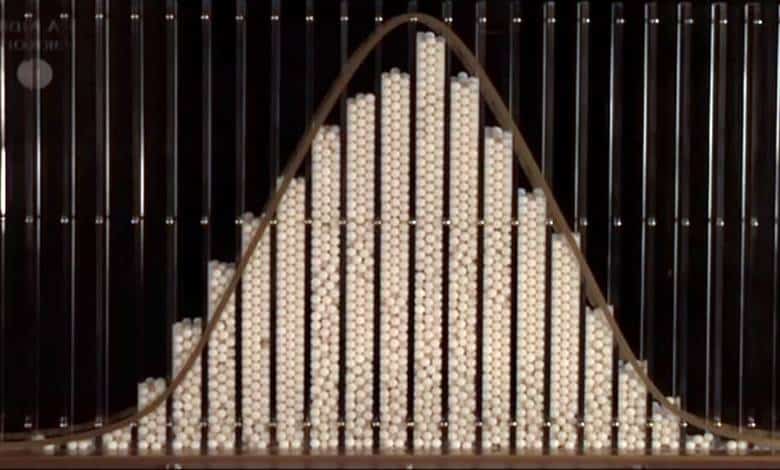
Dünya bazen rastgele veya öngörülemeyen olaylarla yönetiliyor gibi görünse de, matematiksel olasılık ve istatistik alanları birçok gerçekliğin şaşırtıcı bir doğrulukla tahmin edilebileceğini bizlere göstermiştir. 19. yüzyıl İngiliz istatistikçisi Sir Francis Galton da tasarladığı Galton tahtası / kutusu aracılığı ile aslında bize geleceği göstermeye çalışıyordu.

Galton Kutusu Nedir?

Sir Francis Galton (1822-1911) tarafından icat edilen Galton kutusu, üstüne üçgen biçimi oluşturacak biçimde çivilenmiş birçok pim barındıran dik bir tahtadır. Tahtanın tepesinde bir kabın içinde, serbest bırakılmaya ve yerçekimi kuvvetine maruz kalmaya hazır toplar yer alır. Pimler birbirine eşit uzaklıkta ve toplar çarpıştığında sağa veya sola düşme şansları eşit olacak şekilde yerleştirilmiştir.

Sonunda toplar serbest bırakılır. Devamında tahtanın dibine bekleme yuvalarından birine düşerler. Her topun sola ya da sağa gitme şansı elbette eşittir. Bu durumda toplar yolculuğunu tamamladıktan sonra ortaya çıkacak olan sonucun ne olacağını tahmin etmek size imkansız gibi gelecektir.

Bununla birlikte, deneyi bir kaç kez tekrar ederseniz aşağı yukarı aynı sonucu göreceğiniz neredeyse kesindir. Matematik yasaları gereği topların çoğu merkezde, az bir kısmı ise kıyılarda toplanacaktır. Merkezden kenara gidildikçe bölmelere giren topların sayısı azalır.

Böylesine doğası gereği rastgele bir süreç nasıl bu kadar tutarlı sonuçlar üretebilir? Sonuçta, her top daha önce gelenlerden tamamen bağımsızdır. Yani dibe ulaşmak için kesinlikle herhangi bir yoldan gitmekte özgürdür.

Bu Nasıl Gerçekleşiyor?

Galton kutusunda karşımıza çıkan bu ilginç durumu anlamanın anahtarı, her bir topu ayrı ayrı düşünmek değildir. Burada tüm top grubunu belirli kurallara göre yönetilen tek bir varlık olarak görmek gerekir.

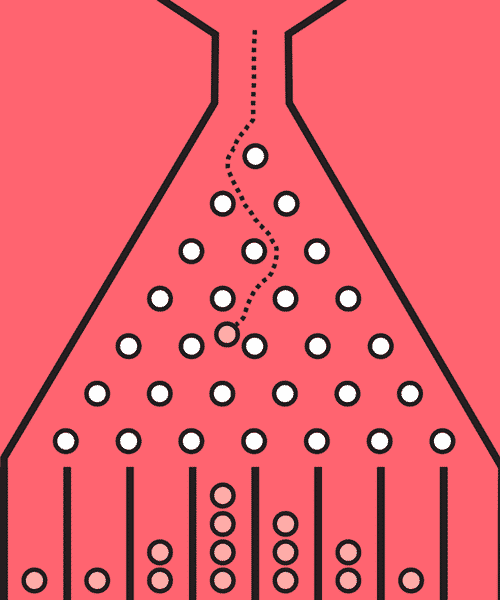
Kalıbı anlamamıza yardımcı olması için, çok daha az iğne içeren bir versiyonu ele alalım. Bu, sorunu yönetebileceğimiz bir ölçeğe indirecektir. Bu sefer ki Galton kutusunda dört sıra pin olsun. Bu durumda, bir topun dibe ulaşması için tam olarak 16 olası yol vardır. Bu olasılıkların her birinin nasıl göründüğünü aşağıda inceleyebilirsiniz.

Tek bir topa odaklanmak yerine tüm potansiyel yolları bir arada görmek, nihai sonucu öngörülebilir kılan şeyin ne olduğunu anlamanıza yardımcı olur. Bu tahtanın tepesinden 160 top bırakırsak, 16 yolun her biri yaklaşık 10 kez kullanılacaktır.

Ancak, birkaç yolun aynı sonuca götürdüğünü fark edebilirsiniz. Örneğin, soldan ikinci yuvaya giden dört farklı yol vardır. Bu, bu yuvaya yaklaşık 40 topun girmesini beklememiz gerektiği anlamına gelir. Aynı şekilde, orta yuvaya götüren altı farklı yol vardır. Bu nedenle toplardan yaklaşık 60 tanesi oraya düşecektir.

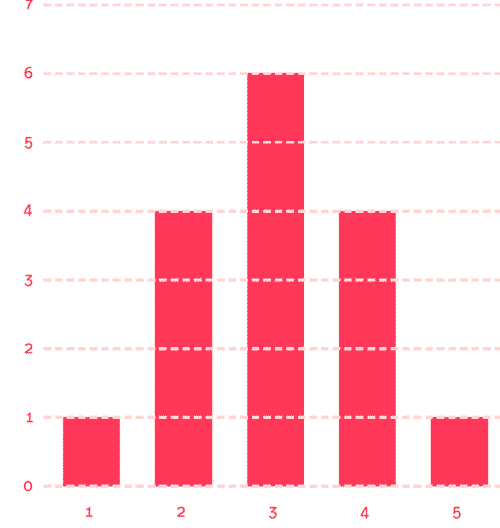
Her yuvaya giden yolların sayısını hesaplarsanız, bu küçük tahta için aşağıdaki sayı serilerini elde edersiniz. Bu 1, 4, 6, 4, 1 biçiminde olur. Bu sayıları bir grafiğe çizerseniz de, görüntüsü aşağıdaki gibi olur.

Bu alıştırmayı daha uzun ve daha fazla yuvaya sahip bir Galton tahtası ile tekrarlayalım. Örneğin 5 yerine 9 yuva seçerseniz şu sayıları elde edersiniz: 1, 8, 28, 56, 70, 56, 28, 8, 1. Bu sefer grafik aşağıdakine benzer.

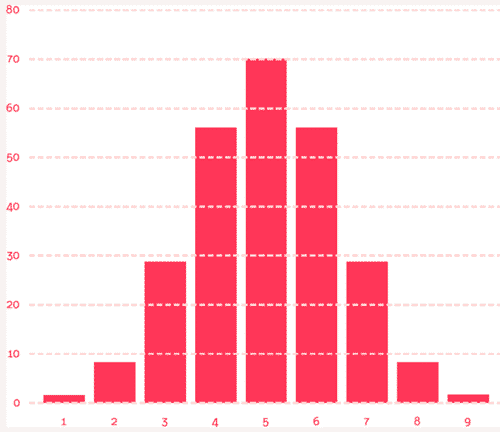
Yukarıda karşımıza çıkan şekli birçok kişi bu şekli çan eğrisi olarak hatırlayacaktır, ancak matematikçiler buna normal dağılım derler. Normal dağılmış herhangi bir niceliğin dağılımının grafiğini çizerseniz, karşınıza çan eğrisine benzer bir şekil çıkar. Toplumda boy uzunluğu, ağırlık, eğitim düzeyi gibi bir çok niteliğin dağılımında bu eğriyle karşılaşırız.

Galton Kutusu Ne İşe Yarar?

Galton Kutusu’nu hayatımıza uyarlarsak, uçlarda yer alan marjinal bireylerin kaderini anlayabiliriz. Marjinaller çan eğrisinin her iki yanında simetrik olarak dağılmışlardır. Örneğin çok kısalar ve çok uzunların sayısı aşağı yukarı birbirine eşittir. Marjinallik, şanslı bir azınlık ile talihsiz bir alt tabakanın payına düşendir.

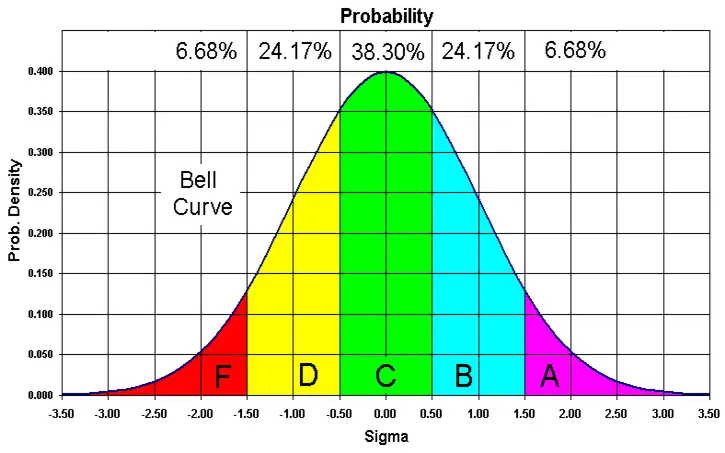
Grup ister insanlardan, ister test puanlarından veya olaylardan olsun, hepsi sonunda bu karakteristik şekli paylaşır. Normal dağılıma götüren ilkeler, birçok günlük olgunun altında iş başındadır. Bu, etkili bir şekilde “geleceği tahmin etmemizi” sağlayan şeydir. Örneğin evinizden şehir merkezine giden bir otobüse biniyorsanız, gideceğiniz yere varmanız ne kadar sürer?

A ve B arasındaki yollarda kapsanan tam mesafeyi belirlemek ve ardından zamanı belirlemek için her yolu hız sınırına bölmek teorik olarak mümkündür. Ancak bu aptalca bir iştir. Yol boyunca durmanıza ve yolculuğunuzu belirsiz sayıda kesintiye uğratmanıza neden olacak trafik ışıkları vardır. Normal dağılım bizi burada kurtaracaktır.

Yolculuktaki trafik ışıkları, iğnelerin bazılarını sola ve bazılarını sağa göndermesi gibi, bazı araçların geçmesine izin verir. Ancak diğerlerini de durdurur. Ve bir yolculukta, Dalton kutusunda sola gitme ihtimalinin çok düşük olduğu gibi, her ışıkta durdurulmanız (veya tersine, bunların hiçbiri tarafından durdurulmamanız) olası değildir.

Gittikçe daha fazla yolculuğa çıktıkça işler değişir. Zamanla yolda harcanan süreniz yukarıdaki topların dağılımı gibi bir biçim oluşturacaktır. Aslında bu verdiğimiz örnek de, çevrimiçi haritaların tipik bir yolculuğun ne kadar süreceğini tahmin etmek için nasıl çalıştığını ve bazen şaşırtıcı derecede doğru olan tahmini varış sürelerini nasıl hesapladığını anlamamız açısından önemlidir.

Yazının devamında göz atmak isterseniz: Abraham de Moivre: Ölüm Tarihini Hesaplayan Bilim İnsanı

Kaynaklar ve ileri okumalar:

• Eddie Woo; It’s a Numberful World: How Math Is Hiding Everywhere; 2019; Isbn: 1615196129
• Galton Board / Quincunx; Bağlantı: https://www.statisticshowto.com
• Galton Board; Bağlantı: https://mathworld.wolfram.com/GaltonBoard.html

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel