Kimyacılar Henry Cavendish’i hidrojenin kaşifi olarak bilir. Biyologlar için onun adı, Cambridge Üniversitesi’ndeki laboratuvarı çağrıştıracaktır. Cavendish Laboratuvarı ise fizikçilerin “dünyayı tartan” adam olarak hatırladıkları kişiye bir saygı duruşu niteliğindedir.

Bilim tarihine damga vurmuş şahsiyetlerin bizden bir farkı vardı. Bir zamanlar bilim günümüzdeki gibi herkese açık değildi. Darwin, Newton, Boyle, Lavoisier gibi isimler elde ettikleri başarılarını varlıklar ve çalışmak zorunda kalmamalarına temelde borçludur. Zenginlikleri ayrıca onlara pahalı laboratuvarı kurma avantajını da vermiştir. Aristokrat bir aileden gelen Henry Cavendish de bunun bir başka örneği idi.
Cavendish ve babası, köklü aristokrat kökenlere sahip bir ailenin üyeleriydi. Babası Lord Charles, eşini Henry’nin küçük kardeşinin doğumunda kaybedince, soyunun geleneksel mesleği olan politikayı terk ederek, oğlu Henry ile paylaştığı ilgi alanı olan bilimi bir hobi olarak takip etmeye başlamıştı. Aile serveti Cavendish’lerin kendi ev laboratuvarlarını inşa etmelerini sağladı. Aristokratik kökenleri onlara bilimsel çevrelere erişme şansını verdi. Bu sayede de Henry Cavendish 27 yaşındayken Royal Society ile tanışacaktı.
Varlıklı bir aileden gelen ve erken yaştan itibaren saygın kabul edilen birinin bir miktar şımarık olmasını da bekleyebilirsiniz. Ancak Henry Cavendish sürekli aynı elbiseleri giyen, yalnız, utangaç ve antisosyal bir karakterdi. Yalnızca geceleri yürüyüşe çıkar ve sadece bilim insanları ile sohbet ederdi. Var olan tek portresi onu profilden gösteriyor çünkü oturarak poz vermeyi reddetmişti. ( Günümüzde kişiliğinin geriye dönük analizi ile kendisinin Asperger sendromuna sahip olduğu düşünülüyor.)

Ancak tüm garipliklerine rağmen Henry Cavendish kendini evreni anlamaya adamıştı. İlgi alanları astronomi, matematik ve fizik idi. Kendisinin adı günümüzde en çok hidrojenin temel yapısını 1766’da keşfetmesiyle hatırlanır. Cavendish, fizikçiler tarafından da dünyayı tartan adam olarak hatırlanmaktadır.
Schiehallion Dağı Deneyi İle Dünya’nın Kütlesi ve Yoğunluğunun Hesaplanması
Newton yerçekimi yasasını 1687’de yayınlamıştı ancak G sabitini veya Dünya’nın kütlesini belirlemeye yönelik herhangi bir girişimde bulunmamıştı. 1700’lü yıllara gelindiğinde gökbilimciler, diğer gezegenlerin yoğunluğunu belirlemeyi mümkün kılacağı için Dünya’nın yoğunluğunu bilmek istiyorlardı. Sonunda Nevil Maskelyne, matematikçi Charles Hutton’ın yardımıyla Schiehallion dağını tartmaya karar verdi. Bunun için kurulan düzenek aşağıdaki gibiydi.
Newton’un yerçekimi yasası aşağıdaki gibidir. Burada Mm, dağın kütlesi ve G, Newton’un Evrensel Yerçekimi Sabitidir. (1). Bu formül aynı zamanda Dünya’nın kütlesi ME ve yarıçapını rE kullanarak da yazılabilir. (2). İkisinin birbirine oranlanması sonucunda da 3 nolu bağlantı ortaya çıkar. Deneyin amacı, Dünya’nın yoğunluğunu ölçekti. Bu durumda kütle yerine yoğunluğun hacimle çarpımını yazarsak da 4 nolu eşitliği elde ederiz.
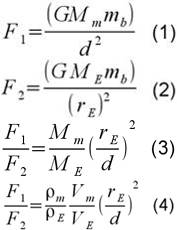
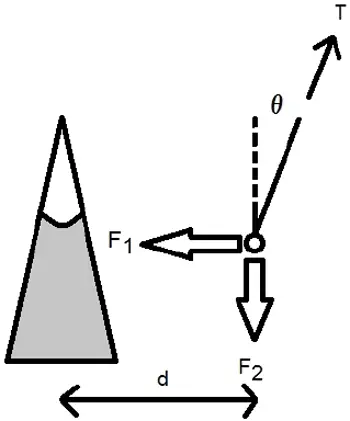
Bu denklemi bir tarafa bırakıp şimdi ipe yoğunlaşalım. İpe etki eden kuvvetleri aşağıdaki gibi gösterebiliriz
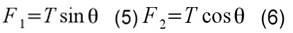
Bu kuvvetleri oranlar ve elde ettiğimiz sonuçları 4 nolu eşitlik ile birleştirsek de durum şu biçimde olur.
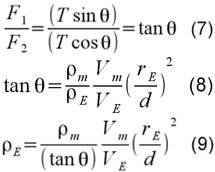
Dünyanın yarıçapı ve hacmini biliyoruz. Dağa kadar olan mesafeyi de ölçmek kolaydır. Dağın yoğunluğu da, yapısındaki kayanın yoğunluğu ile hesaplanır. Ancak, dağın hacmini hesaplamak zordur. Bunun için, Charles Hutton, dağı düzenli aralıklarla yatay dilimlere böldü. Sonrasında her dilimin hacmini hesapladı ve bunları topladı.
Geriye kalan tek değişken sarkaç ipinin sapma açısıydı. Bir Maskelyne, bunun için yıldızları kullanmaya karar verdi. Çalışmaları sonucunda bugün kabul edilen 5.5 gram/cm3 değerinin %75’i olan bir değeri elde ettiler.
Henry Cavendish, Cavendish Deneyi İle Dünyayı Nasıl Tarttı?
Dünyanın yoğunluğu hatalı da olsa bulunmuştu. Buradan da Dünya’nın kütlesi yaklaşık 5.1019 ton olarak ölçüldü. Ancak bu çabalar bilim camiasını memnun etmemişti. Bu durumda sahneye Henry Cavendish çıktı.

Ağırlığınızı ölçmek için isterseniz tartıya çıkarsınız. Bu sayede Dünya’nın yerçekiminin bizi yerde tutmak için ne kadar kuvvetle çektiğini görürsünüz. Gezegenlerin kütlesi de benzer şekilde belirlenir. Bir gökcisminin ağırlığını (daha doğrusu kütlesi) ölçmek için bilim insanları o gezegenin diğer cisimleri nasıl çektiğine bakar. Cismin kütlesi ne kadar fazlaysa uzaydaki diğer cisimlere uyguladığı kütleçekim kuvveti de o kadar fazla olur.
Henry Cavendish sorunu yıllarca düşündü, sonunda 1797’de 67 yaşındayken arkadaşı jeolog John Michell’in kendisine verdiği burulma dengesi aparatıyla işe başladı. Öncelikle Michell’in ekipmanında bazı düzenlemeler yaptı. Sonunda elinde aşağıdakine benzer bir düzenek vardı.
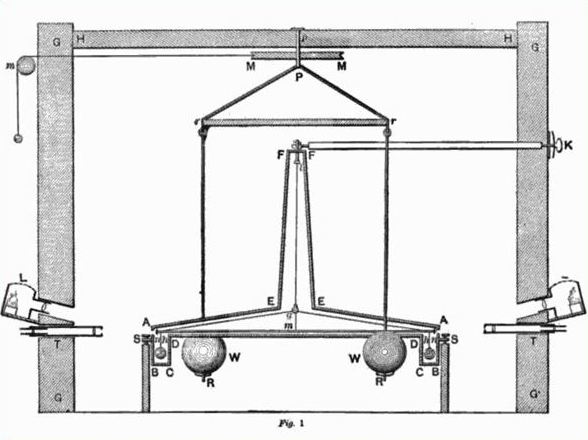
Terazi, iki uçtaki küre biçiminde ağırlıkları taşıyan, yaklaşık bir buçuk metre boyunda ahşap bir çubuktan oluşuyordu. Küre biçimli ağırlıklar ise kuvarstan yapılma bir telle tavandan sarkıyordu. Bu düzenekte bir de ayna vardı. 160 kiloluk iki kurşun küreyi taşıyan bir başka düzenek ise, daha küçük olanın yakınına yerleştirildi.
Deneyde, büyük ve küçük küreler arasındaki kütleçekimi kuvars tele, dönme momenti uyguladı ve telin bükülmesine neden oldu. Cavendish bu bükülmeyi ölçmek için bir ışıktan yararlandı. Aynaya doğrultulan ışık 90 derecelik açıyla yansıdı. Küçük olan büyük olana doğru çekildikçe, dönme hareketi ışık demetinin de hafifçe sapmasına neden oldu.
Cavendish sapmayı dikkatle ölçtü. Sonuçta bu sayede Newton’un, büyük kütlelerin küçük kütleleri çekmesine ilişkin teorisini kanıtlamakla kalmadı aynı zamanda yerkürenin ortalama yoğunluğunu da belirledi. Bu sayede Dünya’nın kütlesinin 5.972 x 1021 ton olduğunu hesapladı.
Sonuç Olarak
Cavendish, bulgularını geliştirmeye devam etti ve nihayet Haziran 1798’de, 57 sayfalık bir makaleyle sonuçlarını bildirdi. Makalesinde Dünyanın yoğunluğunun suyun yoğunluğunun 5,48 katı olduğunu bildirdi. (Şu anda kabul edilen değer 5,52’dir). Daha sonra başkaları da benzer aparatlar kullanarak deneyi tekrarladılar ve neredeyse bir yüzyıl boyunca hiç kimse Cavendish’in orijinal ölçümünün üzerinde bir gelişme elde edemedi.
Bugün Cavendish’in deneyi, Dünya’nın kütlesi ya da yoğunluğunun bir ölçümü olmaktan çok, evrensel yerçekimi sabiti G’yi ölçmenin bir yolu olarak görülüyor. Bugün aynı miktarı ölçmek için son teknoloji ürünü birkaç cihaza sahibiz. Ancak aradan 200 yıl geçmesine rağmen onun ölçümünü çok az geliştirebildik.
Yazımızın devamında bu bilgiyi de öğrenmek isteyebilirsiniz. Everest Dağının Yüksekliği Matematik Yardımı İle Nasıl Ölçüldü?
Kaynaklar ve İleri Okumalar:
- Henry Cavendish, the Eccentric Aristocrat Who Weighed the World. Yayınlanma tarihi: Kaynak site: Bbvaopenmind. Bağlantı: Henry Cavendish, the Eccentric Aristocrat Who Weighed the World
- How do scientists measure or calculate the weight of a planet?;Yyaınlanma tarihi: 12 Kasım 2005. Bağlantı: https://www.scientificamerican.com
- Lidbetter, Hugo. (2009). Henry Cavendish and Asperger’s syndrome: A new understanding of the scientist. Personality and Individual Differences. 46. 784-793. 10.1016/j.paid.2009.01.032.
- West JB. Henry Cavendish (1731-1810): hydrogen, carbon dioxide, water, and weighing the world. Am J Physiol Lung Cell Mol Physiol. 2014 Jul 1;307(1):L1-6. doi: 10.1152/ajplung.00067.2014. Epub 2014 May 2. PMID: 24793169.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel