Bilim kurgunun en eğlenceli hikayelerinden biri, Douglas Adams’ın Otostopçunun Galaksi Rehberi’dir. Kitabında bir süper bilgisayara zor bir sorar. Hayata, Evrene ve her şeye dair en büyük sorunun cevabını vermek üzere tasarlandığı bu bilgisayar, cevabın ne olacağını hesaplamak için 7,5 milyon yıl harcar ve sonucunda cevabı bulduğunu söyler. Cevap 42 sayısıdır.

Kitabın yazıldığı zamandan bu güne kadar 42 sayısı ile ilgili birçok teori ortaya atıldı. Birçok tartışmalar yapıldı ve çeşitli filmlerde de bu sayıya referanslar yapıldı. Bu sayede de 42 sayısı modern bir mit haline geldi.
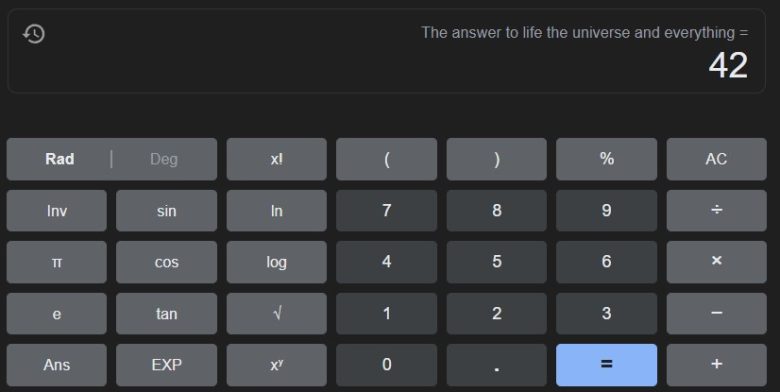
Google arama motoruna hayat, evren ve her şeyin cevabının İngilizce karşılığı olan “answer to life the universe and everything” yazıp aratırsanız karşınızda göreceğiniz 42 sayısı olacaktır. Farklı dillerde de denesiniz, farklı arama motorlarına da sorsanız alacağınız cevap hemen her zaman 42 olacaktır.
Neden 42 Sayısı?
42 sayısı bir dizi ilginç tesadüfte ortaya çıkıyor. Eski Mısır mitolojisinde, ruhların yargılanması sırasında, ölüler 42 yargıç önünde 42 günahtan hiçbirini işlemediklerini beyan etmek zorundaydılar. Antik Tibet’in 42 hükümdarı vardı. Ve MS 836’dan 842’ye kadar (yani, dokuzuncu yüzyılın 42. yılı) hüküm süren Langdarma bunların sonuncusuydu.
Avrupa’da basılan ilk kitap olan Gutenberg İncili, her sütunda 42 satırlık bir metin içerir. Bu nedenle “Kırk İki Satırlı İncil” olarak da adlandırılmaktadır.
Aslında 42 sayısı ile ilgili tesadüfleri anlatan onlarca kitap yazılmıştır. İkili sistemde 42 sayısı 101010 olarak yazılır. Bu da birkaç hayranın 10 Ekim 2010’da (10/10/10) partiler düzenlemesine neden olmuştur. İşin asıl önemli kısmı bu sayının neden seçildiğidir.

Adams’a neden 42 sayısı? diye sorduklarında verdiği cevap, biz insanların belirli gizemleri çözmek konusunda, ne kadar takıntılı olduğumuzun bir kanıtıdır. “Bir sayı olmalıydı, sıradan bir sayı ve ben onu seçtim. Masama oturdum, bahçeye baktım ve 42 olur diye düşündüm. Yazdım. Hikayenin sonu.”
Tüm bunların sonucunda hikayenin sonuna geldiğimizi düşünebilirsiniz. Ancak 42 sayısı hem matematikte hem de fizikte ilginç biçimde karşımıza sık sık çıkar.
42 Sayısı İle İlgili Bazı Özellikler
42 Sayısı Gökkuşaklarında da Karşımıza Çıkar
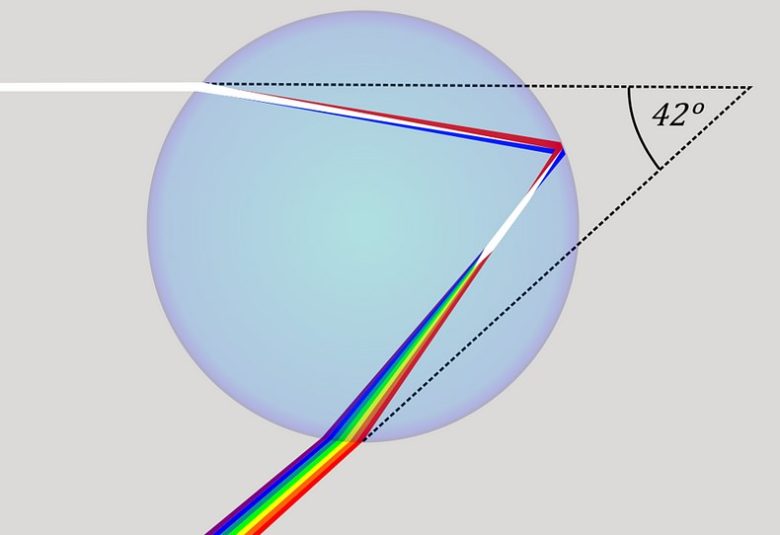
Yağmur damlaları, şelaleler bahçe hortumları ya da benzer bir çok şey bir gökkuşağı yaratmaya yarayacaktır. Ancak hepsinin birkaç ortak noktası var. Hepsi su damlacıklarından yansıyan ışıktan kaynaklanıyor. Hepsi ışık kaynağının yönüne zıt bir yönde ortaya çıkar. Ve hepsi, ışık kaynağı yönünden 42° sapmış yay benzeri bir şekle sahiptir.
Işık havadan suya doğru hareket ettiğinde, farklı dalga boyları farklı açılarda kırılarak renklerin dağılmasına neden olur. Işık, su damlacığının arkasına çarptığında ise geldiği açıyla yansır. Ancak tekrar havaya çıktığında, her dalga boyu orijinalinden belirli bir sapma açısıyla uzaklaşır. Bu sapma açısının ortalaması da 42° olacaktır.
10 sayısını kaç farklı şekilde bölebilirsiniz?
Belirli bir sayıyı oluşturmak için pozitif tam sayıları kaç benzersiz şekilde toplayabilirsiniz? Örneğin 5 sayısı için bunun 7 yolu vardır:
- 1 + 1 + 1 + 1 + 1,
- 1 + 1 + 1 + 2,
- 1 + 1 + 3,
- 1 + 2 + 2,
- 1 + 4,
- 2 + 3,
- 5.
10 sayısı için ise bunu yapmanın 42 benzersiz yolu vardır. Şaşırtıcı bir şekilde, 10 ile 42 arasındaki tek ilişki bu değildir. 10 sayısı 2¹ + 2³, 42 sayısı ise 2¹ + 2³ + 2⁵ olarak yazılabilir. Bu sayıları ikili olarak yazsaydık, “10” sayısı 1010, “42” sayısı ise 101010 olurdu. Bu sayılar ve bu ilişkiler hem matematikte hem de fizikte (özellikle grup teorisi yoluyla) önemli roller oynar
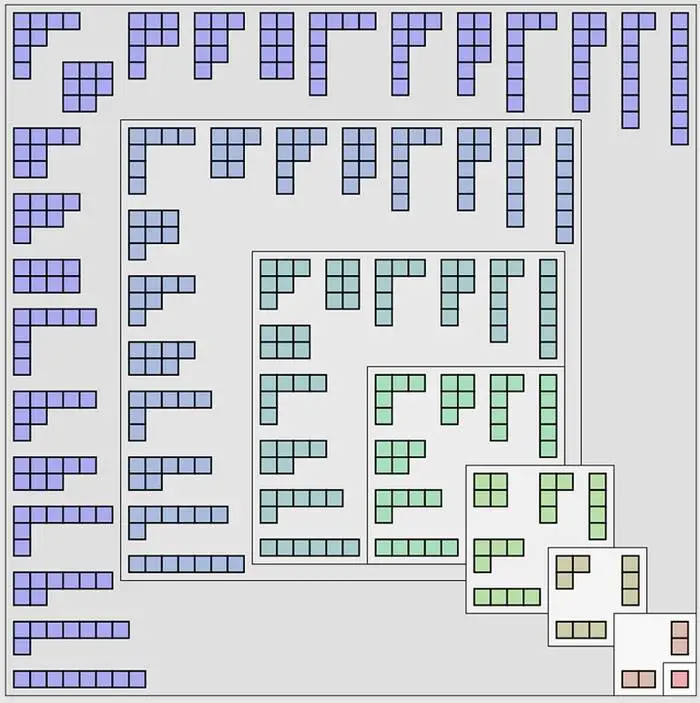
1 sayısının1 yolu vardır (1); 2 için 2 (2, 1+1); 3 için 3 tane var (1+1+1, 1+2, 3), ama 4 için 5 tane var, 5 için 7 var vs. 10 sayısını bölmenin tam olarak 42 benzersiz yolu vardır.
42 Sayısı Pronik Bir Sayıdır
İki ardışık sayının çarpımı olan sayılara pronik sayılar denir. Bu sayılar n.(n+1) biçiminde ifade edilebilir. 42=6×7 olduğu için bu şartı sağlar. İlk bir kaç pronik sayı 0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462… biçimindedir. Ardışık iki pronik sayının aritmetik ortalaması bir kare sayıdır.

42 Sayısı İle Bir İlginç Özellik Daha
İşte size bir matematik bulmacası: (1/ a ) + (1/ b ) + (1/ c ) + (1/ d ) = 1 eşitliğini doğru yapacak a , b , c ve d gibi dört pozitif tamsayı bulabilir misiniz? Örneğin a , b , c ve d’nin tümü 4’e eşitse bu çok basittir. Bu sayılardan ikisinin eşit olmasına izin verirseniz birçok olası çözüm vardır: a =2, b =4 ve c= d =8; a = b =3, c =4, d =12 bunlardan bazılarıdır.
1 = 1/a + 1/b + 1/c + 1/d denkleminin, a, b, c ve d’nin hepsi farklı, pozitif tam sayılar olması durumunda yalnızca birkaç benzersiz çözümü vardır. Bu denklemin çözümü olan en büyük sayı, belki de şaşırtıcı bir şekilde, 42 sayısıdır.
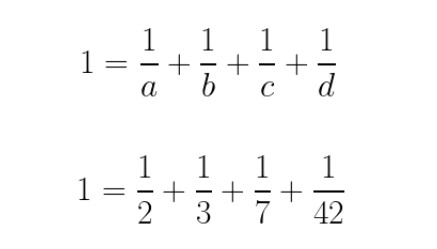
Üç Küp Toplamı Sorusu 42 Severler İçin Sürpriz Oldu
M.S. 3. yüzyılda yaşamış olan İskenderiyeli Diophantine (Diophantus) tarafından ortaya atılan ve günümüzde halen matematikçileri meşgul eden bir problem vardır. Bu problem 1≤k<∞ biçiminde bir k sayısı için k=x3+y3+z3 şeklinde x, y, z gibi herhangi (pozitif veya negatif, istenilen kadar büyük ya da küçük) üç sayının küplerinin toplamı olarak nasıl yazılabileceğini araştırır.
Örneğin 6=23+(-1)3+(-1)3; 20=33+(-2)3+13 ; 51=(-796)3+6593+6023 biçiminde yazılabiliriz. Bu sayılardan bazıları aşağıdadır.
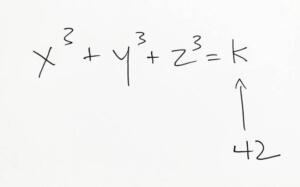
1,2,3,6,7,8,9,10,11,12,15,16,17,18,19,20,21,24,25,26,27,28,29,30,33,34,35,36,37,38,39,42,43,44,45,46,47,48…Dikkat edeceğiniz gibi bazı sayılar eksik. Çünkü 9a+4 ya da 9a+5 (a burada herhangi bir sayı) olarak yazılan sayılar bu kurala uymuyor.
Bu zamana kadar 33, 42, 114, 165, 390, 579, 627, 633 sayıları yazılmayı bekleyen sayılardı. Bunlardan 33 sayısının yazımı 2019 yılında çözülmüştü. Böylece bilmecede sıra 42 sayısına gelmişti. Sonrasında bir ekip, problemin son parçası için de çözüm elde etti. X = -80538738812075974; Y = 80435758145817515; Z = 12602123297335631. Böylece, meşhur Diophantine Denklemi için 1’den 100’e kadar olan tüm k değerleri için hesaplamaları bitirilmiş oldu.
Evren bugün ne kadar hızlı genişliyor?
Belki de 42 sayısı evrenimiz ile ilgili bir gerçeği bize göstermeye çalışıyordur. Bildiğiniz gibi Evren genişliyor ve soğuyor; bu da yoğunluğunun azaldığı anlamına geliyor. Bugün genişleme hızı geçmişte hiç olmadığı kadar yavaştır ve yavaşlamaya da devam etmektedir.
Peki Evren şu anda ne kadar hızlı genişliyor? Her ne kadar bu kozmik bilmeceyi çözmek için daha fazla bilim gerekli olsa da, “42” olası ve hatta muhtemel cevaplar kapsamındadır.

Son olarak 42, Güneş, felaketle sonuçlanan bir kırmızı deve dönüşmeden önce Samanyolu’nun etrafında kaç kez döneceğinin sayısıdır. Bu gerçekten de hayat, Evren ve her şey hakkındaki en önemli sorunun cevabı olabilir.
Kaynaklar ve İleri Okumalar:
- Ian Stewart; Professor Stewart’s Incredible Numbers; Perseus Books ;2015; ISBN: 0465042724
- The Biggest Fundamental Questions That ‘42’ Really Is The Answer To. Yayınlanma tarihi: 1 Ekim 2020. Kaynak site: Big Think. Bağlantı: The Biggest Fundamental Questions That ‘42’ Really Is The Answer To.
- For Math Fans: A Hitchhiker’s Guide to the Number 42. Yayınlanma tarihi: 21 Eylül 2020; Bağlantı: https://www.scientificamerican.com/
Matematiksel