Abraham de Moivre, günümüzde adını verdiği Moivre formülüyle tanınan ünlü bir Fransız matematikçisidir. Kendisi normal dağılım ve olasılık teorisi konusundaki çalışmalarıyla da tanınır. Kendisi ile ilgili ilginç bir anekdot ise, kendi ölüm tarihini hesaplamasıdır.
Moivre’nin ilgi alanlarından biri, ölüm istatistikleri idi. Ölümü sayılarla ilişkilendirmek için önemli miktarda zaman harcadı. Bir kişinin öleceği günü tahmin edebilecek bir teori formüle ettiğine inandı. Bu formül ile yaptığı en isabetli tahmin ise kendi ölüm tarihini hesaplamak oldu. Detayları birazdan aktaracağız. Ancak öncelikle kendisini tanımalısınız.
Abraham de Moivre Kimdir?
1667 yılında Fransa’da doğan de Moivre, matematiğe ve bilimin diğer alanlarına çok sayıda önemli katkılarda bulunduğu uzun ve üretken bir yaşam sürdü. De Moivre’nin erken yaşamı kargaşa ve belirsizlikle şekillendi. Fransa’nın kuzeydoğusundaki küçük bir kasaba olan Vitry-le-François’de Protestan bir ailenin çocuğu olarak dünyaya gelmişti. O dönemde Fransa bir dizi dini çatışmanın ortasındaydı ve Protestanlar ciddi zulüm ve ayrımcılığa maruz kalıyordu. Bu nedenle, De Moivre henüz 11 yaşındayken ailesi İngiltere’ye kaçtı.
Hayatının ilk yıllarında karşılaştığı zorluklara rağmen de Moivre yetenekli bir matematikçi olduğunu kanıtladı. Tanınmış matematikçi James Hodgson’un vesayeti altında matematik çalışmaya başladı ve kısa sürede konuya büyük bir ilgi duydu. De Moivre’nin yetenekleri bu alandaki diğer kişiler tarafından fark edildi ve 1697’de Kraliyet Cemiyeti’ne atandı.
Büyük bir matematikçi olarak tanınmasına karşı, özel matematik dersleri, sigorta ve kumar konularında danışmanlık yaparak geçimini zorlukla sağladı. Yaşamı yoksulluk ve açlık içinde geçirdi. Bu yüzden de hiç evlenmedi. Arka arkaya yaptığı bir çok değerli çalışmaya rağmen üniversiteler ve bilim çevreleri onu koruyamadı. Bu değerli matematikçi 27 Kasım 1754 yılında da aramızdan ayrıldı.
Bilimsel Çalışmaları
Olasılık kuramının kurucularından biri olarak kabul edilen De Moivre analitik geometrinin de gelişimini sağlayan çalışmalar yaptı. 1711 yılında en ünlü eseri olan “Şans Doktrini – ”The Doctrin of the Changes” adlı çalışmasını kaleme aldı.
Olasılık teorisi üzerine ikinci önemli çalışması 1730 yılında yayınladığı “Miscellanea Analytica” adlı eseridir. James Stirling’e atfedilen Stirling formülünü ilk kullanan De Moivre’dir. De Moivre “Herhangi bir meblağı kaybetme riski, beklentinin tersidir. Bu riskin gerçek ölçümü, tehlikeye atılan meblağın, kaybetme olasılığı ile çarpımına eşittir.” diyerek iktisattaki “beklenen kayıp değerin” formülünü de verir. Ayrıca standart sapma kavramını kullanmasıyla risk ölçümünde çağdaş tekniklerin temelini meydana getirir.
De Moivre’nin istatistiğe dolayısıyla bilime en büyük katkısı 1730 yılında sunduğu ve “merkezi limit teoremi” olarak bilinen “büyük sayılar kanununun” öncüsü olmasıdır. Büyük sayılar kanunu ilk kez Jakob Bernoulli tarafından yayınlanmıştır. Bu kanuna göre aynı deney, birbirinden bağımsız rasgele çok sayıda yapıldığında, ortalamalar beklenen değere (beklenen ortalamaya) yakınsayacaktır. Yani uzun vadede gözlem sayısı arttıkça deneylerin ortalaması istikrarlı olacak ve belli bir merkezde dengelenecektir.
De Moivre formülü
De Moivre’nin bu çalışması, normal dağılımın yapısını ortaya koyması ve standart sapmanın ilk kez sunulması bakımından oldukça önemlidir. Meşhur çan eğrisini öğrenciler, istatistikçiler ya da yolu istatistikten geçenler iyi bilirler. Bu eğri özellikle öğrencilerin sınav puanlamalarında deyim yerindeyse hayat kurtarıcı olmaktadır. “Çan eğrisini“ Gauss’dan önce ilk kullanan kişidir.
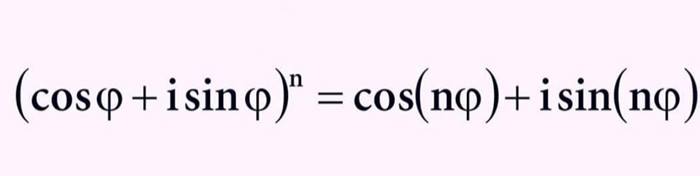
Matematiğe en büyük katkılarından biri kendi adıyla anılan 1722 yılında tanımladığı De Moivre formülüdür. Bu formülün önemi karmaşık sayılar ile trigonometri arasındaki bağlantıyı açıklamasındadır.
Matematik dışında astronomiye yönelik çalışmaları da vardır. Matematik bilimine yaptığı önemli katkılar dolayısıyla 1735’te Berlin Prusya Bilim Akademisi ve 1754’te Paris Fransız Bilimler Akademisi üyeliklerine kabul edilmesi ile şereflendirilmiştir.
De Moivre Ölüm Tarihini Nasıl Hesapladı?
De Moivre, matematik alanındaki çalışmalarının yanı sıra astronomi ve fizik gibi bilimin diğer alanlarıyla da ilgileniyordu. Özellikle yakın ilişki içinde olduğu Isaac Newton da dahil olmak üzere, zamanının önde gelen bilim adamlarının çoğuyla yazıştı.
Şimdi işin ilginç kısmına gelelim? Kendisi gerçekten ölüm tarihini hesaplamış olabilir mi? Sık tekrarlanan hikaye şu biçimdedir.
Hayatının son yıllarında de Moivre giderek daha uzun saatler uyumaya başladığını fark eder. Uyku alışkanlıklarını not ettiğinde her gece fazladan 15 dakika uyuduğunu görür. De Moivre, ölümünün kesin tarihini hesaplamak için bu bilgiyi kullanabileceğine ikna olur. Matematikçi, bu fazladan 15 dakikanın 24 saate ulaştığı gün öleceğini hesap eder. Sonucunda hesaplarına göre ölüm tarihi 27 Kasım 1754 olacaktır. Nitekim haklı çıkarak hesaplamış olduğu günde de vefat eder.
De Moivre’nin ölüm tahmininin hikayesi sıklıkla karşımıza çıksa da, bunun doğru olup olmadığı tam olarak belli değil. Bazı tarihçiler, hikayenin de Moivre’nin ölümünden sonra uydurulduğunu düşünüyor. Hikaye karşımıza, Helen M. Walker tarafından kaleme alınan, 1934 tarihli De Moivre biyografisinde karşımıza çıkıyor. O da bunu başka kaynaklardan aldığını ifade ediyor. Ancak ilk kaynak belirsiz.
Sonuç olarak, De Moivre’nin hayatının sonuna doğru giderek zayıflayan bir durumda olduğu doğrudur. Günde 20 saatten fazla uykuya ihtiyacı vardı ve bu durumu daha da kötüleşti. Resmi ölüm nedeni somnolans yani uzun süren patolojik bir uyku durumuydu. Ancak onun ölümü hakkında kesi bildiklerimiz bu kadardı.
Sonucunda bazı gizemler de kişiler gibi tarihe gömülür. Aynı şey De Moivre’nin sonu için de geçerli. Her ne kadar kendi ölümüyle ilgili tahmini onunla ilişkilendirilen en ünlü hikaye olsa da, onu bilim tarihinde benzersiz ve önemli bir figür olarak gerçekten farklı kılan şey onun sayısız başarısı ve matematik dünyasına yaptığı katkılardır.
Kaynaklar ve İleri Okumalar:
- Schneider, I. Der Mathematiker Abraham de Moivre (1667–1754). Arch. Hist. Exact Sci. 5, 177–317 (1968). https://doi.org/10.1007/BF00411630
- Moivre, Abraham De; https://www.encyclopedia.com/
- Abraham de Moivre; https://mathshistory
Matematiksel
Elinize sağlık , güzel bir çalışma olmuş 👏
özellikle Matematik derslerinde bu alana katkı sağlayan kişilere ait bilgiler verilmesi derslere olan ilgiyi artıracağını düşünüyorum
Teşekkür ederiz emekleriniz için