1904’te Fransız matematikçi Henri Poincare üç boyutlu uzaylar (manifoldlar) hakkında önemli bir soru sormuştu. Rus matematikçi Grigori Perelman’da, Clay Matematik Enstitüsü tarafından 2000 yılında ortaya konan yedi Milenyum probleminden biri olan bu soruyu yani Poincare varsayımını çözerek adını bir ilke yazdıracaktı.

Poincare Varsayımı şimdiye dek çözülen tek Milenyum problemidir. Ancak bu problemi muhtemel esas unutulmaz kılan Grigori Perelman’ın 1.000.000 dolarlık Milenyum Ödülü’nü geri çevirmesidir. ( Neden geri çevirdiğine dair detaylar burada: Grigori Perelman Kendisine Verilen Ödülleri Neden Kabul Etmemişti?)
Kısaca Henri Poincare Kimdir?
19. yüzyılın sonlarında Paris dünya matematiğinin merkezi konumundaydı ve Henri Poincare de onun öncü ışığıydı. Bertrand Russel’a “Fransa’nın yetiştirdiği en büyük adamı kimdir?” diye sorulduğunda cevabı tereddütsüz bir şekilde Henri Poincare olmuştu. Poincare matematiğin tüm dallarında genel bir fikir sahibi olan evrensel matematikçilerin son örneklerinden biriydi.

Jules-Henri Poincare, 29 Nisan 1854’te dünyaya geldi. İleri derece miyop ve fiziksel olarak zayıf bir çocuktu. Buna rağmen entelektüel yetenekleri ile bu eksiklikleri kısa sürede telafi etti. Okuma belli başlı eğlencesiydi. Üstün bir bellek ve hatırlama yeteneğine sahipti.
15 yaşında doğru matematiğe ilgisi artmaya başladı. Tüm matematik işlemlerini kafasında yapıyor, sonuca ulaştıktan sonra kağıda döküyordu. Etrafındaki gürültü ya da konuşmalar onu rahatsız etmiyordu. Bilimsel çalışmalarının çoğunu da aynı biçimde gerçekleştirdi. 1873’te Ecole Polytechnique’e girdi ve iki yıl sonra mezun oldu.
Bu okulu bitirdikten sonra mühendis olmak için, Yüksek Maden Okulu’na girdi. Kısa süre maden mühendisi olarak çalıştıktan sonra kendini matematiğe adamaya karar verdi. Bu nedenle, 1879’da Caen’da analiz profesörü olarak işe başladı. 27 yaşında Paris Üniversitesi’ne geçti. Sorbonne’da mekanik ve deneysel fizik dersleri verdi. Hayatının geri kalan kısmını Paris’te, Fransız matematiğinin itiraz kabul edilmez üstadı olarak geçirdi.
Henri Poincare’nin Matematiğe Katkıları Nelerdir?

Henri Poincare’nin yaratma devresi, 1878 yılında doktora tezi ile başlamıştır ve ancak ölümüyle bitmiştir. Bu süreçte, beş yüz kadar çalışma gerçekleştirmiştir. 1880 yılında eliptik fonksiyonlar üzerindeki en parlak keşfini 26 yaşında yapmıştır. Möbius dönüşümlerinin bir grup oluşturduğunu göstermiştir. Bu yaptıklarını, Möbius grupları ismi altında incelemiştir.
Otomorfik fonksiyonlar ve otomorfik gruplar onun çalışmalarıdır. Poincaré gök mekaniği ile de ilgilendi. Üç cisim problemi üzerine yaptığı araştırmada, modern kaos teorisinin temellerini atan bir kaotik determinist sistemi keşfeden ilk kişi oldu.
Cebirsel topoloji, 19. yüzyılın sonlarında Henri Poincaré’nin çalışmasıyla başladı. Geometri ve topolojideki zor problemleri cebire dönüştürerek, karmaşık matematiksel nesneleri anlamanın bir yolunu sağladı. Poincaré’nin zamanından bu yana, cebirsel topoloji kendi başına önemli bir matematik alanı haline geldi.
Poincaré, yaşamı boyunca çok sayıda ödülle onurlandırıldı. 1887’de Bilimler Akademisi’ne seçildi ve 1906’da başkanı oldu. Henri Poincare geçirdiği ameliyat sonrası 17 Temmuz 1912’de elli sekiz yaşında beklenmedik bir biçimde yaşamını yitirdi.
Poincare varsayımı nedir?

Poincaré, topolojinin temelini atarken, aynı zamanda topolojinin en basit üç boyutlu nesnesinin, dört boyutlu bir yüzeyi belirlemek için yeterli araçlara sahip olup olmadığını düşünüyordu. Bu düşünce onu, tüm zamanların en meşhur sorularından birine yönlendirdi. Hiçbir belirleyici niteliği ( delik, kulp, büküm vs) olmayan bir üç-boyutlu uzay, mutlaka üç-boyutlu bir küre mi olmak zorundadır? İşte bu soru Poincare varsayımının temeliydi.
Poincare Varsayımı üzerine pek çok girişim oldu. Bill Thurston, 1970’lerin sonlarında üç boyutlu uzayları anlama konusunda muazzam ilerlemeler kaydetti. Özellikle Poincaré’den bu yana yapılan tüm çalışmaların esasen tek bir temaya uyduğunu fark etti. Bilinen üç boyutlu uzayların doğal bir şekilde parçalara bölünebileceğini, böylece her parçanın düzleme ve yuvarlak küreye benzer şekilde tekdüze bir geometriye sahip olabileceğini gözlemledi.

Onun fikirleri oldukça önemliydi. Sonucunda bu varsayımlar ile matematikçilere üç-boyutlu uzayları sınıflandırma şansı doğmuş olacaktı. Teorilerini daha da geliştiren, özellikle de herhangi bir uzayın geometrik yapısını bulmaya çalışan güçlü bilgisayar programları üreten birçok parlak öğrencisi vardı.
1982’de Richard Hamilton, geometrik analizde Ricci akışı adını verdiği yeni bir tekniği tanıtan güzel bir makale yayınladı. Kendisi aslında ısı akışı ile ilgileniyordu. Ancak uzayın geometrik şekli için de benzer bir akışın olması gerektiğini düşündü. Ricci akışı ve diğer benzer akışlar, hareketli ara yüzler, akışkanlar mekaniği ve bilgisayar grafikleri gibi alanlardaki uygulamalarla büyük bir araştırma alanı haline geldi.
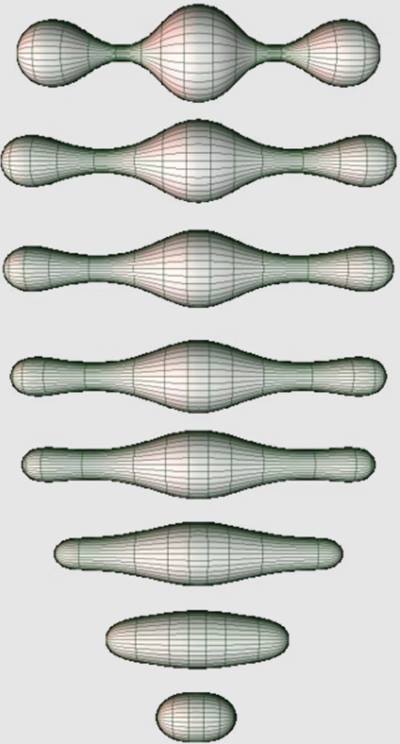
Hamilton, bu olguyu tam olarak anlamak ve Thurston’un öngördüğü geometrik yapı bulunana kadar parçaların Ricci akışı altında gelişmeye devam etmesine izin vermek için çok çalıştı. İşte tam bu sırada Perelman işin içine dahil olacaktı. Bu da varsayımın çözülmesini sağlayacaktı ( Çözüm detayları bu yazının kapsamının dışındır.) Poincare’nin fikir ve yöntemleri günümüzde, özellikle cebirsel topoloji, karmaşık analiz ve farklı geometrilerde yapılan modern araştırmalar üzerinde etkisini sürdürmeye devam ediyor.
Yazının devamında göz atmanızı öneririz: Henri Poincaré Matematik Sayesinde Adaleti Nasıl Sağladı?
Kaynaklar ve ileri okumalar:
- Henri Poincare And The Chaos Theory; https://www.storyofmathematics.com/
- Ioan James; Büyük Matematikçiler; TÜRKİYE İŞ BANKASI KÜLTÜR YAYINLARI, 2009; ISBN 978-605-360-760-1
- Ali Dönmez, Dünya Matematik Tarihi; Matematiğin Öyküsü ve Serüveni; Fransız Matematikçiler
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel



