Alışverişe çıkmak başta heyecan verse de para ödemek için kasaya ilerlediğinizde süreç genelde bir kabusa dönüşür. Kendinize göre en kısa kuyruğu seçip beklemeye başladığınızda, az evvel hızla ilerleyen kuyruk sanki yavaşlamış gibidir. Bu sırada da yan taraftaki kuyruk daha hızlı ilerlemeye başlar. Peki, zamandan tasarruf etmek adına doğru kuyruğu nasıl seçeceğiz?

Aslında matematikçiler buna bir çözüm üretmek için yıllardır çalışıyor. Sadece bu konuyla ilgilenen bir matematik dalı bile var. Buna kuyruk teorisi denir.
Kuyruk Teorisi Nedir?
Kuyruk teorisi, kuyruğa girmenin veya sıra beklemenin matematiksel çalışmasıdır. Bir kuyruk sistemi, bir varış sürecinden (müşterilerin kuyruğa nasıl geldiği, toplamda kaç müşterinin bulunduğu), kuyruğun kendisinden, bu müşterilere katılmak için hizmet sürecinden ve sistemden ayrılmalardan oluşur.
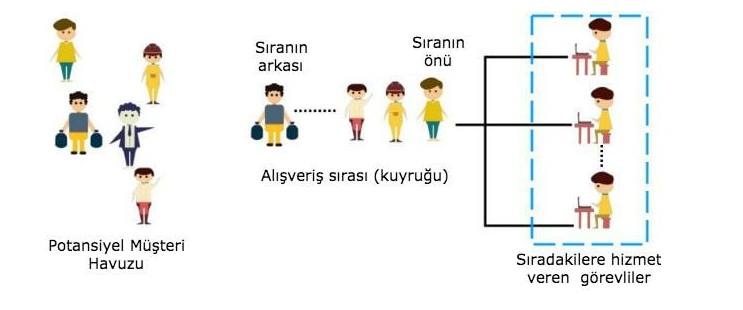
Davranışsal ekonominin önemli teorilerinden biri olan Kuyruk Teorisi, ortalama bekleme süresi ve kuyruk uzunluğu gibi kritik faktörleri hesaplamamızı sağlar. Hesaplamalar sonucunda “bir müşterinin sırada 10 dakika bekleme olasılığı nedir? Müşteri başına ortalama bekleme süresi nedir?” gibi sorulara cevap bulunmaya çalışılır.
Bir bankada veya bir mağazada sıra beklemek, arama beklemeye alındıktan sonra bir müşteri hizmetleri temsilcisinin aramayı yanıtlamasını beklemek, bir trenin gelmesini beklemek, bir bilgisayarın bir görevi gerçekleştirmesini veya yanıt vermesini beklemek kısacası beklemek ile ilgili her şeyde kuyruk teorisi arka planda bir yerlerde kendine bir yer bulacaktır.
Kuyruk Teorisinin Arka Planındaki Matematik
Kuyrukların ilk matematiksel çalışması 1909’da Kopenhag Telefon Şirketi’nden Agnar Krarup Erlang tarafından yapıldı. Amaç, uygun hizmet sunmak için, kaç telefon hattına ve kaç operatöre ihtiyaç olduğunu bulmaktı. Bunun sonucunda, ortalama bekleme süresini hesaplamak için bugün hala kullanılan bir denklem türetti.
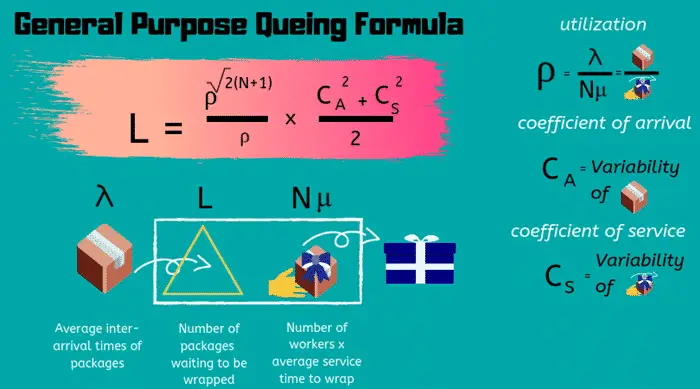
Kuyruk teorisinin arka planındaki matematik zordur. Bu nedenle bu yazıda matematiksel hesaplamalar girmemiz olası değildir. Matematiğin zorluğu temelinde kuyrukların belirsizliklerinden gelir. Sonucunda müşteriler genellikle düzenli aralıklarla gelmezler.
Bu nedenle varış zamanları stokastik süreç olarak adlandırılmaktadır. ( Zaman içerisinde önceden kestirilemeyecek şekilde gelişen süreçlere Stokastik yani Rastgele süreçler denir. Bu tür stokastik problemler için de çözüm sağlayan genel bir formül bulmak genellikle zordur. Bilgi için bu yazımıza göz atabilirsiniz: Stokastik Süreçler ve Markov Zincirleri Nedir?)
Kuyruk yasası hesaplamaları ile ilgili hesaplamalar Little Yasası adı verilen bir matematiksel teoreme dayanır. Adını da operasyon araştırmaları konusunda uzmanlaşmış bir MIT profesörü olan yaratıcısı John Dutton Conant Little’dan alır. Little yasası, bir kuyruktaki ortalama öğe sayısının, öğelerin sisteme ulaşma ortalama hızının sistemde geçirdikleri ortalama süre ile çarpılmasıyla hesaplanabileceğini belirtir.
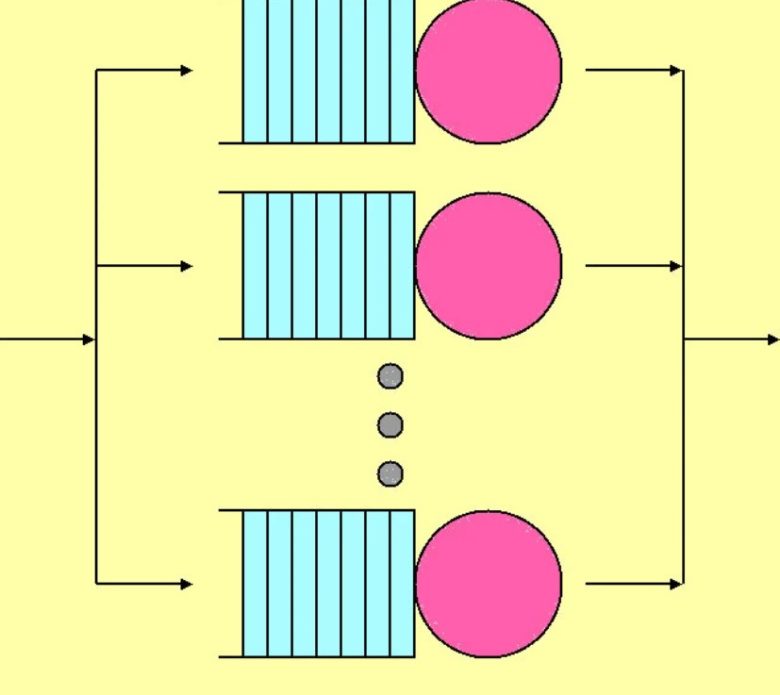
Matematiksel gösterimde Little yasası şöyledir: L = λW. Burada L, ortalama öğe sayısı; λ, kuyruk sistemindeki öğelerin ortalama varış zamanı ve W, öğelerin kuyruk sisteminde geçirdiği ortalama süredir. Little yasası bütün kuyruklar için geçerli değildir. Sistemin “kararlı bir durumda” olduğunu varsayar. Yani sistemi karakterize eden matematiksel değişkenler zamanla değişmez.
Little yasası yalnızca üç girdiye ihtiyaç duysa da, birçok kuyruk sistemine uygulanır. Bir kuyruğun belirli bir süre içinde nasıl performans gösterdiğini analiz etmede veya bir kuyruğun şu anda nasıl performans gösterdiğini hızlı bir şekilde ölçmede yararlı bir araçtır.
Örneğin: bir ayakkabı kutusu şirketi, bir depoda saklanan ortalama ayakkabı kutusu sayısını bulmak istesin. Şirket, yılda 1.000 ayakkabı kutusu geldiğini biliyor. Bu kutular depoda yaklaşık 3 ay (1/4 yıl) kalıyorsa, sayım yapmadan depodaki ortalama ayakkabı kutusu sayısı 250 olarak bulunacaktır.
Feller Paradoksu Nasıl Çalışır?
Ne yazık ki, bir mağazaya girdiğinizde ilgili değişkenlerin tam olarak ne olduğunu bilmeniz mümkün olmaz. Bu nedenle yukarıda sizlere aktardığımız matematik fazla da işe yaramaz. Bu noktada da işin içine psikolojik faktörler karışır.

Bir kuyruğa girdiğinizde doğru seçimi yapıp yapmadığınızı bilmek isteyeceksiniz. Mesela sizin kasanızdaki kasiyer en hızlısı mı? Sıradaki ilk kişinin hizmet alması için gereken süreyi ölçmeye çalışırsanız, muhtemelen yanlış sırayı seçtiğiniz duygusuna kapılırsınız. Buna, Feller paradoksu denir. Teknik olarak, bu gerçek bir mantıksal paradoks olmasa da sonuç sezgilerimize aykırıdır.
Feller paradoksu şöyle işliyor. Bir bankanın iki hizmet sunduğunu varsayalım. Birinci hizmet eşit olasılıkla 0 ya da 5 dakika sürsün. Diğer hizmet ise yine eşit olasılıkla, 10 ya da 20 dakika sürsün. Bir müşterinin her iki hizmeti seçmesi eşit derecede olasıdır.
Bu nedenle bankanın ortalama hizmet süresi 8.75 dakikadır. Bir işlem sırasında siz de sıraya girerseniz 0 dakika ihtimali geçerli olamayacağına göre sizden önceki müşteri 5, 10 ya da 20 dakikalık servisi kullanıyor olmalıdır.
Bu da ilk ortalama olan 8.75 dakikadan daha fazla bekleme süresi demektir. Aslında, aynı durumla karşılaştığınız üç seferden ikisinde, önünüzdeki müşteri 10 ya da 20 dakika hizmet almaktadır. İşte bu nedenle girdiğiniz sıra hiç bitmeyecek gibi gözükmektedir. Kısacası hissettiğiniz duygu tamamen psikolojik değildir.
En Hızlı Kuyruğu Seçmek İçin Bazı Öneriler

Araştırmalar, insanların çoğunun (sağ ellerini kullanmaları nedeniyle) sağdaki kuyruğu seçme eğilimi gösterdiklerini ortaya koymuştur. Yani çok sayıda paralel kuyruk varsa soldaki kuyruğu seçmek aynı zamanda en kısa kuyruğu seçmek anlamına gelir.
Kulağa saçma gelse de uzmanlar çok fazla sayıda ürün almış müşterilerin işlemlerini yapmanın kasiyerlerin daha hünerli ve hızlı olmasını sağladığını düşünmektedir. Sonucunda kasiyer bir an önce önündeki yığını eritmek için maksimum verimle çalışmak isteyecektir.
Ayrıca bir kuyruğun hızı sadece önünüzdeki insan sayısına da bağlı değildir. Müşterilerin yaşları ve ne aldıkları da önemlidir. Örneğin yaşlı insanlar daha yavaş hareket ederek kuyruğun yavaşlamasına neden olurlar. Ayrıca satın alınan ürünler de önemlidir. Aynı üründen çok sayıda alınmışsa işlem daha kısa sürer. Ancak sebze meyve gibi tartılarak fiyatı belirlenmesi gereken ürünler aldıysa işlem daha uzun sürecektir.
Ayrıca kuyrukta beklerken kasiyeri göremiyorsak (kasiyeri görmemizi engelleyen bir kolon, raf vb. varsa) bekleme süresini olduğundan daha uzun olarak algılıyoruz. Kasiyerin işini yaptığına tanık olmak bize kuyruk daha hızlı ilerliyor gibi hissettirecektir.
Sonuç olarak;
Bir işletmenin karlılığı açısından kuyruklar son derece önemlidir. Ancak uzun kuyruklar insanları alışveriş yapmaktan da vazgeçirebilir. Günün sonunda kuyruk teorisi hem işyerleri hem de bizler için en verimli süreci belirlemeye çalışacaktır.
Kaynaklar ve ileri okumalar:
- There’s a mathematical formula for choosing the fastest queue. Yayınlanma tarihi: 7 Mayıs 2017; Kaynak site: Conversation. Bağlantı: There’s a mathematical formula for choosing the fastest queue/
- Shunko, Masha & Niederhoff, Julie & Rosokha, Yaroslav. (2016). Humans Are Not Machines: The Behavioral Impact of Queueing Design on Service Time. SSRN Electronic Journal. 10.2139/ssrn.2479342.
- An Introduction to Queuing Theory. Bağlantı: https://www.thoughtco.com/queuing-theory-4171870
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel