
Diyelim ki okula ya da işe gidiyorsunuz ve bunun için otobüs kullanmayı tercih ediyorsunuz. Durağa vardınız. Ancak geç kalmamanız da gerekiyor. Acaba otobüs gelmeden önce ne kadar beklemeniz gerekiyor?
Şaşırtıcı bir şekilde, cevap bir otobüs tarifesine bakarak tahmin edebileceğinizden çok daha uzun. Bu yazıda gelin bunun cevabını, bekleme süresi paradoksu olarak adlandırılan bir fenomeni birlikte keşfedelim.
Bir otobüs durağına vardığınıza zaman, aşağıda görmüş olduğunuz otobüs bekleme çizelgesine bakarak, beklemeniz gereken zamanın ortalama 6 dakika olması gerektiğini tahmin edebilirsiniz. Otobüs durağına geldiğiniz zaman çizelgede bir saat içinde 10 otobüs olduğu yazdığını kabul edelim.
Bu, ortalama her 6 dakikada bir otobüs anlamına gelir. 9:00’dan sonraki ilk üç otobüsün 9:01, 9:06 ve 9:09’da varması planlanıyor. Ancak bu zaman elbette sizin durağa varışınıza göre değişecektir. Bu nedenle aslında 1 dakika da bekleyebilirsiniz, 5 dakika da.
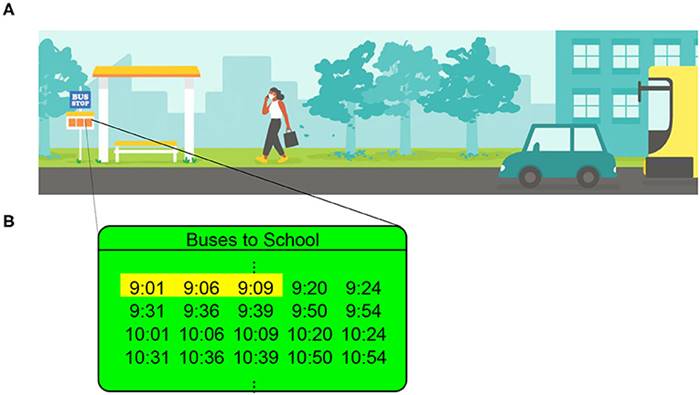
Aslında, bekleme süreniz için akıllıca bir tahmin 3 dakikadır. Bu da otobüsler arasındaki ortalama sürenin yarısıdır. Ancak ne yazık ki, muhtemelen 3 dakikadan daha fazla beklemek zorunda kalacaksınız. Hatta 6 dakikadan bile fazla beklemeniz gerekebilir.
İşte bu duruma bekleme zamanı paradoksu denir. ( Waiting time paradox – bus paradox). Aslında bu paradoks matematiksel bir olgudur ve temelinde otobüsler ile bir ilgisi yoktur.
Bu paradoksun neden oluştuğunu anlamak için aşağıdaki çizelgeye göz atalım. Gördüğünüz gibi otobüsler, 4 dakikalık veya 12 dakikalık aralıklarla geliyor. Bu durumda 1 saat içinde 6 tane otobüsün 4 dakikada 1 ve 3 tane otobüsün 12 dakikada bir geldiğini çizelgeden görebilirsiniz. ( A – Kırmızı ve mavi)
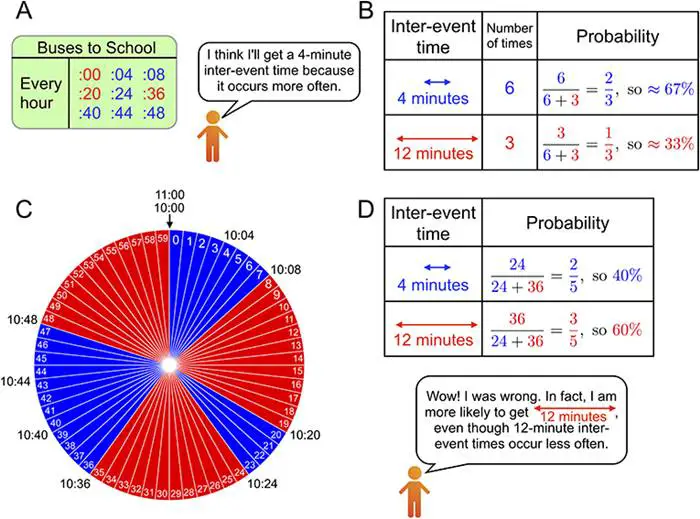
Bekleme Süresi Paradoksu Neden Gerçekleşir?
Şimdi işin içine olasılık hesaplarını ekleyelim. Rastgele bir zamanda otobüs durağına vardınız. Eğer 4 dakika aralıklı otobüs çizelgesine denk geldiyseniz fazla beklemeniz gerekmeyecektir. Yukarıda gördüğünüz gibi aslında 4 dakikalık bir aralığa denk gelmeniz ( yaklaşık yüzde 67), 12 dakikalık bir aralığa denk gelmenizden ( yaklaşık yüzde 33) daha fazla ihtimale sahiptir. ( Hesaplamalar için B kısmına göz atınız.)
Ancak ne yazık ki, bu bir temennidir. Bizim senaryomuzda bir sonraki otobüsün ne zaman geleceğini bilmeden otobüs durağına geldiğinizi hatırlayın. 4 dakikalık zaman dilimine denk geldiyseniz bir sonraki otobüsü çok uzun süre beklemezsiniz. Ancak 12 dakikalık dilimdeyseniz, uzun süre beklemeniz gerekebilir.
Bir otobüse binmek için beklememiz gereken sürenin tahmini çarkın her bir 0’dan 59’a kadar sayılar olan bir çarkı döndürmeye ve rastgele bir noktada durdurup gelen sayıyı söylemeye benzer. ( Yukarıda C bölümüne bakınız). Parmağınız 33’ü gösteriyorsa otobüs durağına 10:33’te varıyorsunuz demek olsun. Bu durumda 10:36’da gelen bir sonraki otobüs için 3 dakika beklemeniz gerekiyor.
Çarkta 24 mavi dakika ve 36 kırmızı dakika olduğunu görüyoruz. Bu durumda 12 dakikalık bekleme süresine denk gelme ihtimalimiz ( yüzde 60) daha yüksektir. Bu cevap sizi şaşırtabilir. Ancak çarkımızdaki dilim sayısına baktığımız zaman kırmızı dilimlerin, mavi dilimlerden daha fazla olması yüzünden kımızı seçme ihtimalimiz daha fazladır.
Tüm olaylar arası sürelerin 6 dakika uzunluğunda olduğunu, yani otobüslerin tam olarak her 6 dakikada bir geldiğini varsayalım. Bu durumda, artık bir bekleme süresi paradoksu yoktur. Bekleme süresi paradoksunun gerçekleşmesi için, 4 dakika ve 12 dakika gibi en az iki olay arası sürenin bir karışımına ihtiyacımız var.
Bekleme Süresi Paradoksu Başka Nerede Karşımıza Çıkar?
Aslında size yazının başında konunun otobüsler ile ilgisi olmadığını söylemiştik. Olaylar arası zamanlar yani olayların hangi sıklıkla gerçekleştiği birçok durumda önemlidir. Bu konu ile ilgili bir başka ünlü örnek ise arkadaşlık paradoksudur. Arkadaşlık paradoksuna göre, arkadaşlarınız sizden daha fazla arkadaşa sahip olma eğilimindedir.
Örneğin bir sınıftaki öğrencilerden biri olduğunuzu ele alalım. Örneğin sınıfınızda, Ayşe’nin sadece bir arkadaşı varsa, sizin o kişi olma olmanız pek olası değildir; başka biri olma olasılığı daha yüksektir. Buna karşılık, Banu sınıftaki öğrencilerin yarısı ile arkadaşsa, o zaman Banu’nun arkadaşlarından biri olma ihtimaliniz daha fazladır.

Her birinin dört arkadaşı olan altı öğrenci ve her birinin 12 arkadaşı olan üç öğrenci olduğunu varsayalım. Bu 9 öğrenciden sadece biriyle arkadaşsanız, arkadaşınızın 12 arkadaşı olan bir kişi olması muhtemeldir. Aslında bu rakamlar yukarıdaki otobüs örneğimiz ile gösterdiğimiz ile aynı sayılar.
Paradoksun nedeni, arkadaş ağlarının yapısı ile ilgilidir. Herhangi bir ağda, birkaç kişi diğerlerinden daha popülerdir; ortalama olarak, ağlarındaki diğer insanlardan daha fazla sayıda arkadaşları vardır.
Bu nedenle, Twitter’da takip ettiğiniz kişilerin sizden daha fazla takipçisi olması ve Facebook’taki arkadaşlarınızın çoğunun sizden daha fazla arkadaşı olması ihtimali yüksektir. Daha fazlası için: Arkadaşlık Paradoksu: Herkesin Sizden Çok Arkadaşı Olmasının Cevabı
Görmüş olduğunuz gibi bekleme süresi paradoksu ile arkadaşlık paradoksu aslında aynı matematiksel altyapıya sahiptir. Matematik görünüşte farklı fikirleri birleştirmenin ve yakından ilişkili olduklarını görmenin bir yolunu sağlar. Bu da güzel bir örnektir. Hazır konu otobüslerden açılmışken bu paradoks ile ilgisi olmasa da ilginizi çekecek küçük bir araştırmadan bahsedelim.
Otobüs Durağında Bekleme Formülü

Durağa vardınız, ama az evvelki süreçte aktardığımız gibi şansınız yaver gitmedi ve otobüs gelmiyor. Gideceğimiz yol da çok uzak değil. Bu durumda acaba otobüsü beklemeye devam mı etmeliyiz, yoksa yürümeye mi başlamalıyız?
İyisi mi siz siz olun gelecek sefer otobüsünüzü bekleyin. Matematikçilere göre hemen her zaman en iyi strateji bu! Harvard Üniversitesi’nde matematik, ekonomi ve etnometikoloji üzerine çalışan Scott Kominers, durakta beklemekte sıkılan ve bu konuya kafa yormaya başlayan matematikçilerden.
Kendisi ve arkadaşları sonunda işin içine oyun teorisini sokarak bir otobüsü ne kadar beklemeniz gerektiğini gösteren bir formül bulmuş. Çalışmayı incelemek isterseniz: https://arxiv.org/abs/0801.0297. Ancak otobüs seferleri arasındaki sürenin bir saati aşması ve gideceğiniz yerin 1 kilometreden kısa olması gibi durumlarda bu teori işe yaramıyor.
Bu arada eğer tercihiniz yürümek ise bunu durakta beklemeye başlamadan vermeniz de size zaman kazandırıyor. Matematiğin hiç tahmin etmediğiniz sorulara cevaplar verebilmesi gerçekten bizce etkileyici…
Kaynaklar ve İleri Okumalar:
- Masuda N and Porter M (2021) The Waiting-Time Paradox. Front. Young Minds. 9:582433. doi: 10.3389/frym.2020.582433; yayınlanma tarihi: 26 Şubat 2021; Bağlantı: https://kids.frontiersin.org/
- Math explains why your bus route seems so unreliable; yayınlanma tarihi: 29 Temmuz 2018; Bağlantı: https://theconversation.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










