Din ve matematik birbiri ile ilgisiz iki konu gibi gelecektir. Ancak tarih boyunca bir çok matematikçi bu ikisini birleştirmeyi, Tanrı’nın varlığını matematik yardımı ile kanıtlamayı denemiştir.

Yüzyıllar boyunca bazı matematikçiler Tanrı’nın varlığını ispatlamaya çalıştı. Bu isimler arasında 17. yüzyılda Blaise Pascal ve René Descartes, 18. yüzyılda Gottfried Wilhelm Leibniz ve 20. yüzyılda Kurt Gödel yer alıyor. Gödel’in bu konuda yazdığı metinler 1987 yılında yayımlandı.
Dahası, 2013’te yayımlanan bir ön çalışmada, bir algoritmik ispat sistemi Gödel’in mantık zincirini inceledi ve doğru olduğunu doğruladı. Peki, matematik sonunda ateistlerin tüm iddialarını çürütmüş mü oldu? Muhtemelen tahmin edebileceğiniz gibi, böyle bir şey olmadı. Gödel, kendisinin “ilahi” olarak tanımladığı bir varlığın belirli varsayımlardan mantıksal olarak çıkarılabileceğini gösterdi..

Pascal’ın Tanrı’nın Varlığına Dair İspatı
Leibniz, Descartes ve Gödel, Tanrı’nın varlığını sadece olasılığından hareketle mantıksal çıkarımla kanıtlamaya çalışan ontolojik bir yaklaşım benimsedi. Pascal ise farklı bir yol izledi. Günümüzde oyun teorisine benzeyen bir yöntemle konuyu değerlendirdi ve ünlü Pascal’ın kumarını geliştirdi.

Bu yaklaşımı geliştirmek için Pascal iki olasılık düşündü. Birincisi, Tanrı vardır. İkincisi, Tanrı yoktur. Sonra, ölümden sonra Tanrı’ya inanmanın ya da inanmamanın sonuçlarını inceledi. Pascal’ın açıkladığı gibi, seçimimiz sonucunda ortaya çıkabilecek esasen dört olası senaryo vardır:
- Biz inanmayı seçiyoruz ve Tanrı var.
- Biz inanmayı seçiyoruz ve Tanrı yok.
- Biz inanmamayı seçiyoruz ve Tanrı var ve
- İnanmamayı seçiyoruz ve Tanrı yok.
Eğer Tanrı varsa ve ona inanıyorsanız, cennete gidersiniz; inanmıyorsanız cehenneme. Öte yandan, Tanrı yoksa, inançlı olun ya da olmayın, hiçbir şey olmaz. Pascal’a göre en akıllıca strateji Tanrı’ya inanmaktır. En iyi ihtimalle cennete gidersiniz; en kötü ihtimalle hiçbir şey yaşanmaz. Buna karşılık, Tanrı’ya inanmazsanız, en kötü durumda cehenneme gidebilirsiniz.
Pascal’ın düşünceleri anlaşılırdır; ancak dini metinlere dayalı senaryoları referans alır ve üstün bir varlığın varlığını kanıtlamaz. Pascal, Tanrı’ya inanmanın matematiksel açıdan mantıklı olduğunu savunur.

Varlığın doğasını ele alan ontolojik yaklaşımlar ise daha ikna edici görünür. Theolog ve filozof Anselm of Canterbury (1033–1109) bu fikirleri geçen binyılın başında ortaya koydu. Anselm, Tanrı’yı, kendisinden daha yüce bir şeyin düşünülemeyeceği bir varlık olarak tanımladı.
Eğer Tanrı yoksa, o zaman daha yüce bir şey hayal etmek mümkün olurdu: var olan ve en yüce özelliklere sahip başka bir varlık. Ancak bu düşünce çelişkili olurdu, çünkü en yüce şeyin ötesinde başka bir şey olamaz. Bu nedenle, Tanrı’nın var olmadığı varsayımı yanlış olmalıdır.
Onotolojik Yaklaşıma Göre Tanrı’nın Varlığı
Bu fikrin tekrar ele alınması, Descartes’ın (1596–1650) çalışmalarıyla mümkün oldu. Descartes, görünüşe göre Anselm’in yazılarından habersizdi, ancak Tanrı’nın varlığı için neredeyse aynı mantıksal yapıyı kullandı. Birkaç on yıl sonra Leibniz (1646–1716) bu yaklaşımı inceledi ve eksik buldu.
Ona göre, Descartes “mükemmel özelliklerin” birbiriyle uyumlu olduğunu göstermemişti. Leibniz, mükemmelliğin doğrudan araştırılamayacağını savundu. Dolayısıyla, mükemmel özelliklerin tek bir varlıkta birleşemeyeceğini kanıtlamak imkânsızdı. Bu nedenle, ilahi bir varlığın mümkün olduğu kabul edilmeliydi. Anselm ve Descartes’ın fikirlerine dayanarak, Tanrı’nın var olduğu sonucuna varıldı.
Tanrı’nın varlığını matematik yardımı ile kanıtlama çabası ancak matematikçi ve filozof Kurt Gödel’in çabalarıyla bir anlam kazandı. Gödel bu konuyu 25 yaşındayken kafasına takmıştı. Sonunda Gödel, Tanrı’nın varlığını göstermek için matematiksel bir kanıt geliştirdi.

Gödel, matematikte doğruluğu kanıtlanamayan ifadelerin her zaman var olduğunu göstermişti. Bunu yaparken mantıktan yararlanmıştı. Aynı mantık yaklaşımı, onu Tanrı’nın varlığını kanıtlamaya da yönlendirdi. Şimdi, aksiyomlar (Ax), teoremler (Th) ve tanımlamalardan (Df) oluşan 12 adımlık bu sürece bakalım.
Kurt Gödel’in Tanrı’nın Varlığına Dair İspatı
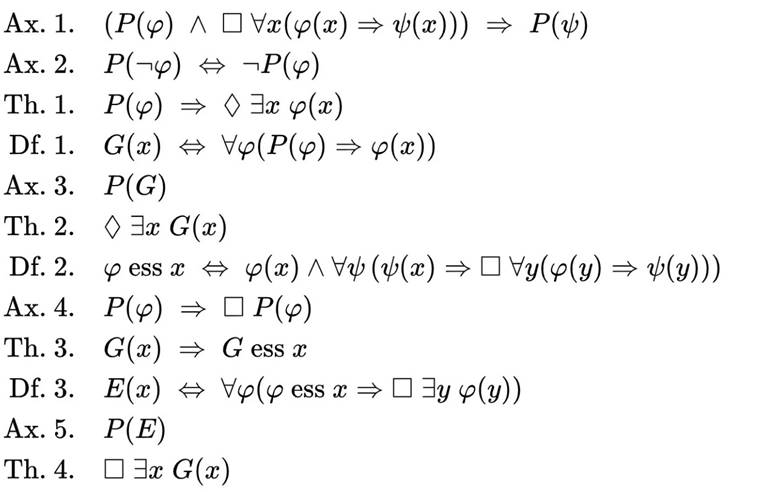
Gödel’in düşünce akışını adım adım takip etmek mümkündür. Başlangıçta bir aksiyomla, yani bir varsayımla yola çıkar: Eğer φ, P özelliğine sahipse ve φ’den her zaman ψ sonucu çıkıyorsa, o zaman ψ de P özelliğine sahiptir. Basitleştirmek için, P’nin “pozitif” anlamına geldiğini varsayabiliriz.
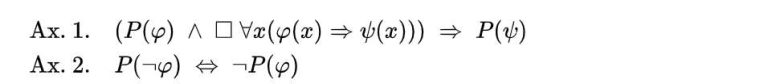
İkinci aksiyom, P için daha net bir çerçeve çizer. Bir şeyin zıttı pozitifse, o şeyin kendisi negatif olmalıdır. Böylece Gödel, dünyayı siyah ve beyaz olarak ikiye ayırır: Bir şey ya iyidir ya da kötüdür. Bu iki önermeden yola çıkarak Gödel ilk teoremini türetir. Eğer φ pozitif bir özellikse, φ özelliğine sahip bir x var olma olasılığına sahiptir.

Burada matematikçi ilk kez ilahi bir varlık tanımına yönelir. Bir x, tüm pozitif özelliklere φ sahip olduğunda ilahi olur.. İkinci aksiyom sayesinde, böyle tanımlanan bir Tanrı’nın negatif özelliklere sahip olması mümkün değildir.
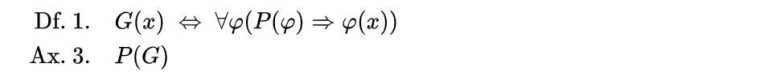
Üçüncü aksiyom, ilahiliğin kendisinin pozitif bir özellik olduğunu belirtir. Bu, tartışmaya açık bir nokta değildir. İkinci teorem şimdi daha somut hale gelir. Üçüncü aksiyom ve birinci teorem birleştirildiğinde, ilahi bir varlık x’in var olması mümkün olur.

Gödel’in sonraki adımlardaki amacı, kurduğu bu çerçeve içinde Tanrı’nın zorunlu olarak var olduğunu göstermek olur. Bunun için ikinci bir tanım getirir: x nesnesinin “özünü” φ olarak tanımlar.
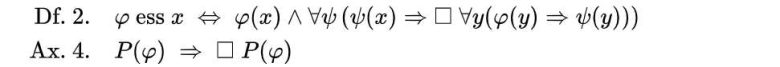
Bu noktada Gödel üçüncü teoremini formüle eder: Eğer bir varlık x ilahiyse, o zaman ilahilik onun temel özelliğidir. Bu mantıklıdır, çünkü ilahi bir varlık tüm pozitif özelliklere sahiptir ve bu da x’in özelliklerini sabitler.

Sonraki adım, belirli bir varlığın varlığıyla ilgilidir. Eğer bir yerlerde, en az bir varlık y, x’in temel özelliği olan φ özelliğine sahipse, o zaman x de vardır. Beşinci aksiyoma göre, varlık da pozitif bir özelliktir. Bu noktadan itibaren, Tanrı’nın var olduğu sonucuna ulaşılır. Çünkü bu varlık her pozitif özelliğe sahiptir ve varlık da pozitif bir özelliktir.

Tanrı’nın Varlığını Matematik Yardımı İle Çözme Girişimi İle İlgili Sorunlar
Gödel son derece dindar biri idi. Ontolojik kanıtını yanlış kurmuş olabileceğinden ya da kendisinin yanlış anlaşılmasından korktuğu için kanıtını hayattayken yayınlamamıştı. Gerçekten de Gödel’in detaylarını kısaca size aktardığımız ispatı birtakım eleştirilere maruz kalmıştır.
Sonuç olarak, Gödel’in mantıksal çıkarımları doğrudur; bilgisayarlar bile bu zinciri doğrulamıştır. Ancak yine de eleştiriler yapılmıştır. Özellikle aksiyomlar sorgulanabilir durumdadır. Örneğin, neden dünya mutlaka “iyi” ve “kötü” olarak ikiye ayrılmak zorunda olsun? Ayrıca Gödel, pozitif bir özelliğin tam olarak ne olduğunu da ayrıntılı şekilde açıklamamıştır.

Yıllar boyunca birçok kişi, Tanrı’nın varlığını kanıtlamak için matematiği kullanmaya çalıştı. Ancak henüz bunu başaran olmadı. Matematiğin böyle bir kanıt sunup sunamayacağı ise temelden tartışmalıdır. Yine de, matematiğin böylesine beklenmedik alanlarda karşımıza çıkması oldukça heyecan vericidir.
Kaynaklar ve ileri okumalar:
- Can God Be Proved Mathematically?; Yayınlanma tarihi: 4 Ekim 2022. Bağlantı: Can God Be Proved Mathematically?/
- Benzmüller, Christoph & Woltzenlogel Paleo, Bruno. (2013). Formalization, Mechanization and Automation of Gödel’s Proof of God’s Existence.
- Smith, David. “Pascal’s Wager: Should you Bet on God’s Existence?” TheCollector.com, November 6, 2023, https://www.thecollector.com/pascals-wager-god/.
Matematiksel





