Suç mahallindeki kan lekeleri, orada neler olup bitiği hakkında bize birçok ipucu verir. Kan Lekesi Desen Analizi (Bloodstain Pattern Analysis: BPA) suç mahallindeki kan lekelerine neden olan unsurları yeniden yaratmak için kan lekelerini yorumlar. Biyoloji, fizik ve matematik; kanın kaynağını saptamada, kurbanın ve failin pozisyonlarını belirlemede yardımcı olur.

Sayısız film ve TV dizisi sayesinde bir olay yeri soruşturmasının nasıl yapıldığını az çok biliyoruz. Peki size olay yeri soruşturması yapılırken matematikten yararlanıyoruz desem ne düşünürsünüz? “Ama matematik ne işe yarayacak ki?” demiş olabilirsiniz. Ancak az bilinmesine rağmen gerçek şu ki, okulda öğrendiğimiz neredeyse tüm matematik suçların ardındaki gizemi çözmekte işe yarar. Bu yazımızda temel trigonometrinin bu bağlamda nasıl kullanıldığını keşfedeceğiz.
Kan Lekesi Analizi Bize Suçun Nerede İşlendiğini Nasıl Söyler?
Kanın kaynağını ve mağdur ile failin pozisyonlarını belirlemek için biyoloji, fizik ve matematik birlikte çalışır. Bıçaklanma, darp ve silahla yaralanma vb. gibi herhangi bir olay sonucunda iki tür kan lekesi oluşacaktır. Bunlara etki ve pasif lekeler denir. Etki lekeleri, havadan yansıyan kan sonucu oluşur. Pasif lekeler ise yerçekiminin etkisi sonucu yani damlama sonucunda oluşur.
Kan lekeleri yüzeye çarptığında oluşan kan lekelerinin şekli, etki açısına ve kat edilen mesafeye bağlıdır. Kan lekesinin şekli ve kuyruğu, kanın ne yöne gittiğini gösterir. Aşağıdaki diyagramda gösterildiği gibi yerde üç kan damlası hayal edelim. (Mesela başından vurulmuş birinin kanı)
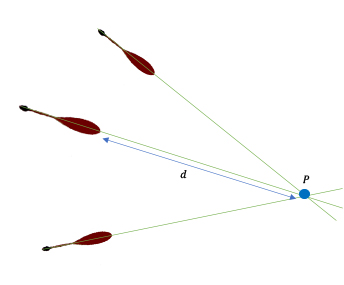
Şimdi de kan lekelerinden kat ettikleri mesafeye göre çizgiler hayal edelim. Bu çizgiler bir P noktasında kesişiyorlar. Kanın gerçek kaynağı (mesela başından vurulmuş kişinin başı) bu P noktasından dikey olarak yukarıda olacaktır. Tam olarak ne kadar yukarıda olduğunu bulmak için ise biraz geometriye ihtiyacımız var.
Eğer kan düz bir zemine düşüyorsa kanın yörüngesi zemine 90 derecelik bir açı yapar ve böylece dairesel şekilli bir damlacık oluşturur. Eğer kan zemine eğik olarak yaklaşık 70 dereceden daha küçük bir açıyla düşerse kuyruğu olan eliptik bir şekil oluşturur.

İndinans Açısı
Olay yeri inceleme ekibi kan lekesi analizi esnasında, kan lekesinin boyunu a, enini b olarak ölçmüş olsunlar. Ekip daha sonra aşağıdaki diyagramda gösterilen dik üçgeni kullanarak insidans açısı olarak adlandırılan düşen kan damlasının yüzeyle yaptığı açıyı hesaplayabilirler.
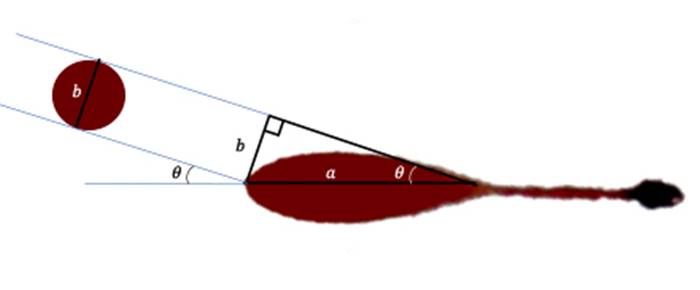
Diyagramda da görüldüğü üzere kan damlası, insidans açısı Θ’ya eşit olan bir yüzeye doğru ilerler. Damlacığın çapını enine eşit, yani b olarak kabul edelim. (Bu, gerçekte pek doğru olmayabilir ancak iyi bir yaklaşım yapmamızı sağlar.) Çapı da gösterildiği gibi taşıyacak olursak dik açılı bir üçgen oluşturabiliriz. Eni b, bu üçgende karşısındaki açı Θ ve boyu, a, hipotenüstür. Dolayısıyla; sinΘ=b/a olacaktır. Sonucunda a ve b’ yi kan lekesinden ölçtüğümüz için şimdi Θ’yı sin-1(b/a)= Θ olarak bulabiliriz.
Kaynağın Yüksekliği
Şimdi kan lekelerinin kaynağının yüksekliğini hesaplamaya hazırız. Kenarları daha önce tanımladığımız P noktasında kesişen çizgilerden oluşan dik açılı bir üçgen çizelim. P noktasında zemine dik açıyla yükselen çizgi ve kan lekesinden başlayan çizgi zeminle Θ açısını yapıyorlar.
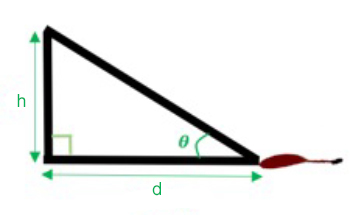
Dik çizginin yüksekliği olan h şöyle veriliyor: h/d= tan (Θ). Buradan da h= d. tan (Θ) sonucunu elde edebiliriz. Θ’nın değerini ve uzaklık d’yi bildiğimiz için (ilk görsele bakabilirsiniz) kaynağın yüksekliği olan h’yi bulabiliriz. Örneğin, kurbanın başından vurulduğunu zaten biliyorsanız bu bilgi size kişinin olay esnasında ayakta olup olmadığını ya da yerde uzanırken darbe alıp almadığını gösterecektir.
Kısaca aktardığımız gibi kan lekesi desen analizi çıktıları, laboratuvar bulgularını veya tanık ifadelerini doğrulamada kullanılabilir. Şaşırtıcı bir şekilde trigonometri gibi temel bir şey bize suç mahallinde ne olduğu hakkında çok şey söyleyecektir. Daha fazlası için: Adli Bilimler Suçluları Yakalamada Matematikten Nasıl Faydalanır?
Kaynaklar ve ileri okumalar:
- Solving crimes with maths: Bloodstain pattern analysis.Yayınlanma tarihi: 22 Kasım 2021; Kaynak site: Plus Maths. Bağlantı: Solving crimes with maths: Bloodstain pattern analysis/
- Moza, Bhavika & Mukherjee, Debhjit & Verma, Priyanka. (2023). Blood Stain Pattern Analysis. A Comprehensive Review of Methods, Reliability of Computerized Analysis, and Future Advancements. 1. 5-10. 10.5281/zenodo.8213482.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










