Suçla mücadele gibi bir başlık ile matematik arasında bir ilişki olabileceği elbette kolay kolay akla gelmeyecektir. Sonuçta herhangi birine matematik hakkında düşüncelerini sorsanız, sıkıcı ve zor olduğunun yanı sıra gerçek hayatta bunlar benim işime yaramaz ki sözlerini duyarsınız. Ancak elbette yanılıyor.
Okulda öğrendiğimiz neredeyse tüm matematik suçların ardındaki gizemi çözmekte işe yarar. Polisler bir suçla mücadele ederken birçok zorlukla karşı karşıyadır. Suç veya kaza mahallinde neler olduğunu bulmaları gerekir. Bilgi için saklanması ve çıkarılması gereken kafa karıştırıcı verileri yorumlamaları gerekir.
Suç mahallinde kalan tüm kanıtlara bakmalı ve ne olduğunu ve kimin yaptığını anlamak için geriye doğru çalışmalılar. Çoğu zaman kanıtlar, iyi anlaşılan fiziksel bir sürecin sonucudur. Yani ortada bir sonuç vardır ve başlangıç koşullarının tahmin edilmesi gerekmektedir.
Matematik Yardımı İle Kaçan Arabayı Yakalayalım
Diyelim ki bir polis departmanında çalışıyorsunuz ve bir banka soygunu haberi alıyorsunuz. Soyguncu arabayla kaçmasına rağmen polis tarafından takip edildi. İyi haber şu ki polis arabanın plakasının fotoğrafını çekmeyi başardı ama kötü haber şu ki fotoğraf bulanık.

Plakanın daha net bir resmini elde etmek için bulanıklaştırma sürecini matematiksel olarak modelleyebiliriz. Bu sayede de bulanıklığın bir kısmını ortadan kaldırmak mümkün olur. Bunun için kullanılan bir fonksiyon vardır. Fonksiyonun denklemini aşağıda görebilirsiniz.
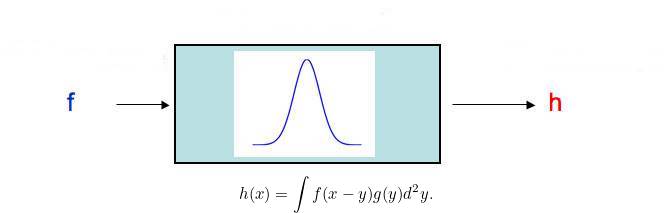
Fonksiyondaki x görüntüdeki piksel sayısını ifade eder. Her pikselin, rengi ve parlaklığı hakkında bilgi veren piksel değeri adı verilen kendine ait bir numarası vardır. f(x) fonksiyonu bulanıklaşmadan önceki her pikselin x piksel değerini verir. h(x) ise aynı biçimde resim bulanık hale geldikten sonraki değeri belirler. Yukarıdaki formülü geriye doğru çalıştırmak bize f(x) tarafından verilen bulanık olmayan görüntüyü verecektir.
Gördüğünüz gibi televizyon dizilerinde görmeye alıştığımız şeyler aslında kurgu değil. Bunun için polis teşkilatının elindeki en güçlü silah matematiktir. Sadece bu kadar da değil. Adli bilimler de matematiksel ve fiziksel kanıtları dikkate alır. Sayısız film ve dizi bize olay yeri incelemesinin önemini öğretti. Ancak daha az bilinen şey, matematiğin bunda önemli bir rolü olduğu gerçeğidir.
Bir suçun nerede işlendiğini kan lekeleri bize söyleyebilir mi?
Kan lekeleri, suç mahallinde ne olduğu hakkında birçok ipucu barındırır. Kan lekesi desen analizi (BPA), kan lekelerine neden olan eylemleri yeniden oluşturmak için bir suç mahallindeki kan lekelerinin yorumlanmasıdır.
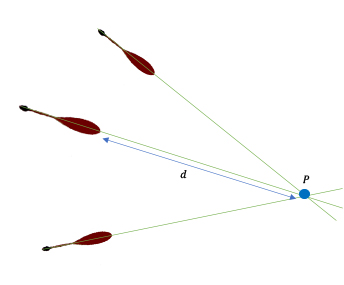
Kanın kaynağını ve mağdur ile failin pozisyonlarını belirlemek için biyoloji, fizik ve matematik birlikte çalışır. Kan lekesinin şekli ve kuyruğu, kanın hareket ettiği yönü gösterir. Aşağıdaki şemada gösterildiği gibi, yerde üç kan lekesi olduğunu hayal edin. Ayrıca tüm bu lekelerin aynı kaynaktan geldiğini düşünün. Şimdi kan lekelerinden hareket yönlerine göre çizgiler çizdiğini hayal edin. Bu çizgiler kaynağınız olan P noktasında buluşacaktır.
.
.
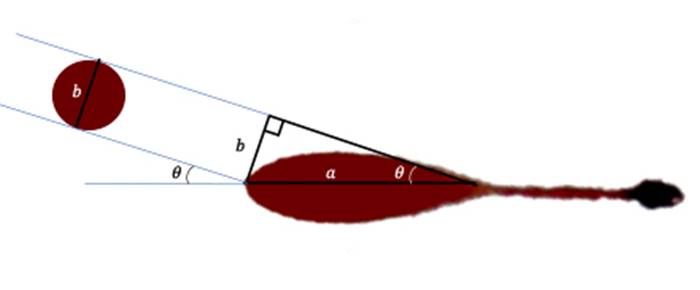
Kaynağı bulduktan sonra tam olarak hangi yükseklikte olduğunu bulmak için biraz daha geometri yapmak gerekir. Damlacıklar bir yüzeye çarptığında oluşan şekil aşağıda da gördüğünüz gibi çarpma açısına ve kat edilen mesafeye bağlıdır. Öncelikle yapılması gereken kan damlasının yüzeye çarptığı açıyı belirlemektir.

Uzmanlar bu açıyı belirlemek için aşağıda gördüğünüz uzunlukları hesaplar. Sonrasında da kan damlasının yüzeye çarptığı açıyı bulmaya çalışır. Hesaplamada çarpmadan önceki bir damlacık çapının çarptıktan sonrakine eşit olduğu varsayılır. Bu tam olarak doğru olmasa da bize yaklaşık bir cevap verecektir. Bundan sonra yapılması gereken dik üçgenler ve trigonometrik bağlantılar yardımı ile kanın geliş açısını hesaplamaktır.
Kan örneği analizi ile üretilen çıktılar, tanık ifadelerini ve laboratuvar bulgularını doğrulamak için kullanılabilir. Trigonometri gibi basit bir şeyin bize suç mahallinde ne olduğu hakkında çok şey anlatabilmesi şaşırtıcıdır. Ancak adli bilimlerin matematik ile kesiştiği tek yer burası değildir.
Değişimler
Üstel ve logaritmik fonksiyonlar da adli tıpta önemli bir rol oynar. Üstel fonksiyon, zaman değiştikçe mevcut malzeme miktarına bağlı olan süreçlerle ilgilidir. En önemli kullanım yerlerinden biri ölüm zamanını hesaplama ile ilgilidir. Adli bilim yaklaşık bir ölüm zamanını belirlemek ve oluşturmak için vücut sıcaklık verilerini kullanır. Ölümden sonra vücut, çevre sıcaklığına ulaşana kadar soğur. Newton’un soğuma yasası aracılığıyla azalan ısıyı matematiksel olarak modellediğimizde karşımıza üstel bir fonksiyon çıkacaktır. Ancak daha bitmedi…
Coğrafi Profilleme
Bazen işlenen bir dizi suç birbiri ile bağlantılı olur. Bu tip bir cinayeti aydınlatmak için genellikle, bağlantılı suçların her birinden önce bilgiler alınır. Daha sonra bu bilgiler ve önceki sabıka kayıtlarından yola çıkarak bir şüpheli listesi yapılır. Coğrafi profilleme birbiriyle ilişkili suç bilgilerinden faydalanarak muhtemel sanık adresine ulaşmak için kullanılan bir araştırma yöntemidir.
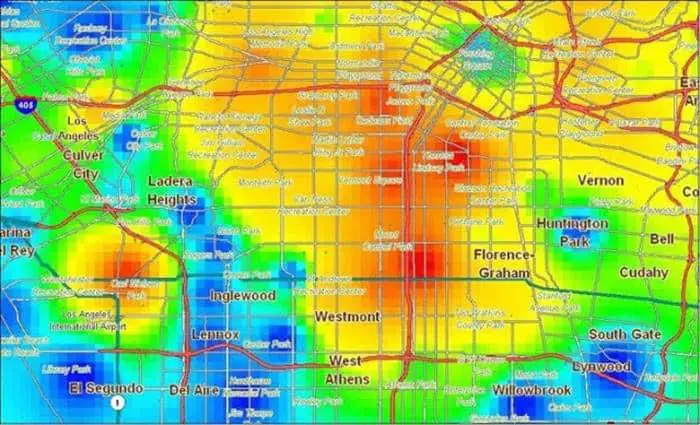
Suçluların aşina oldukları alanlarda hareket etme eğiliminde oldukları gerçeğine dayanarak her şüpheliye bir olasılık atamak için bağlantılı suçların mekânsal kalıplarını analiz etmeyi içerir. Sistem sayesinde suç işlenen yerden yola çıkarak muhtemel suçlu ikametinin haritası oluşturulur. Bu sayede her şüpheliyi araştırmak için zaman ve kaynak harcanmaz. Bunun yerine, olası suçlular coğrafi profillemeyle elde edilen olasılığa göre sıralanır.
Olasılık ve İstatistik
Olasılık ve istatistik de günümüzde suç ile ilgili araştırmalarda giderek daha fazla kullanılmaktadır. İstatistiksel analiz aracılığı ile benzerlikler ve farklılıklar belirlenebilmektedir. Sonuçta iki kişinin aynı DNA profillerine sahip olma şansı yüz trilyonda birdir. Ayrıca adli tıp biyologları çoğu zaman küçük bir alanda ve genelde bozulmuş olay yeri örnekleriyle çalışmak zorunda kalır. Bu, bir bireyin tanımlanmasını zor hale getirir. Bunun sonucunda da çıkarımlar yapmak için ince olasılıklı argümanlar gerekir.
Parmak izi, kan grubu ve DNA ile ilgili kanıtlar analiz edilirken özellikle koşullu olasılık devreye girer. Bu tür değerlendirmeler, bir suçla ilgili iki olayın bağlantılı veya bağımsız olup olmadığını belirlemeye yarar. Koşullu olasılığa önem verilmemesi, hatalı çıkarımlar yapılmasına neden olur.
Sonuç olarak, okulda öğrendiğimiz matematik ile ilgili hemen hemen her konu, adli bilim tarafından suçluları yakalamak için bir biçimde kullanılmaktadır. Matematik ne işime yarar ki diye soranlara sevgilerimizle…
Yazının devamında ayrıca göz atmak isterseniz: Ya Katillerin Bir Suçu Yoksa? Seri Katil Geni Diye Bir Şey Gerçekten Var mı?
Kaynaklar ve ileri okumalar:
- Catching criminals with maths; Yayınlanma tarihi: 24 Kasım 2016. Kaynak site: Chalk dust magazine. Bağlantı: Catching criminals with maths
- Solving crimes with maths: Bloodstain pattern analysis; Yayınlanma tarihi: 22 Kasım 2021. Kaynak site: Plus Math. Bağlantı: Solving crimes with maths: Bloodstain pattern analysis/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










