
Ağırlık merkezi kavramı makine, bina ve aletlerin tasarımında çok önemli bir yere sahiptir. Örneğin bir otomobili tasarlarken bunu hesaba katmak gereklidir. Aksi takdirde araba dengesiz olacaktır. Bunun sonucunda da virajlarda kolayca savrulacaktır. Basit bir yemek kaşığı bile bu bilgi hesaba katılarak tasarlanmaktadır. Aksi taktirde kaşığın tutuşu sizi asla konforlu hissettirmez.
Ağırlık Merkezi Nedir?
Tanımı ilk olarak eski Yunan fizikçi, matematikçi ve mühendis olan Arşimet tarafından kullanılmıştır. Yer çekimiyle ilgili varsayımları basitleştirmek için çalışmıştır. Sonuç olarak da şu an kullandığımız ağırlık merkezi denilen matematiksel özelliğe ulaşmıştır.
Ağırlık merkezi yerçekimine bağlıdır ve vektöreldir. Bu nokta tüm şeklin yerçekimine göre mükemmel bir biçimde dengelendiği noktadır. Tam o yere yerçekiminin tersi yönünde destek verilirse, nesne dengede duracaktır. Yani bu noktadan asılan cisim, dengede kalır. Örneğin bir cetvel tam ortasından asıldığında mutlaka yatay konumda kalmak zorunda değildir. Nasıl bırakılırsa öyle kalır. Yani eğik bırakılırsa eğik, dikey bırakılırsa dikey kalacaktır.

Kütle Merkezi Nedir?
Kütle merkezi ve ağırlık merkezi kavramları ilk bakışta aynı şey gibi görünebilir. Bu iki kavram ilişkili olsalar da aynı şey değiller. Aralarındaki fark aslında kütle ile ağırlık arasındaki farktan kaynaklanmaktadır. Kütle bir cisimdeki madde miktarıdır. Ağırlık ise bir cisme kütlesinden dolayı uygulanan yerçekimi kuvvetidir.
Bu nedenle kütleden bahsederken kilogram birimini, ağırlıktan bahsederken kuvvetin birimi olan Newton’u kullanırız. Yerçekimi olsa da olmasa da cisimlerin kütlesi hep vardır. Kütle merkezi, cismin kütlesinin tamamının toplandığı kabul edilen bir noktadır. Ancak dünyada yaşadığımıza ve yerçekimi olduğuna göre yazının devamındaki örneklerde ağırlık merkezi ile kütle merkezini aynı şey olarak kabul edebilirisniz.
Sporcular için büyük önemi vardır.
Bir cisme baktığımızda beynimiz otomatik olarak yerini tahmin eder ve pozisyonunu bu bilgiye göre ayarlar. Örneğin, bize doğru yaklaşmakta olan bir cismi tutacaksak onun ağırlık merkezine doğru elimizi uzatırız. Güreşçiler rakiplerinin ağırlık merkezine göre güçlerini ayarlarlar. Hatta bütün dikkatlerini buna verirler.

Künde pozisyonuna gelmiş bir sporcu, bu sayede tuş olmaktan kurtulabilir. Bu amaçla kol ve bacaklarını açar ve bedenini iyice yere bastırır. Böylece ağırlık merkezini yere yaklaştırmış olur. Ne kadar aşağıda olursa, o kişiyi yere yıkmak o denli güç olur. Bu duruma piramidi örnek verebiliriz. Piramit, ağırlığının çoğu aşağıda toplanmış ve üstelik de tabanı geniş bir cisimdir. Bu nedenle güreşçiler dengelerini korumak için sık sık piramit pozisyonu alırlar.
Algılarımız üzerinde önemli bir etkisi vardır.
Şaşırtıcı ama gerçekten de bu noktanın algılarımız üzerinde psikolojik etkileri vardır. Bir cisme baktığımızda beynimiz cismin görünümünden ve şeklinden hem ağırlığını hem de ağırlık merkezinin yerini tahmin eder. Beynimiz, genellikle bu merkezin cismin daha büyük parçasına yakın olduğunu tecrübelerinden bilir. Buna aykırı bir durumla karşılaştığında şaşırıp yanlış tepki verir. Aşağıdaki cismin ağırlık merkezi sizce hangi noktaya yakındır?
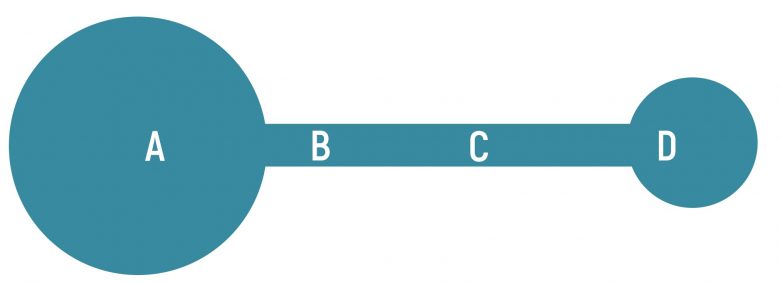
Birçok insanın bu soruya “B” diye yanıt vereceğini tahmin edebiliriz. Eğer bu cismi tutmamız gerekirse, genellikle B noktasını tercih ederiz. Görüldüğü gibi insan beyni bir cisim ya da sistemin ağırlık merkezini tahmin etme yeteneğine sahiptir. Bu yeteneğini çocukluğunda çeşitli cisimlerle oynayarak, deneyimle kazanmıştır. Şimdi aynı soruyu aşağıdaki cisim için soralım.
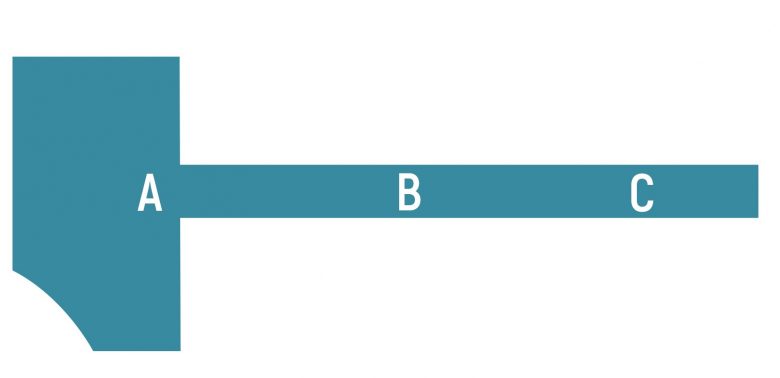
Bu kez cevabınızın “A” olduğunu tahmin ediyoruz. Şekil bir çekice benzediği için, beynimiz otomatik olarak A kısmının demirden yapıldığını, bu nedenle de ağırlık merkezinin buraya yakın olması gerektiğini tahmin etmiştir. A noktasının tercih etmemizde, şekil ve cismin yapıldığı malzeme bilgisi bizi yönlendirmiştir. (Demir parça daha ağır olmalı…)
Güvenlik açısından önemi vardır.
Eşya ve araçların tasarımında olağanüstü önemi vardır. Örneğin bir kılıcın sapında değil bıçağında olmalıdır ki daha büyük bir güçle kesebilsin. Bir insanın ki kalça kemiklerinin içinde olmalıdır ki rahat yürüyebilsin. (Hamile kadınların yürümekte zorlanmasının nedeni, şişen karınları nedeniyle ağırlık merkezlerinin öne doğru kaymasıdır.)
Bir otomobilin ki olabildiğince ortada ve aşağıda olmalıdır ki virajlara rahat girebilsin ve kolayca devrilmesin. Bu nedenle elektrikli Tesla otomobillerinin en ağır parçası olan piller, aracın tabanına yerleştirilmiştir. Otomobillerde genelde motoruna yakındır. O halde motoru önde olan araçlarda, bu merkez öne doğru kayar. Ortaya çekebilmek için cismin arka bölümü uzatılır.
Ergonomik önemi vardır.
Şimdi şu soruyu soralım. Fincan ve Çanta: Hangisini taşımak daha kolay?
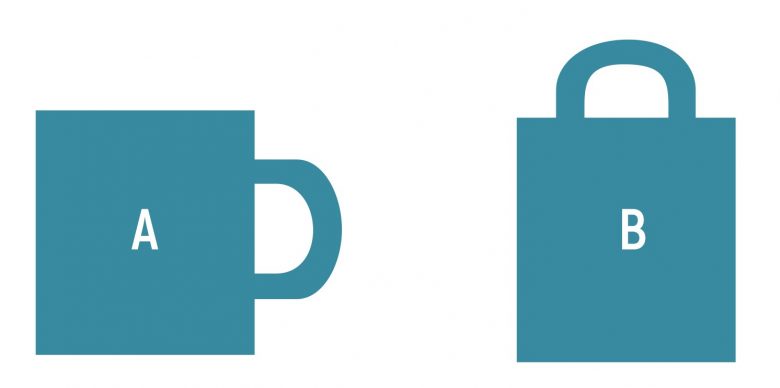
Elbette ki “B” cismini taşımak daha kolaydır. Nedeni, B cisminin ağırlık merkezinin tutuş noktasından yani sapından geçmesidir.
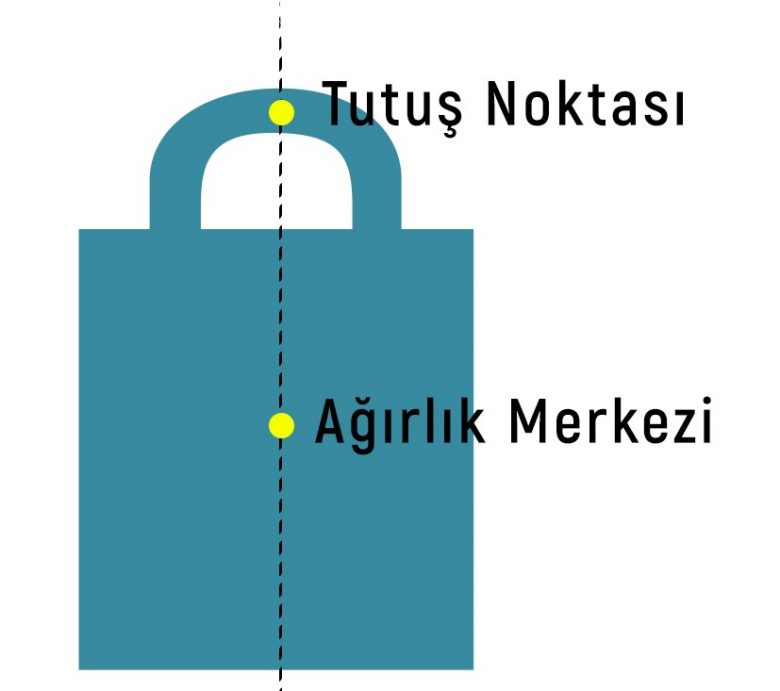
Diğer cismin ağırlık merkezi ise tutma noktası (kulp) bir hizada değildir. Bu nedenle bu cismi taşımak zor, ancak içindeki sıvıyı boşaltmak kolaydır. Çünkü bu cisim ağırlık merkezine doğru dönme eğilimindedir.
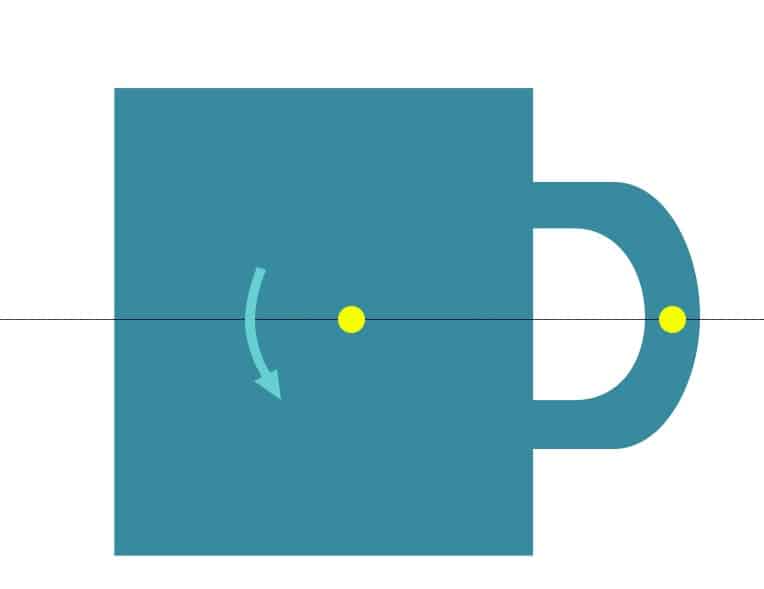
Görüldüğü gibi en basit bir cismin tasarımında bile bu merkezin konumunu göz önünde bulundurmamız gerekiyor. Bu, özellikle modern ve bilimsel tasarım için çok daha önemli olacaktır.
Simetrik cisimlerin ağırlık merkezi, simetri merkezidir.
Ağırlık merkezi çubukların tam ortasıdır. Çemberde ise merkezdedir. Kare ve dikdörtgenlerde köşegenlerinin kesim noktasıdır. Homojen bir maddeden yapılmış olan bir doğru parçasında tam ortasıdır. Kare, dikdörtgen, daire ve kürenin bu şekillerin tam ortasıdır; çünkü bu cisimler simetriktir. Simetrik olmayan üçgende ise tabana yakındır; çünkü tabanı daha geniştir.
Bu yazının devamında göz atmak isterseniz: Telefonunuz Data ile Doluyken Daha mı Ağırdır? Gelin Hesaplayalım!
Kaynaklar ve ileri okumalar
- Difference between Center of Mass and Center of Gravity. Yayınlanma tarihi: 23 Mayıs 2022; Bağlantı: https://www.geeksforgeeks.org/
- Centre of Gravity; Yayınlanma tarihi: 10 Ekim 2010; Bağlantı: https://esfsciencenew.wordpress.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










