Matematiksel Platonizm ya da Platonculuk, matematiğin doğasına dair en eski ve en etkili yaklaşımlardan biridir. Bu yazıda, öncelikle genel anlamda Platonculuğun ne olduğunu ve matematikle ilişkisini inceleyeceğiz. Daha sonra, bu görüşün en güçlü savunucularından biri olan Frege’nin Matematiksel Platonculuk argümanını ele alacağız.
Matematiksel Platonculuğun Temel İddiası
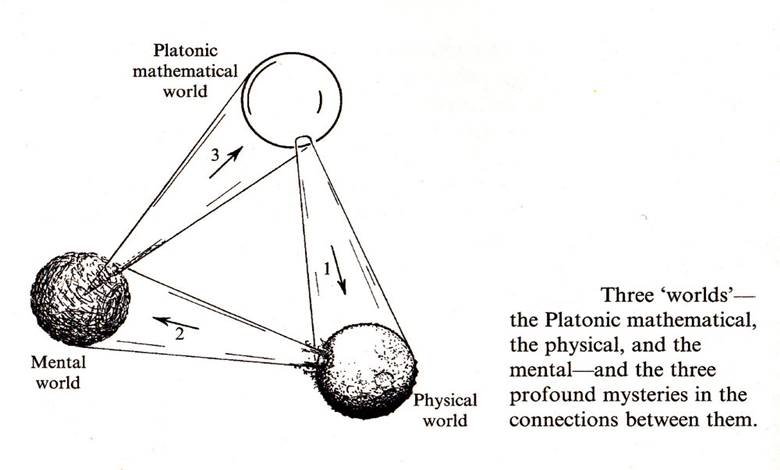
Matematiksel Platonculuk, matematiksel nesnelerin insan faaliyetinden, düşüncesinden ve dilinden bağımsız olarak var olduğunu savunur. Bu nedenle, matematiksel nesnelerin insanlar tarafından inşa edilmek yerine keşfedildiğini öne süren bir görüştür.
Burada “matematiksel nesne” terimi herhangi bir teknik veya karmaşık bir şeyi ifade etmez; matematiksel terimlerle tanımlanabilen her şeyi kapsar. Bu görüş ilk bakışta oldukça basit görünebilir, ancak aslında oldukça derindir. Çünkü bir şeyin keşfedilmesi ile insan tarafından yaratılması arasındaki fark net değildir.

Özellikle kavramsal nesneler söz konusu olduğunda, keşfetme ve yaratma arasındaki ayrım daha da belirsizleşir. Matematikçilerin ilgilendiği nesneler de büyük ölçüde kavramsal olduğu için bu tartışma daha da karmaşık hale gelir.
Matematiksel Platonculuk, aynı zamanda bir metafizik doktrin olması nedeniyle daha da karmaşık hale gelir. Metafiziğin tam olarak ne olduğu tartışmalı bir konu olsa da, genel anlamda evrenin ve varlıkların gerçek doğasını inceleyen bir alan olarak tanımlanır. Metafizik, şeylerin gerçekte nasıl olduğunu araştırırken, bilginin koşullarını ve nasıl elde edildiğini sorgulayan epistemolojiden farklı bir yaklaşım benimser.
Matematiksel Platonculuğun Sonuçları
Matematiksel Platonculuğu benimsemenin birçok sonucu vardır, ancak bunlardan en önemlisi, fizikselci dünya görüşü üzerindeki etkisidir. Fizikselcilik (physicalism), dünyayı yalnızca fiziksel olgularla açıklayabileceğimizi savunan görüştür.
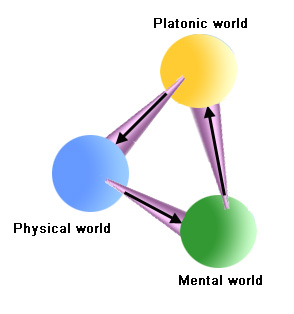
Ancak, Matematiksel Platonculuk matematiksel nesnelerin gerçek olduğunu iddia eder ve matematiksel nesnelerin fiziksel değil, kavramsal olduğu düşünüldüğünde, bu görüş fiziksel olmayan olguların da gerçekliğin tam bir açıklamasına dahil edilmesi gerektiğini ima eder.
Matematiksel Platonculuk özellikle güçlü bir görüştür, çünkü matematiğin en tutarlı, en bilimsel ve en güvenilir bilgi üretim alanı olduğu kabul edilir. Son olarak, bu felsefi akım adını Platon’dan alsa da, Platon’un matematik hakkındaki görüşleriyle doğrudan bağlantılı değildir.
Platonculuk, yalnızca matematiğe özgü olmayan daha genel bir kavramdır ve bir şeyin bizden bağımsız olarak var olduğunu öne süren bir düşünce biçimidir. Günümüzde kullanılan “Platonculuk” kavramı, Platon’un bizzat savunduğu görüşlerden farklı alanlara da uygulanmaktadır.
Frege’nin Matematiksel Platonculuk Argümanı

Matematiksel Platonculuğa dair en çok tartışılan argümanlardan biri, Platon’dan değil, Gottlob Frege’den gelmektedir. Frege, günümüzde en etkili matematikçilerden, mantıkçılardan ve dil filozoflarından biri olarak kabul edilir ve onun Matematiksel Platonculuk teorisi de aynı derecede etkileyicidir. Frege’nin argümanı iki temel öncül üzerine kuruludur:
Frege’nin ilk iddiası, matematiksel dilin, gerçek dünyadaki nesneleri tanımlayan doğal dillerle benzer bir yapıya sahip olduğu yönündedir. Örneğin, doğal dillerde “kedi” kelimesi gerçek bir varlığı, yani kedileri temsil eder. Buna benzer şekilde, Frege’ye göre matematiksel terimler de gerçek matematiksel nesneleri temsil eder. Örneğin “2” dediğimizde, bu sadece bir kelime veya sembol değil, gerçekten var olan bir matematiksel nesnedir. Yani, matematiksel nesneler, bağımsız olarak var olurlar.
Frege’nin ikinci argümanı, matematiksel teoremlerin yalnızca sembollerden ibaret olmadığı, gerçekten doğru oldukları görüşüne dayanır. Örneğin, “3 + 2 = 5” ifadesi, sadece bizim anlaştığımız bir kural değildir; matematiksel bir gerçekliği ifade eder.
Frege’nin en büyük katkısı, matematiksel terimlerin ve önermelerin anlamı olduğu ve bu anlamın gerçek matematiksel nesnelere karşılık geldiğini göstermeye çalışmasıdır. Bu, Matematiksel Platonculuğun en güçlü savunularından biri olarak kabul edilmektedir. Matematiğin dil yapısının doğal dillerle benzer işlediği düşüncesi, yalnızca Frege’nin kendine özgü bir görüşü değildir; pek çok filozof ve matematikçi de bu paralelliği kabul eder.
Matematiksel Platonculuğa Yönelik İtirazlar
Matematiksel Platonculuğa yönelik pek çok itiraz vardır. Bunların bazıları yalnızca bu görüşü yumuşatmaya çalışırken, bazıları ise tamamen reddetmeyi amaçlar. Bu itirazlardan biri, filozof Paul Benacerraf tarafından ortaya atılmıştır. Bu itirazın kısa bir özeti şudur:
- Eğer matematikçilerin ulaştığı sonuçlar güvenilir ise, bu güvenilirliği açıklayabilmemiz gerekir.
- Ancak, Matematiksel Platonculuk doğruysa, bu güvenilirliği açıklamak mümkün değildir.
Bu son öncül ilk bakışta nereden çıktığı belli olmayan bir iddia gibi görünecektir. Ancak bu argüman, Matematiksel Platonculuğun matematiksel varlıkları zaman ve mekândan bağımsız varlıklar olarak konumlandırdığı gerçeğine dayanır.
- Eğer matematiksel nesneler uzay ve zamanın dışında var oluyorsa, bizimle hiçbir fiziksel veya nedensel etkileşimleri olmamalıdır.
- Ancak, eğer bizimle hiçbir nedensel ilişkileri yoksa, biz onları nasıl bilebiliriz?
Bu, Matematiksel Platonculuğun en büyük sorunlarından biridir. Eğer matematiksel nesneler insan zihninden tamamen bağımsızsa, onlara nasıl erişiyoruz ve onlar hakkında nasıl bilgi ediniyoruz?
Benacerraf’ın sunduğu bu epistemolojik itiraz, Matematiksel Platonculuğun doğrudan reddedilmesine yol açmaz. Ancak, en azından onun yeniden tanımlanması gerektiğini gösterir. Çünkü matematiğin güvenilirliğini açıklamak için, onun nasıl işlediğini ve matematikçilerin gerçekte ne yaptığını daha iyi anlamamız gerekir.
Kaynaklar ve ileri okumalar
- Platonism in the Philosophy of Mathematics. (Erişim Tarihi: 30.06.2021) https://plato.stanford.edu/
- Bernhart, Frank. (1979). Are Mathematical Objects Ontologically Real? Ideas and Suggestions.
- Mathematical Platonism: Is Mathematics Found or Made? Yayınlanma tarihi: 13 Aralık 2023; Bağlantı: https://www.thecollector.com/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





