Bazı şeylerin kesin öyle olmasını düşünürüz. Örneğin gökyüzü mavidir. Alfabedeki a harfi b harfinden önce gelir. Ayrıca 1 artı 1 de her zaman 2 yapar. Gerçekten öyle mi? Sonucunda 1+1=2 en temel matematiksel eşitliktir. Peki neden 1+1=2 diye sorulsa ne cevap verirsiniz?

1 Artı 1 Neden 2 Yapar?
Çoğumuz böyle bir soru karşısında şaşkına döneriz çünkü 1+1=2 bizim için bir gerçektir (ki öyledir). Bu nedenle de hiçbir zaman onun arkasındaki mantığı veya gerçeğin nasıl ortaya çıktığını bulmaya çalışmayız. Çoğumuz için 1+1=2 bir saptamadır ve 2’nin 1 ‘in ardılı olduğunu ifade eder geçeriz. Ancak bazı kabuller çok da kolay bir biçimde gerçekleşmez.

Aslında bakarsanız apaçık öyle dediğimiz pek çok matematiksel olgu için bu durum geçerlidir. Basit bir örnek vermemiz gerekirse 1+1=2 işleminin ispatı tam 360 sayfadır. Bu ispat matematik adına yazılmış en önemli kitaplardan birisi olan “Principia Mathematica”da yer almaktadır. Bu kitap 1910, 1912 ve 1913’te üç cilt olarak yayınlanmıştır.

Kitabın ilk cildi Bertrand Russell ve Alfred North Whitehead tarafından ortaklaşa yazıldı, ancak sonraki iki kitabın neredeyse tamamı Russell’ın eseriydi. Bu kitabın İngilizce versiyonunu incelemek için bu kaynağı kullanabilirsiniz. Ayrıca ispatın yer aldığı bölümden bir sayfayı da yukarıda görebilirisiniz.
Sizin de fark etmiş olacağınız gibi bu kitap popüler bir bilim kitabına benzememektedir. Kitabın büyük çoğunluğu sembolik bir dil ile yazılmıştır. Ayrıca o dönemde kullanılan sembollerin bazıları günümüzde artık kullanılmamaktadır. 360. sayfada 54.43’te ise 1+1=2 işleminin ispatı yer almaktadır.

Basit Bir İspat Neden Bu Kadar Uzun Sürdü?
Tahmin etmiş olacağınız gibi Principia Mathematica temelde “1 artı 1 neden 2 yapar?” sorusuna bir cevap olarak yazılmadı. Yazarların amacı bundan çok daha incelikliydi. Matematiğin her dalı bazı ispatlar ve kabuller üzerine kuruludur. Bu kabul ve ispatlarda daha önceki ispat ve kabullere dayanır.
Mantığın temelleri, günümüzden 2300 yıldan daha uzun bir süre önce, Aristo tarafından atıldı. Aristoteles’in başarısı o kadar kapsamlı ve etkileyiciydi ki, on dokuzuncu yüzyıla kadar mantıkta nispeten az ilerleme oldu. Mantığa bir sonraki önemli katkı 1879 yılında Alman matematikçi ve mantıkçı Gottlob Frege’den geldi. Onun çalışmaları modern mantığın ve analitik felsefenin başlangıç noktasını oluşturur. Frege’nin başarısı, saf mantıktan matematiksel kanıtlar çıkarma çabasıyla bir işaret sistemi oluşturmuş olmasıydı.

Whitehead ile Russell, bu dev eserde tüm aritmetiksel kavramların saf mantıksal kavramlarla tanımlanabileceğini göstermeye çalıştılar. Böylece aritmetik aksiyomların tamamı, saf mantıksal doğruluklar olan az sayıda temel önermeden çıkmış olacaktı. Bu sayede daha önceki çalışmalarında bulunan paradoks ve çelişki türlerinden kaçınırken, matematiğin tamamını mantıksal aksiyomlardan türetmiş olacaklardı.

Frege bir süre dil felsefesi üzerine çalıştıktan sonra, aritmetik yasalarını mantığa uyarlamaya çalıştı. Tüm çelişkileri ortadan kaldıracak biçimde matematiğin ilkelerini aritmetik ve mantıktan türetmek için titiz bir çalışmaya girişmişti.
Bertrand Russell de matematiğin ilkelerini kurma konusunda çalışıyordu. Ayrıca Frege’nin çalışmalarını da yakından takip ediyordu. Ancak çalışmaları esnasında Frege’nin düşünme biçiminde bir hata buldu. Bu hata, Frege’nin deyişiyle, tüm yaşantısını adadığı çalışmanın temelini yok etmişti. Günümüzde bu hatayı Russell Paradoksu olarak biliyoruz.
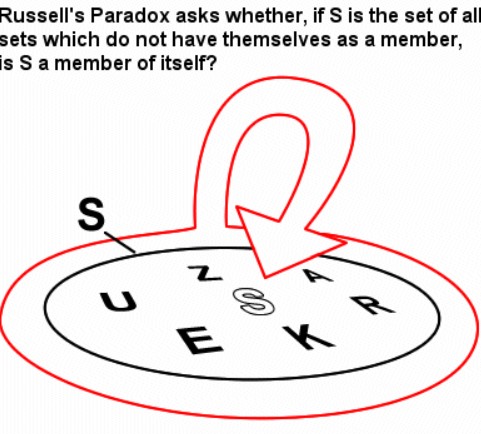
Russell’ın paradoksuna bir yanıt Russell’ın kendisi tarafından Principia Mathematica’da kapsamlı bir tipler sistemi geliştirmesi idi. Bu sistem zahmetli paradokslardan kaçınmasına ve tüm matematiğin tutralı biçimde inşasına izin vermekteydi. Ancak hiçbir zaman geniş çapta kabul görmedi.
İkili Ölümsüz Bir Eser Yaratsa da Çabaları Sonuçsuz Kalacaktı
Sonuç olarak Russell ve Alfred North Whitehead tutarlılığı yeniden sağlamak için Frege’nin projesinin bir çeşidini uygulayarak matematiğin çoğunu kendi tutarlı mantıksal sistemlerine indirgediler. Whitehead’in projedeki rolü, Russell’la birlikte ilk üç cilde ait geniş kapsamlı ayrıntılar üzerinde çalışmaktan ziyade geometrinin mantıksal temelleri olacak olan dördüncü cildin başlıca yazarı olmaktı. Ancak kitabın kalınlığı nedeniyle dördüncü cildi hiç ortaya çıkmadı.

Russell ve Whitehead bu çalışmaları sayesinde dünya çapında ün kazandı. Bu eserden sonra hemen herkes, konuyla ilgilenmeye başlamıştı. Sonucunda da matematiksel mantık büyük bir hızla ilerledi. Ancak 1931 yılında bir Alman bilim dergisinde kısa ve ilgi çekici olduğu kadar da düşündürücü bir yazı yayınlandı. Yazının başlığı şöyleydi. ‘Uber Formal unentscheidbare Sâtze der Principia Mathematica’( Üzerinde kesin kararlar veremeyeceğimiz matematik prensipleri ve benzeri sistemler). Yazarı ise Viyana Üniversitesinden 25 yaşındaki Kurt Gödel idi.

Avusturyalı-Amerikalı mantıkçı, matematikçi Kurt Gödel matematiğin hem tutarlı hem de eksiksiz olamayacağını meşhur eksiklik teoremi ile gösterecekti. ( Detaylar için: Kurt Gödel ve Eksiklik Teoremi: Cevabı Olmayan Sorular Her Zaman Vardır)
Gödel, Öklid zamanından beri uygulanan matematiksel yöntemlerin, doğal sayılar hakkında doğru olan her şeyi keşfetmek için yetersiz olduğunu kanıtladı. Keşfi, 20. yüzyıla kadar matematiğin üzerine inşa edildiği temellerin altını oydu, düşünürleri alternatifler aramaya teşvik etti ve gerçeğin doğası hakkında canlı bir felsefi tartışma yarattı. ( Göz atmak isterseniz: Matematik Felsefesinin Temelini Oluşturan Problemler Nelerdir?)
Kaynaklar ve ileri okumalar
- The 360-Page Proof That 1+1=2. yayınlanma tarihi: Bağlantı: https://www.youtube.com/
- The 300-Page Proof that One Plus One Equals Two. Yayınlanma tarihi: 27 Temmuz 2022; Bağlantı: https://commonplacefacts.com/
- Principia Mathematica 1+1=2; Bağlantı: https://www.storyofmathematics.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel