Bu yazı bir uyarıyla birlikte gelir: Bu sorunu çözmeye uğraşmayınız. İlk bakışta sorunun basitliği ve kolay anlaşılabilir yapısı sizi cezbedebilir. Hatta hemen kağıt ve kalem alıp çözmeyi denemek isteyebilirsiniz. Ancak dikkat! Collatz Problemi, diğer adıyla 3n+1 Problemi, başlangıçta ne kadar sade görünse de, matematikçileri onlarca yıldır meşgul eden çözülmesi zor bir muammadır.
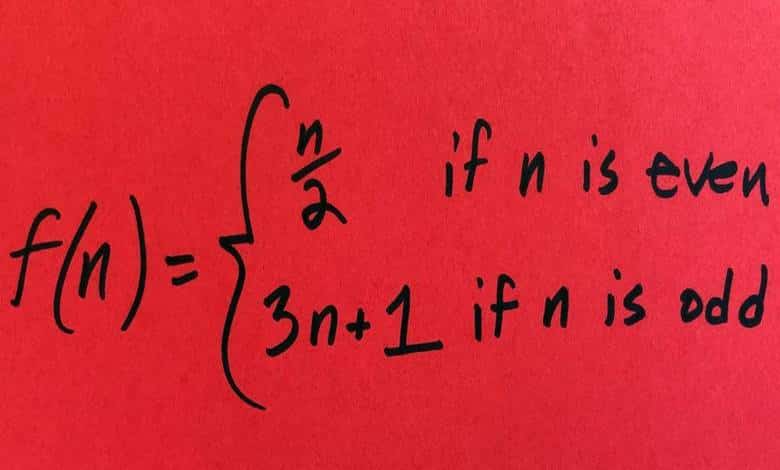
Collatz Problemi Nedir?
1937 yılında Alman matematikçi Lothar Collatz tarafından ortaya atılan bu problem, günümüzde hâlâ çözülememiştir ve matematik dünyasında büyük bir bilinmez olarak kabul edilmektedir. Problem, herhangi bir pozitif tamsayıyla başlayıp belirli bir kurala göre işlem yaparak nihayetinde “1” sayısına ulaşıp ulaşmayacağınızı sorgular.
Olay bu kadar basit gibi görünse de, problemi matematiksel olarak genel bir şekilde kanıtlamak veya çürütmek bugüne kadar mümkün olmamıştır. Collatz Problemi’nin kuralı oldukça basittir: Herhangi bir pozitif tamsayı seçin. Seçtiğiniz sayı üzerinde şu işlemleri uygulayın:
- Eğer sayı çift ise, 2’ye bölün.
- Eğer sayı tek ise, 3 ile çarpıp 1 ekleyin.
- Bu işlemi sonuçlar üzerinde tekrar tekrar uygulayın.
Bu kuralları uyguladığınızda, hangi pozitif tamsayıyla başlarsanız başlayın, sayılar sonunda 4, 2, 1, 4, 2, 1… döngüsüne girer gibi görünmektedir. Örneğin n=5 için 5, 16, 8, 4, 2, 1, 4, 2, 1 şeklinde olacaktır. Benzer biçimde n=11 için, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1. Aşağıdaki örneklerde diğer sayılar için alacağı sonuçları da görebilirsiniz.
Collatz Problemi Aslında Bir Çok Farklı İsimde Karşımıza Çıkar
Bugüne kadar denenen her pozitif tamsayı, sonunda aynı 4, 2, 1 döngüsüne giriyor gibi görünse de, bu durumun her sayı için geçerli olup olmadığını matematiksel olarak kanıtlayabilmiş değiliz. İşte bu nedenle, problem hâlâ bir varsayım olarak anılıyor.
Bu döngüyü ilk fark eden kişi Lothar Collatz oldu. Ancak Collatz, ne varsayımını kanıtlamayı başarabildi ne de bir karşı örnek bulabildi. Hayatı boyunca bu problemle ilgilenmesine rağmen, hakkında kayda değer bir yayın gerçekleştiremedi. Yine de bu basit görünen problem, matematikçiler arasında yayılmaya devam etti ve çözümü olmayan bir bilmece olarak dikkat çekti.
2. Dünya Savaşı sırasında, Polonyalı matematikçi Stanislaw Ulam, bu varsayımı incelemeye başladı. Ulam, boş zamanlarında Collatz Varsayımı üzerinde çalıştı. Ancak ne bir kanıt ne de bir istisna bulabildi. Ulam’ın çalışmaları, problem üzerindeki ilgiyi canlı tuttu ve bu dönemlerde problem, onun adıyla da anılmaya başlandı.
Varsayım, daha sonra Hamburg Üniversitesi’nden sayısal kuramcı Helmut Hasse tarafından ele alındı. Hasse, bu tuhaf problem üzerine Almanya’da ve yurtdışında çeşitli konferanslar verdi. Bu konferanslardan birinde, bir dinleyici bu sayıların hareketlerini dolu tanelerinin yerden zıplamasına benzetti. Bu benzetme, problemi bir süreliğine “Dolu Tanesi Sayıları” ya da İngilizce adıyla Hailstone Dizisi olarak anılmasına yol açtı.
Japon matematikçi Shizuo Kakutani‘nin, problem ile ilgilendiği süreçte de “Kakutani Problemi” olarak da anılmıştı. Ancak ne Collatz, ne Ulam, ne Hasse ne de Kakutani bu problem üzerinde nihai bir sonuca ulaşabilmiştir.
Matematikçiler bu problemi çözmek için yalnızca teorik yöntemlere başvurmadılar; teknolojiden de faydalandılar. Süper bilgisayarlar, Collatz Problemi’ni test etmek için devreye girdi. Bugüne kadar, yaklaşık 300 kentilyon (300 × 10¹⁵) pozitif tamsayı bu varsayımı doğruladı. Tüm bu testler, her bir sayının sonunda 4, 2, 1 döngüsüne ulaştığını gösterdi.
Collatz Problemini Çözmek Mümkün mü?
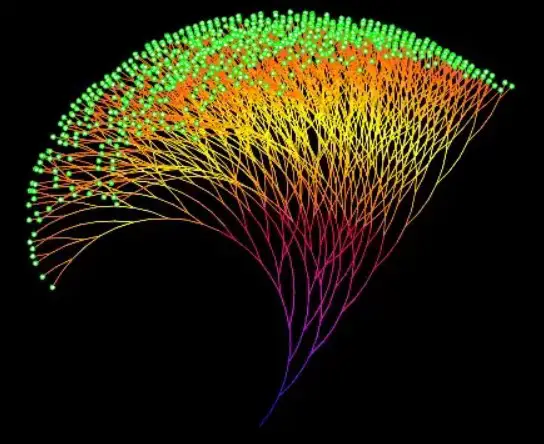
Collatz Problemi’ni çözmek veya anlamak adına matematikçiler, farklı yöntemlerle bu varsayımı analiz etmeye çalıştılar. Grafik çizimler ve modeller oluşturma, bu yöntemlerden biridir. Ancak bu süreçte karşılaşılan en büyük zorluk, problemlerin ardında yatan dinamiklerin bir düzen ve düzensizlik karışımı sergilemesidir.
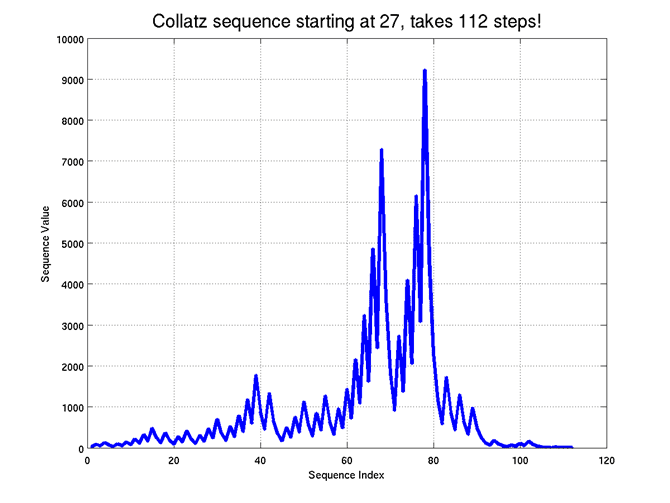
İlk 50 pozitif tamsayı arasında, 1 sayısına geri dönmek için en uzun yolculuğu yapan sayı 27’dir. Bu sayı, tam 112 adımda 1 sayısına ulaşır. Bu süreçte, sayı hem yükselir hem de ani düşüşler yaşar. Grafiksel olarak incelendiğinde, 27 sayısı 67. adımda 7288 değerine ulaşırken, 77. adımda ise 9232 gibi daha da yüksek bir değere çıkar. Ancak bu zirvelerden sonra ani bir çöküş sürecine girer.
Collatz Problemi’nde bazı başlangıç sayıları, sıra dışı uzunlukları ve zirve değerleriyle dikkat çeker. Bu tür sayılara rekortmen sayılar diyebiliriz. Örneğin, başlangıç sayısı 703 olduğunda, Collatz zinciri tam 170 adım sürer ve dizi, 250.504 gibi oldukça yüksek bir zirveye ulaşır.
Başka bir rekortmen sayı olan 26.623, tam 307 adım süren bir zincir oluşturur ve bu süreçte 10.358.020 zirve değerine çıkar. Ancak, bu sayıların da kaçınılmaz sonu, diğer tüm pozitif tamsayılar gibi 1 sayısına ulaşmaktır.
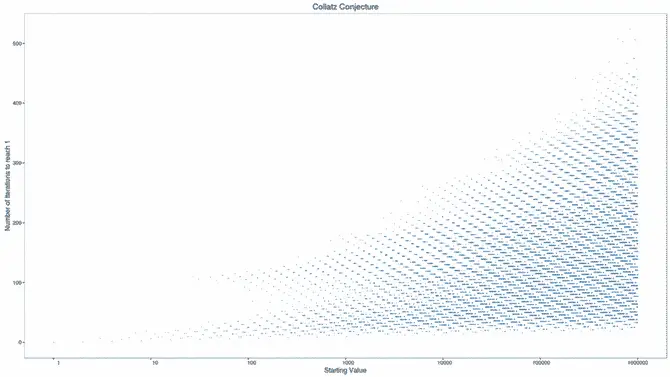
Collatz zincirlerinde, uzunluk ve zirve değeri gibi özelliklerin dağılımı oldukça ilginçtir. Daha büyük sayılar, genellikle daha uzun zincirler oluşturur ve daha yüksek zirvelere ulaşır. Ancak bu durum, her zaman böyle olmaz. Bazı küçük sayılar da oldukça uzun zincirlere ve yüksek zirvelere ulaşacaktır.
Collatz Problemi Çözümsüz Olabilir mi?
Ünlü matematikçi Paul Erdős, Collatz Problemi için bir yorumunda, “Matematik henüz böyle problemlere hazır değil,” demiştir. Bu yorum, problemin ne kadar karmaşık ve derin bir matematiksel meydan okuma olduğunu özetliyor. Ancak bu uyarı, yıllardır matematikçilerin bu probleme çözüm arayışını durdurmamıştır.
2019 yılında, dünyanın yaşayan en büyük matematikçilerinden biri olarak kabul edilen Terence Tao, Collatz Problemi üzerine önemli bir çalışma yayınladı. Tao, problemin çözümü konusunda doğrudan bir kanıt sunamasa da, varsayımı “neredeyse tüm sayılar için neredeyse doğru” olarak tanımlayabilecek bir yöntem geliştirdi. Bu, Collatz Problemi’nin anlaşılmasında önemli bir adım oldu, ancak tam bir çözüm sağlamaktan uzaktı.
Sonucunda Collatz problemi hala çözümsüz. Ayrıca bu varsayımının hiçbir zaman doğru ya da yanlış olduğunu kanıtlayamamamız da mümkündür. Ancak yine de şu anda bir yerlerde yüzlerce kişi bu probleme kafa yormaya devam ediyor.
Belki de siz de onlardan birisinizdir. Esasen matematiğin güzelliği de zaten budur. Yine de hatırlatalım. 268‘den küçük her sayı için bu problem doğrulanmıştır. Dolayısıyla, bir karşı örnek arıyorsanız, yaklaşık 300 kentilyondan başlamalısınız. Bu nedenle denemek isteyenlere şimdiden sabırlar diliyoruz. Yazının devamında göz atmanızı öneririz: Bugüne Kadar Çözülmüş En Zor 9 Matematik Problemi
Kaynaklar ve ileri okumalar:
- The Simplest Math Problem No One Can Solve – Collatz Conjecture. Bağlantı: The Simplest Math Problem No One Can Solve – Collatz Conjecture
- The Simple Math Problem We Still Can’t Solve; yayınlanma tarihi: 23 Eylül 2020; Bağlantı: The Simple Math Problem We Still Can’t Solve/
- Mathematician Proves Huge Result on ‘Dangerous’ Problem; yayınlanma tarihi:11 Aralık 2019; Bağlantı: https://www.quantamagazine.org/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel
