Bilimle ilgilenen ve popüler bilim yayınlarını takip eden hemen herkes Escher’i ve onun eserlerini yakından tanır. Maurits Cornelis Escher ya da kısaca MC Escher (1898–1972) Hollandalı bir grafik sanatçıdır. Escher’in matematik ile ilgili herhangi bir ihtisası yoktur. Ancak çalışmalarında matematiksel kavramları doğru bir şekilde resmetmeyi başarması nedeniyle matematikçiler için son derece önemlidir.

Escher, üçgen, kare, sekizgen gibi temel desenlerden çalışmalarında yararlanır. Sonrasında da onlara yansıma, öteleme ve döndürme yöntemlerini uygulayarak, sayısız çeşitlilikte desen elde eder. Sanatçı, aynı zamanda bu örneklerin özgün biçimlerini bozarak, onları hayvanlara, kuşlara ve diğer başka figürlere dönüştürür.

MC Escher Kimdir?
1898’de dünyaya gelen Escher, Hollanda’da varlıklı bir aile evinde büyüyen beş çocuktan biriydi. Okul hayatını hiç bir zaman fazla sevmedi. İlerleyen süreçte ona bir yön ve amaç duygusu veren sanat tutkusunu keşfetti. Devamında Hollandalı sanatçı Gert Stegeman’ın stüdyosunda çalışmaya başladı.
1919’da Haarlem Mimarlık ve Dekoratif Sanatlar Okulu’nda mimar olmak için eğitime başladı. Sonrasında da öğretmenlerinden birinin cesaretlendirmesiyle, ilgisini mimariden grafik sanatlara kaydırdı. Yirmili yaşlarından başlayarak İtalya ve İspanya’ya yaptığı seyahatler ona ihtiyacı olan ilhamı verdi. Özellikle İspanya’da El Hamra Sarayında bulunan döşemelerin çeşitliliği ve karmaşıklığı, Escher’in mozaiklere olan ilgisini arttırdı.

MC Escher ilerleyen yıllarda Jetta Umiker ile tanışıp aşık oldu ve çift bir yıl sonra evlenip Roma’ya yerleşti ve üç oğulları oldu. İlerleyen süreçte de Escher, Hollanda ve İsviçre’de popüler sergiler düzenlemeye başladı, bu da onun giderek ün kazanmasına neden oldu. Ancak 1930’ların ortalarında MC Escher ve ailesi, faşizmin yükselişinin ardından İtalya’dan kaçtı ve İsviçre’ye taşındı. Escher’in sanatı, bu süre zarfında mozaikli desenlerden sanat ve illüzyon alemlerine doğru kayacaktı.
MC Escher Bir Matematikçi Olmasa da Matematikçileri Büyüleyecekti.
Çalışmaları 1950’lerin başına kadar evrensel olarak dikkat çekmese de,1959’da ilk önemli sergisini açmasıyla, dünya çapında bir üne kavuştu. Hayranlarının büyük bir kısmını, onun çalışmalarının matematik ilkelerin mükemmel bir canlandırması olduğunu fark eden matematikçiler oluşturuyordu. Escher, matematiksel bir yeteneğe sahip olmadığını iddia etse de sonunda matematik ve bilimdeki bir dizi önde gelen ile kendini işbirliği yaparken buldu.

Escher için, çokyüzlü olarak bilinen düzgün katı cisimlerin ayrı bir çekiciliği vardır. Yüzeyleri, tamamen birbirinin aynı olan çokgenlerden şekillere Platonik cisimler denir. Escher bu cisimleri kesiştirerek veya yıldızlaştırarak yani cisimlerinin her bir yüzeyine bir piramit yerleştirerek pek çok ilginç çalışma yapmıştır.


Relativite (1953) isimli çalışması, imkansız bir şekilde birbirine bağlı merdivenlerle çevrili bir binayı tasvir eder. 1954’te bu çalışmayı sergide görme şansı yakalayan matematiksel fizikçi Roger Penrose çizimden çok etkilenmiş devamında imkansız nesneler ile ilgili çalışmalarına başlamıştır.

Escher’in Çalışmalarında Öne Çıkan Matematik
Öklid geometrisi ve Öklid dışı geometrilere ek olarak Escher topolojik şekillerle de yakından ilgilidir. Topolojik şekillere en temel örnek Möbius şerididir, Escher de onu pek çok eserinde kullanmıştır. Möbius şeridi sadece tek bir yüze ve kenara sahiptir. Gerçekten Möbius Şeridi II’deki karıncaların yolunu takip ederseniz, onların aslında farklı yüzeylerde yürümediklerini fark edersiniz.

Bir başka ilgi çekici eser, Resim Galerisi isimli taş baskıdır. Burada, resim galerisinde genç bir adam bir sahil kasabasının ve limanın betimlendiği resmi incelemektedir. Fakat resmin içindeki resim galerisinde de genç bir adam da sahil kasabasının resmedildiği resmi inceler. Genç adam aynı zamanda hem resmin içinde hem de dışında bulunmaktadır.

Escher’in bir başka temel ilgi noktası da perspektiftir. Herhangi bir perspektif çalışmasında, kaçış noktaları, gözün sonsuzdaki noktalar gibi algıladığı noktalar olarak seçilir. Escher aşağıdaki çalışmada beş kaçış noktasına yer verir. Bunun sonucundaki resimde de göreceğiniz gibi algı bozulması yaşanır.

Escher çalışmalarında imkansız nesnelerden de yararlanır. Escher’in bu tür çalışmalarının ilginç örneklerinden biri, Roger Penrose’un imkânsız üçgen düşüncesi üzerine kuruludur. Aşağıda gördüğünüz eserinde iki tane imkânsız üçgen aynı anda kullanılmıştır. Çağlayandan akan su yukarı çıkıp tekrar aşağıya dökülmektedir.

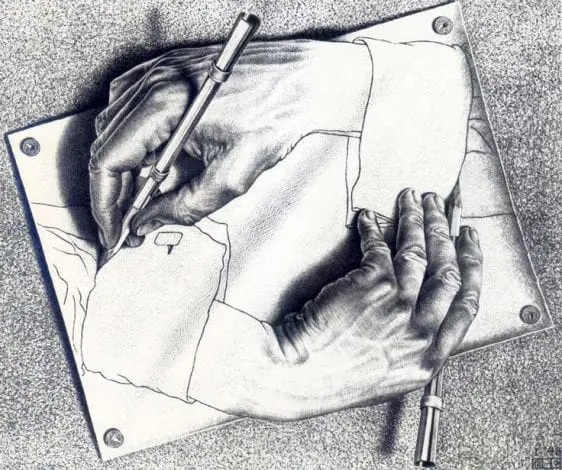
Son olarak Escher’in sanatının, bilgi bilimi ve yapay zekâ alanlarıyla ilişkisinden bahsedebiliriz. Burada Escher’in yakaladığı temel kavram öz gönderge yani kendi kendine referanstır. Çizen Eller isimli çalışmada bunu görebilirsiniz.
Savaş Sonrası Dönem
İlerleyen süreçte sanatının ticari çekiciliği ona Avrupa ve Amerika Birleşik Devletleri’nde uluslararası ün kazandıracaktı. Baskılarına olan talep o kadar yüksekti ki, alıcıları oyalamak için fiyatlarını artırmaya devam etti. Ancak bu hiçbir şey değiştirmedi. Amsterdam’daki dönüm noktası niteliğindeki bir sergiden sonra Escher’in baskıları, matematikçiler Roger Penrose ve HSM Coxeter’in dikkatini çekti. Sonrasında Escher her ikisiyle de karşılıklı olarak yararlı çalışma ilişkileri geliştirecekti.
Daha sonraki yıllarda, Escher, giderek daha karmaşık motiflere sahip matematiksel şekiller ve tasarımlara odaklanacaktı. 1972’deki ölümünden önce yaptığı son büyük sanat eseri olan Snakes, dokuz ayrı, birbirine kenetlenmiş tahta levhadan ve onun kalıcı ve sonsuz yaratıcı icat ruhunu ortaya çıkaran renk unsurlarından oluşuyor.

Escher, uzun yaşamı boyunca, çoğunluğu siyah – beyaz olmak üzere 2000’den fazla çizim ve 448 taşbaskı ve ahşap gravür üretti. Hollanda Lahey’deki Escher in Het Paleis müzesi onun anısına kuruldu
Kaynaklar ve ileri okumalar:
- Lesso, Rosie. “M.C. Escher: Master of the Impossible” TheCollector.com, November 28, 2019, https://www.thecollector.com/
- David Darling and Agnijo Banerjee; At the Edge of the Possible; Oneworld Publications, 2019
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










