Penrose Üçgeni ve Penrose Merdiveni, insan algısını ve görsel illüzyonları anlamak için en etkileyici örneklerden ikisidir. Bu imkansız şekiller, hem sanat hem de bilim dünyasında büyük bir ilgi uyandırmış ve optik yanılsamaların sınırlarını keşfetmeye yönelik çalışmalarda önemli bir yer edinmiştir.

Gözlerimiz bir görüntü algıladığında, beynimiz bu bilgiyi işleyerek bir anlam oluşturur. Ancak, bazen beynimiz gördüğü görüntüyü yanlış yorumlar ve ortaya optik bir illüzyon çıkar. Optik illüzyonlar, beynimize oyun oynayan ve algımızı yanıltan görsellerdir. Işığın, bakış açısının veya görselin çizilme şeklinin etkisiyle, gerçekte orada olmayan şeyleri görmemiz mümkün hale gelir.
Optik illüzyonlar, insan deneyiminin çok eski bir parçasıdır. Modern zamanlarda ise grafik sanatlar ve teknoloji ilerledikçe optik illüzyonların popülaritesi artmıştır. Bu süreç, özellikle 20. yüzyılda “imkansız şekiller” olarak bilinen yeni bir görsel yanılsama türünün ortaya çıkmasına yol açmıştır.
İmkansız Şekiller Nedir?
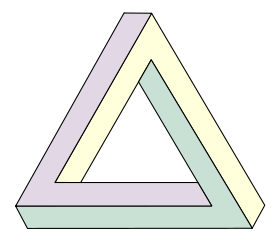
İmkansız şekiller, yalnızca iki boyutlu bir düzlemde var olabilen, ancak fizik kurallarına aykırı oldukları için gerçek dünyada varlığı mümkün olmayan geometrik şekillerdir. Bu şekiller, insan algısının sınırlarını zorlar. Örneğin, Penrose üçgeni olarak bilinen imkansız üçgen, görsel olarak birbirine bağlı bir üçgenin var olduğu algısını yaratır. Ancak bu şekli fiziksel olarak oluşturmak mümkün değildir, çünkü bu durum Öklid geometrisinin temel kurallarını çiğner.
Penrose üçgeninin imkansızlığı, üçgenin kenarlarını oluşturan dikdörtgen prizmaların birbirini 90 derece açılarla kesiyor gibi görünmesinden kaynaklanır. Bu, şeklin görsel açıdan bir bütünlük hissi yaratmasına rağmen fiziksel olarak var olamayacağını ortaya koyar.

Penrose üçgeni, ilk olarak 1934 yılında İsveçli sanatçı Oscar Reutersvärd tarafından tasarlandı. Reutersvärd, fiziksel olarak inşa edilemeyen üç boyutlu şekillerle ilgili çalışmaların öncüsü olmuş ve bu alanda yeni bir sanat formu yaratmıştır. Bu nedenle, kendisi genellikle “imkansız figürlerin babası” olarak anılır.
1950’lerde, psikiyatrist Lionel Penrose ve onun oğlu Nobel ödüllü matematikçi Sir Roger Penrose, bağımsız olarak bu üçgeni yeniden keşfetti. İkili,1958 yılında bu şeklin matematiksel ve psikolojik etkilerini açıklayan bir makale yayınladılar.
Penrose bu üçgeni ilk başlarda üç çubuk olarak isimlendirmişti. Ancak daha sonraları onun adıyla Penrose üçgeni olarak anıldı. Ancak yaygınlaşması Hollandalı grafik sanatçı M. C. Escher’in eserlerinde yer bulmasıyla mümkün olacaktı.
Gerçek Hayatta Penrose Üçgeni Nasıl Görülmektedir?

Penrose üçgeni fiziksel olarak inşa edilemese de, belirli bir açıdan bakıldığında üçgenmiş gibi görünecek şekilde tasarlanabilir. Bu tür optik yanılsamalar, görsel algının nasıl manipüle edilebileceğine dair ilginç örnekler sunar.
Penrose üçgeni üzerine inşa edilen fiziksel modeller, yalnızca belirli bir açıdan bakıldığında üçgen görünür. Perspektif değiştiğinde ise yanılsama bozulacaktır. Escher’in “Şelale” adlı çalışması, Penrose üçgeninin bu ilkesini daha karmaşık bir düzeye taşır.

Çizimde, iki Penrose üçgeni birleştirilerek imkansız bir su döngüsü oluşturulmuştur. Görsel ilk bakışta mantıklı görünse de, suyun döngüsünün fiziksel olarak imkansız olduğu dikkatli bir incelemede anlaşılır.
Bir Başka İmkansız Şekil: Penrose Merdiveni
Penrose üçgeninin bir başka varyasyonu olan Penrose merdiveni, görsel olarak yukarıya veya aşağıya doğru hareket ettiği algısını yaratır. Ancak, bu hareket bir döngü içinde gerçekleşir ve sonuçta başlangıç noktasına geri döner.
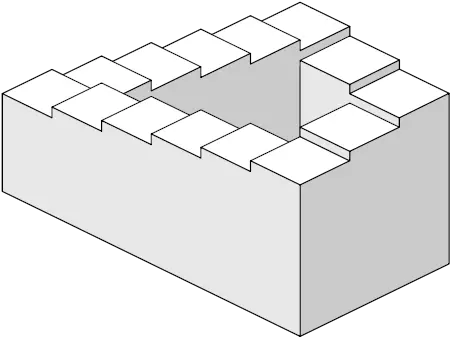
Bu merdiven, gerçek hayatta var olması mümkün olmayan bir şekildir. Penrose merdiveni, Escher tarafından “Çıkanlar ve İnilenler” (Ascending and Descending) adlı çiziminde etkileyici bir şekilde kullanılmıştır. Bu çizimde, aynı yönde hareket eden insanlar hem yukarı hem de aşağı doğru ilerliyor gibi görünür, bu da görsel bir paradoks yaratır.

İmkansız Şekiller ve Popüler Kültür
İmkansız şekiller, yalnızca sanat dünyasında değil, aynı zamanda popüler kültürde de kendine yer bulmuştur. Penrose merdivenleri, 2010 yapımı Başlangıç (Inception) filminde dikkat çekici bir sahnede kullanılmıştır. Filmde, bir karakterin bu merdiven üzerinde sonsuz bir döngüde hareket ettiği gösterilir. 1998 yapımı Yenilmezler (The Avengers) filminde de Penrose merdiveni bir görsel unsur olarak yer almıştır.

Penrose merdivenleri bir çok filmde de yer almıştır. Bunlardan bir tanesi de 2010 yılında çekilen Başlangıç – Inception filmidir. Ayrıca, 1998’deki Yenilmezler filminde de, bir kişinin Penrose merdiveninden aşağı indiği görülmektedir.
İmkansız şekiller, insan algısının sınırlarını ve beynin görsel bilgiyi nasıl işlediğini anlamak için güçlü bir araçtır. Bu şekillerin gerçek dünyada var olamaması, beynimizin gördüklerini nasıl anlamlandırdığına dair önemli ipuçları sunar. Aynı zamanda, yaratıcılığın sınırlarını zorlayan bu eserler, fiziksel gerçekliğin ötesine geçerek, algısal sınırların ötesinde bir dünya yaratır.
Kaynaklar ve ileri okumalar
- Visual curiosities and mathematical paradoxes; yayınlanma tarihi: 17 Kasım 2010; Bağlantı: https://plus.maths.org
- PENROSE LS, PENROSE R. Impossible objects: a special type of visual illusion. Br J Psychol. 1958 Feb;49(1):31-3. doi: 10.1111/j.2044-8295.1958.tb00634.x. PMID: 13536303.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





